LeetCode题练习与总结：被围绕的区域--130

news2024/11/26 10:03:52

一、题目描述

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' 组成，捕获所有 被围绕的区域：

连接：一个单元格与水平或垂直方向上相邻的单元格连接。
区域：连接所有 '0' 的单元格来形成一个区域。
围绕：如果您可以用 'X' 单元格 连接这个区域，并且区域中没有任何单元格位于 board 边缘，则该区域被 'X' 单元格围绕。

示例 1：

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]

输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]

解释：

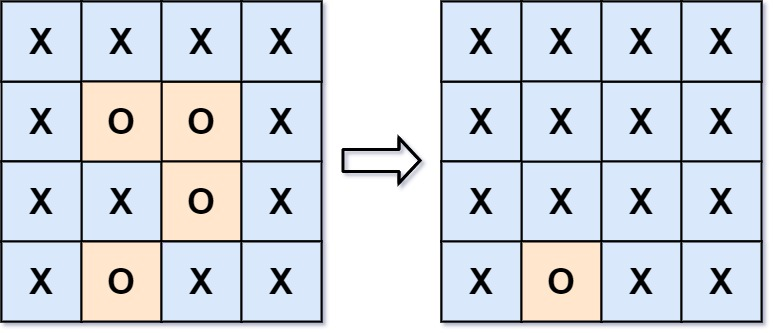
在上图中，底部的区域没有被捕获，因为它在 board 的边缘并且不能被围绕。

示例 2：

输入：board = [["X"]]

输出：[["X"]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 'X' 或 'O'

二、解题思路

这个问题是典型的深度优先搜索（DFS）或并查集（Union-Find）问题。我们可以用DFS来解决这个问题，思路是：

寻找边界上的’O’：首先，我们需要遍历矩阵的边界，找到所有边界上的’O’。
深度优先搜索：从这些边界上的’O’开始，使用DFS将所有与之相连的’O’标记为另一个特殊字符，例如’#‘，表示这些’O’不应被替换为’X’。
替换剩余的’O’：再次遍历整个矩阵，将未被标记为’#‘的’O’替换为’X’。
还原特殊字符：最后，再次遍历矩阵，将所有的’#‘还原为’O’。

三、具体代码

class Solution {
    private int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private int m, n;

    public void solve(char[][] board) {
        if (board == null || board.length == 0) return;

        m = board.length;
        n = board[0].length;

        // Step 1: Find 'O' on the border and start DFS
        for (int i = 0; i < m; i++) {
            dfs(board, i, 0);      // Left border
            dfs(board, i, n - 1);  // Right border
        }
        for (int j = 0; j < n; j++) {
            dfs(board, 0, j);      // Top border
            dfs(board, m - 1, j);  // Bottom border
        }

        // Step 2: Replace 'O' with 'X'
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
        }

        // Step 3: Restore '#' to 'O'
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == '#') {
                    board[i][j] = 'O';
                }
            }
        }
    }

    private void dfs(char[][] board, int i, int j) {
        if (i < 0 || i >= m || j < 0 || j >= n || board[i][j] != 'O') {
            return;
        }
        board[i][j] = '#';
        for (int[] dir : directions) {
            dfs(board, i + dir[0], j + dir[1]);
        }
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

遍历矩阵的边界以寻找’O’并开始DFS的过程，这一步的时间复杂度是O(m+n)，因为矩阵的边界上的单元格总数是m+n。
对每个找到的’O’执行DFS，这一步的时间复杂度是O(m*n)，因为在最坏的情况下，整个矩阵都可能被遍历。
再次遍历矩阵以替换’O’为’X’，这一步的时间复杂度是O(m*n)。
最后，再次遍历矩阵以还原’#‘为’O’，这一步的时间复杂度也是O(m*n)。
综上所述，总的时间复杂度是O(mn)，因为虽然第一步是O(m+n)，但是它相比于后面的O(mn)可以忽略不计。

2. 空间复杂度

DFS的递归调用会使用栈空间，最坏情况下整个矩阵都是’O’，递归的深度将达到mn，因此空间复杂度是O(mn)。

综上所述，代码的时间复杂度是O(mn)，空间复杂度也是O(mn)。

五、总结知识点

二维数组的遍历：代码中多次使用了两层嵌套的for循环来遍历二维数组，这是处理二维数据结构的基本操作。
深度优先搜索（DFS）：dfs函数实现了深度优先搜索算法，这是一种用于遍历或搜索树或图的算法。在这个问题中，DFS用于找到并标记所有与边界上的’O’相连的’O’。
递归：dfs函数是递归的，它自己调用来遍历所有相邻的’O’。递归是一种常用的算法技巧，用于将复杂问题分解为更小的相似问题。
辅助空间的使用：代码中使用了一个二维数组directions来存储四个方向上的移动向量，这有助于在DFS中简化代码。
边界条件检查：在dfs函数中，代码首先检查当前坐标是否越界或者是否是’O’，这是递归的基本安全和正确性保证。
原地修改：代码直接在输入的board数组上进行修改，而不是创建新的数组，这是一种节省空间的做法。
特殊标记和状态转换：代码中使用特殊字符’#‘来标记那些不应该被替换为’X’的’O’，这是一种常见的编程技巧，用于在算法执行过程中保持临时状态。
模拟：整个算法模拟了从一个状态转换到另一个状态的过程，首先标记所有不应该被捕获的区域，然后进行捕获操作，最后恢复标记的区域。