【题目链接】

OpenJudge NOI 2.4 8463:Stupid cat & Doge

【题目考点】

1. 递归

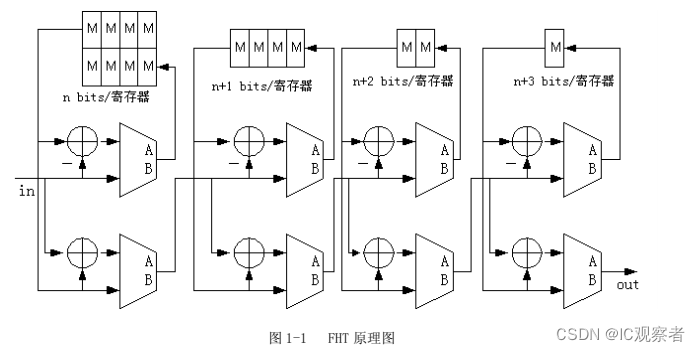
2. 分形图

【解题思路】

解法1：递归

1级正方形边长是$2^1$，2级正方形边长为$2^2$，。。。，n级正方形边长为$2^n$，总格子数量为$2^n\ast 2^n=2^{2n}$，n最大为31，因此房屋（格子）编号最大为$2^{2\ast 31}=2^{62}$，int类型无法保存该数值，需要使用long long类型。（long long类型范围：$-2^{63}\sim 2^{63}-1$)

先假设n级正方形中的每个一级正方形都是开口向左的，也就是图中等级1的样子：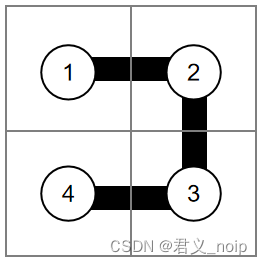
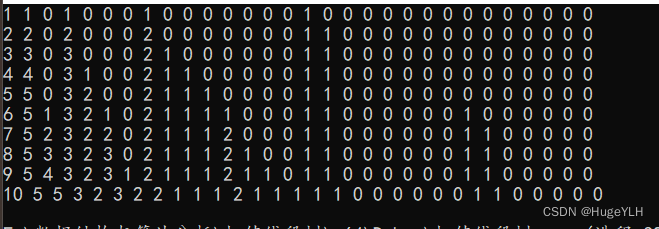
以2级正方形为例，可以先把2级正方形想成如下样子

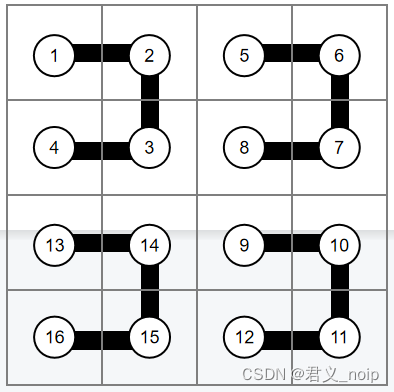
接下来需要做一些转化，才能变为目标图形。

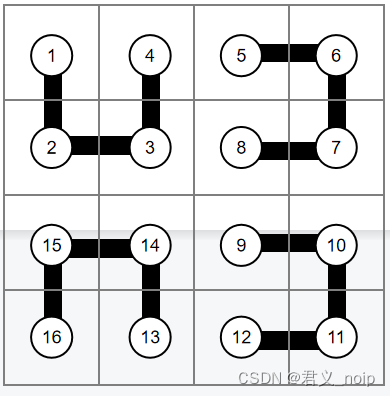
首先左上角需要转成开口向上的图形，按道路行进顺序走第几个格子的位置也随之发生变化。经过观察可知，该变化过程是沿主对角线（左上右下）进行翻转的过程。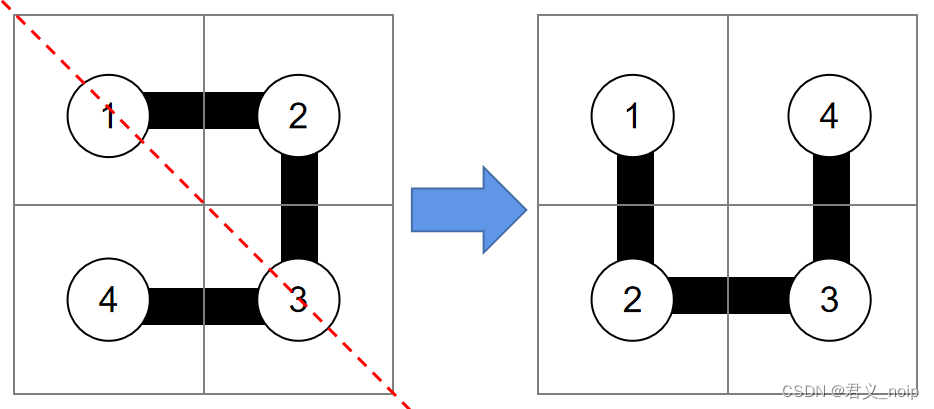

观察主对角线两边对应位置，举出例子

左下方格子	右上方格子
0,0	0,0
1,0	0,1
n-1,0	0,n-1
n-1,1	1, n-1

设结构体

struct Pair
{
    long long x, y;
};

表示一个位置，有Pair p, r，p是翻折前的位置，r是翻折后的位置。
因此该规律也可以表示为r.x = p.y, r.y = p.x

左下需要转成开口向下的图形，按道路行进顺序走第几个格子的位置也随之发生变化。经过观察可知，该变化过程是沿副对角线（右上左下）进行翻转的过程。


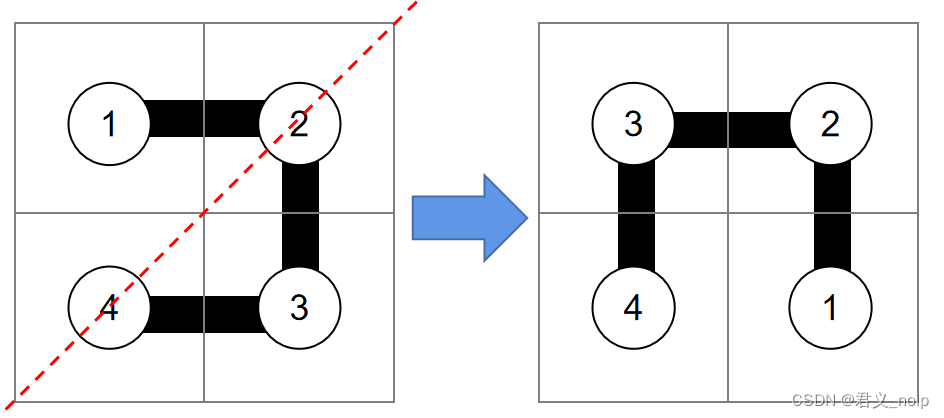
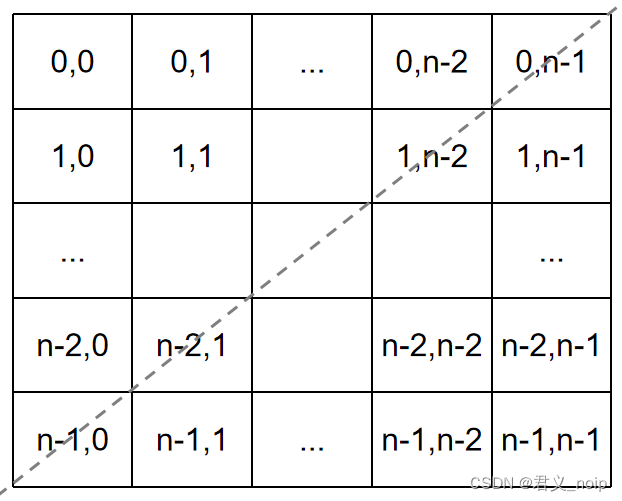
观察副对角线两边对应位置，举出例子

左上方格子	右下方格子
0,0	n-1,n-1
1,0	n-1,n-2
n-1,0	n-1,0
n-2,0	n-1, 1

位置r翻折后是在位置r，观察后得到规律：p.x+r.y = p.y+r.x = n-1
因此关于副对角线翻折r.x = n-p.y-1, r.y = n-p.x-1。

分析递归：
递归问题：在等级n的正方形中找到数值val的位置（等级n的正方形共有$2^{2n}$个格子，格子上的数值分别为$0\sim 2^{2n}-1$，val值的范围也是：$[0,2^{2n}-1]$)
递归关系：
先假设当前等级n的正方形中的4个等级为n-1的小正方形都是开口向左的图形。和1级正方形一样。小正方形编号从0开始数，第0个小正方形在左上方，第1个小正方形在右上方，第2个在右下方，第3个在左下方。
等级n的正方形边长为$2^n$，总格子个数为$2^{2n}$，一共包含4个等级n-1的小正方形，小正方形边长sl为$2^{n-1}$，小正方形的格子个数sn为$2^{2(n-1)}$。
先确定数值val在第几个小正方形中，

第几个小正方形	数值范围
0	[0, sn)
1	[sn, 2*sn)
2	[2*sn, 3*sn)
3	[3*sn, 4*sn)

因此val所在等级n-1的小正方形的编号为：val/sn（整除运算)，在这个小正方形中，要找的数值为val%sn（取模运算）
递归调用该函数，在第val/sn个正方形中找到数值val%sn的位置，为p。
r为调整后在等级为n的大正方形中val的位置。

• 如果val在第0个等级为n-1的小正方形中，那么需要对位置p按照小正方形的主对角线进行翻折，即r.x = p.y, r.y = p.x。
• 如果val在第1个等级为n-1的小正方形中，那么val在右上方的格子中，位置p需要向右移动小正方形边长sl个格子，即r.x = p.x, r.y = p.y+sl
• 如果val在第2个等级为n-1的小正方形中，那么val在右下方的格子中，位置p需要向右和向下分别移动小正方形边长sl个格子，即r.x = p.x + sl, r.y = p.y + sl
• 如果val在第3个等级为n-1的小正方形中，那么需要对位置p先按照小正方形的副对角线进行翻折r.x = n-p.y-1, r.y = n-p.x-1，而后向下移动sl个格子r.x += sl，整合为：r.x = sl-1-p.y+sl, r.y = sl-1-p.x
  返回位置r。

递归出口：如果等级n为0，那么边长只有1，返回位置(0,0)。

根据上述算法写出递归函数Pair find(int n, long long val)，使用该函数，传入猫和狗的房屋编号减一（因为题目给定的房屋编号是从1开始的，我们定义的val是从0开始的），即可求得猫和狗的位置。

得到两只动物的位置后，调用两点间距离公式
$dis(a,b)=\sqrt{(a.x-b.x{)}^2+(a.y-b.y{)}^2}$，乘上单位“10米”，再四舍五入取整，即可得到最终结果。
【注意】四舍五入取整，可以使用printf("%.0f", a)来完成，或者自己写取整函数

long long myRound(double a)
{
	return a+0.5;//返回时自动强转为long long
}

都可以。
该题惟独不能用<cmath>中的round()函数！！！，用了就报错，我也不知为什么。

【题解代码】

解法1：递归

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
struct Pair
{
    LL x, y;
    Pair(){}
    Pair(LL a, LL b):x(a), y(b){}
};
Pair find(int n, LL val)//在等级n的正方形中查找数值val的位置。val的值为0~2^(2*n)-1
{
    if(n == 0)
    	return Pair(0,0);
    LL sl = 1 << (n-1), sn = sl*sl;//sl:小正方形边长2^(n-1) sn:小正方形的元素个数
	Pair p = find(n-1, val%sn), r;//val%sn:在小正方形中的数值 p:val在小正方形中的位置 r:val在大正方形中的位置
    switch(val/sn)//val/sn:val在第几(0,1,2,3)个小正方形中
    {
        case 0://关于主对角线轴对称
        	r.x=p.y, r.y=p.x;
        	break;
        case 1://左上平移到右上
        	r.x = p.x, r.y = p.y + sl;
        	break;
        case 2://左上平移到右下
        	r.x = p.x + sl, r.y = p.y + sl;
        	break;
        case 3://关于副对角线轴对称 p.x+r.y=p.y+r.x=sl-1，再向下移动sl,
        	r.x = sl-1-p.y+sl, r.y = sl-1-p.x;
        	break;
    }
    return r;
 }
double getDis(Pair a, Pair b)
{
     return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
LL myRound(double a)
{
	return a+0.5;//返回时强转为LL 
}
int main()
{
    LL t, n, s, d;//注意：s, d必须声明为LL 
    cin >> t;
    while(t--)
    {
        cin >> n >> s >> d;
        Pair pCat = find(n, s-1), pDog = find(n, d-1);
        cout << myRound(getDis(pCat, pDog)*10) << endl;//注意，不能用<cmath>中的round函数，用了就报错。
    }
    return 0;
}