这是一道简单的数学题。但是比较繁琐,需要有耐心。
目录
前言
一、找规律
二、怎么实现加法?
总结
前言
这道题不让用四则运算符做加法,于是我第一反应是用位运算。
难道转成二进制再使用位运算吗,显然不需要,列草稿可以观察到一部分规律。
一、找规律
列出5+7的二进制竖式,可以得知:
两数相加分为本位和与进位和,本位和是按位异或的结果,进位和是按位与的结果,进位需要进在上一位,所以需要左移。

二、怎么实现加法?
将本位和与进位(左移一位后的)进行按位异或,这样可以得到两个数字本位和与进位的无进位之和,接着本位和与进位进行按位异或和按位与分别求出他们的本位和与无进位和。
举个例子:
现有两数a = 5, b = 7:a = 0101, b = 0111,
a ^ b = 0010得到 a 与 b 的无进位之和 sum = 0010;
a & b = 0101得到 a 与 b 的进位,左移一位后得到真正的进位add = 1010;
sum ^ add = 1000得到第一次进位后的无进位和,保存在 a 中,此时a = 1000;
sum & add = 0010得到第一次进位后的进位,左移后保存在 b 中,此时b = 0100;
由进位0100可知现在仍有进位没有被进上去,重复上述过程:
a ^ b = 1100得到 a 与 b 的无进位之和 sum = 1100;
a & b = 0000得到 a 与 b 的进位,此时说明进位以进完, add = 0000;
sum ^ add = 1100得到第二次进位后的无进位和,保存在 a 中,此时a = 1100;
进位为0,结束循环,返回 a 为和。
代码如下(示例):
#include <stdio.h>
int main()
{
int num1 = 53;
int num2 = 17;
while (num2 != 0)
{
// 无进位和
int sum = num1 ^ num2;
// 进位
int add = (num1 & num2) << 1;
num1 = sum ^ add;
num2 = (sum & add) << 1;
}
printf("%d", num1);
return 0;
}总结
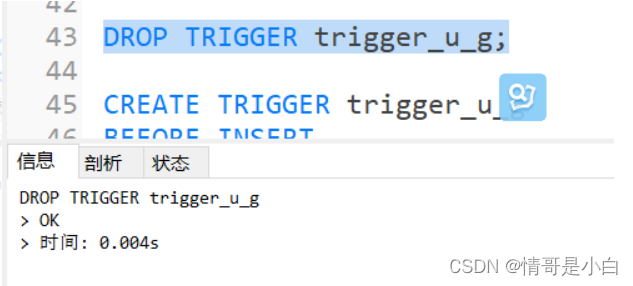
进行位运算是一项细心的活,需要我时刻保持清醒的大脑去进行运算,像小学一年级那样,一步一步,不能有任何疏忽和马虎,在编程这件事上,我也正好是一年级。








![单链表的使用方法.数据结构(三)[上]](https://img-blog.csdnimg.cn/e1a54182c2934052ba201d0d103ec7d5.jpeg)