1、关系代数概述

关系代数是一种抽象的查询语言，是关系数据操纵语言的一种传统表达方式，它是利用对关系的运算来表达查询的。

任何运算都是将一定的运算符作用于一定的运算对象上，得到预期的运算结果。

关系代数的运算对象是关系，运算结果亦为关系。

运算符：

• 集合运算符
  • 将关系看成元组的集合
  • 从关系的“水平”方向即行的角度来进行运算
• 专门的关系运算符
  • 不仅涉及行而且涉及列
• 算术比较符
  • 辅助专门的关系运算符进行操作
• 逻辑运算符
  • 辅助专门的关系运算符进行操作

常见的关系运算符如下：

1.1 传统的集合运算

设关系$R$和关系$S$是相容的，$t$代表元组变量，现将各种运算分别介绍如下：

（1）并（Union）

• 关系$R$与关系$S$的并记作： R ∪ S = { t ∣ t ∈ R ∨ t ∈ S } R∪S=\{t|t∈R∨t∈S \} R∪S={t∣t∈R∨t∈S}
• 结果关系是由属于$R$或属于$S$的元组组成，且结果仍为$n$目关系，但结果关系要消除重复元组。

举例：

$R$和$S$

• 具有相同的目$n$（即两个关系都有n个属性）
• 相应的属性取自同一个域

$R\cup S$

• 仍为$n$目关系，由属于$R$或属于$S$的元组组成
  • R ∪ S = { t ∣ t ∈ R ∨ t ∈ S } R∪S=\{t|t∈R∨t∈S \} R∪S={t∣t∈R∨t∈S}

具体如下图所示：

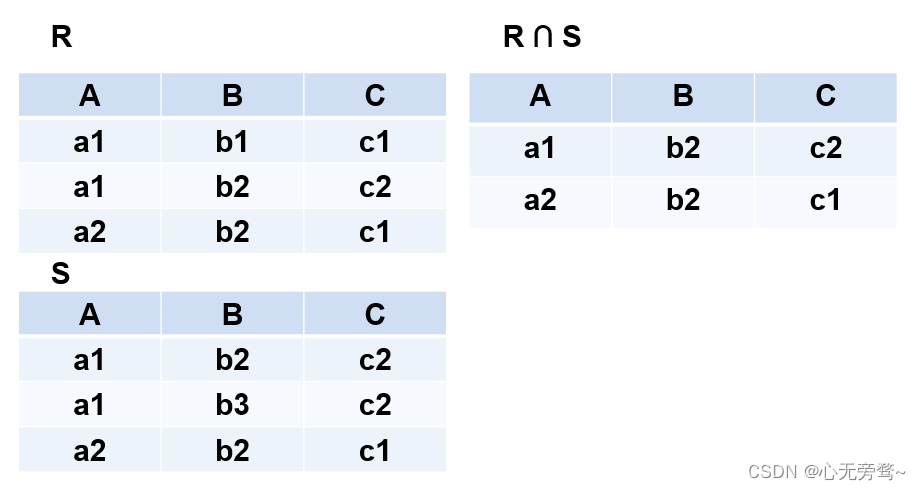
（2）交（ Intersection）

• 关系$R$与关系$S$的交记作： R ∩ S = { t ∣ t ∈ R ∧ t ∈ S } R∩S=\{t|t∈R∧t∈S \} R∩S={t∣t∈R∧t∈S}
• 结果关系由既属于$R$又属于$S$的元组组成，且仍为$n$目关系。

举例：

$R$和$S$

• 具有相同的目$n$
• 相应的属性取自同一个域

$R\cap S$

• 仍为$n$目关系，由既属于$R$又属于$S$的元组组成
  • R ∩ S = { t ∣ t ∈ R ∧ t ∈ S } R∩S=\{t|t∈R∧t∈S \} R∩S={t∣t∈R∧t∈S}

具体如下图所示：

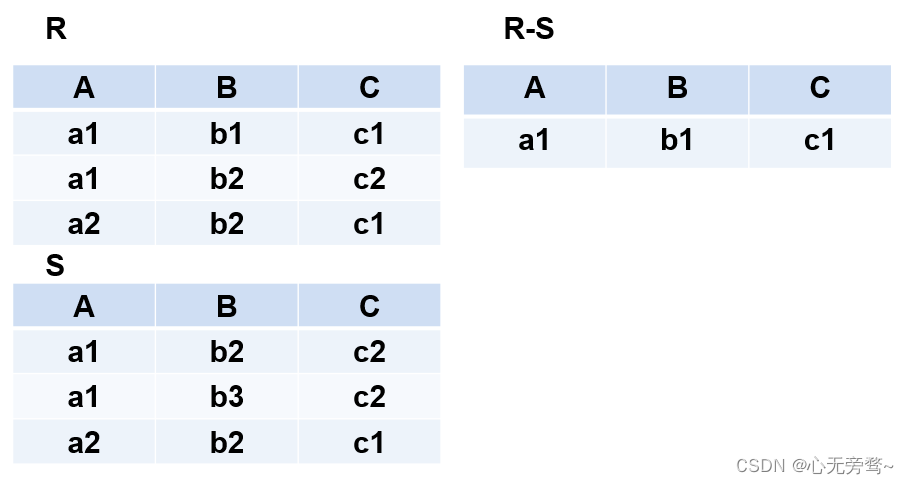
（3）差（Difference）

• 关系R与关系S的差记作： R − S = { t ∣ t ∈ R ∧ t ∉ S } R-S=\{t|t∈R ∧t \notin S\} R−S={t∣t∈R∧t∈/S}
• $R$和$S$的差，结果关系由属于$R$而不属于$S$的所有元组组成，且仍为$n$目关系,即在关系$R$中减去$R$和$S$的相同元组。

举例：

$R$和$S$

• 具有相同的目$n$
• 相应的属性取自同一个域

$R-S$

• 仍为$n$目关系，由属于$R$而不属于$S$的所有元组组成
  • R − S = { t ∣ t ∈ R ∧ t ∉ S } R-S=\{t|t∈R ∧t \notin S\} R−S={t∣t∈R∧t∈/S}

（4）广义笛卡尔积（Extended Cartesian Product）

• 两个分别为 $n$目和$m$目的关系，$R$和$S$的广义笛卡尔积是一个$(n+m)$列的元组的集合。
• 元组的前$n$列是关系$R$的一个元组，后$m$列是关系$S$的一个元组。若$R$有$k_1$个元组，$S$有$k_2$个元组，则关系$R$和关系$S$的广义笛卡尔积有$k_1\times k_2$个元组。
• 记作：$R\times S=\{(a_1,a_2,\dots a_m,b_1,b_2,\dots b_n)|(a_1,a_2,\dots a_m)\in R\wedge (b_1,b_2,\dots b_n)\in S\}。$

严格地讲应该是广义的笛卡尔积

• $R$: $n$目关系，$k_1$个元组
• $S$: $m$目关系，$k_2$个元组

$R\times S$

• 列:$m+n$列元组的集合

  • 元组的前$n$列是关系$R$的一个元组
  • 后$m$列是关系$S$的一个元组

• 行：$k_1\times k_2$个元组
  
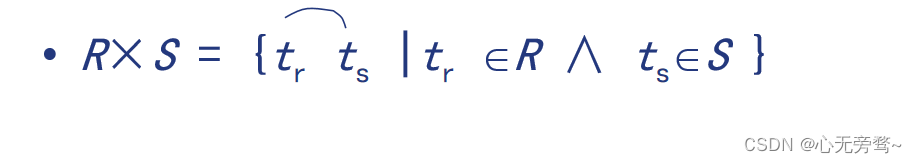
  具体如下图所示：
  

1.2 专门的关系运算

在讲解之前，我们先引入几个记号，这样有助于下面的理解，确实关系代数后半部分有点难理解。
（1）$R,t\in R,t[A_i]$
设关系模式为$R(A_1，A_2，\dots ，A_n)$，它的一个关系设为$R$，$t\in R$表示$t$是$R$的一个元组，$t[A_i]$则表示元组t中相应于属性$A_i$的一个分量。

（2）$\overbrace{t_r{t}_s}$ ， $R$为$n$目关系，$S$为$m$目关系。
$t_r\in R，t_s\in S，\overbrace{t_r{t}_s}$称为元组的连接。$\overbrace{t_r{t}_s}$是一个$n+m$列的元组，前$n$个分量为$R$中的一个$n$元组，后$m$个分量为$S$中的一个$m$元组。
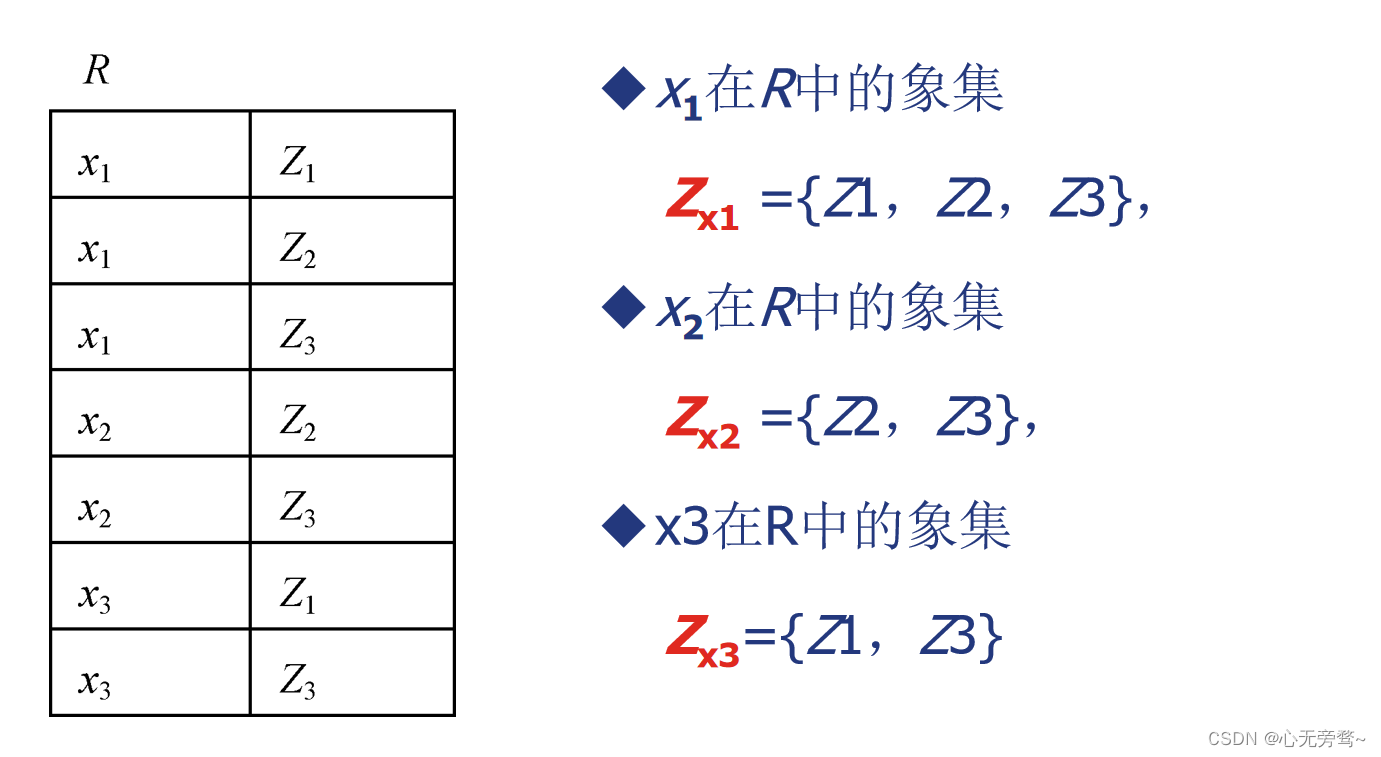
（3）象集$Z_x$
给定一个关系$R（X,Z）$，$X$和$Z$为属性组。当$t[X]=x$时，$x$在$R$中的象集（Images Set）为：
$$Z_x=t[Z]|t\in R，t[X]=x$$

它表示$R$中属性组$X$上值为$x$的诸元组在$Z$上分量的集合。

举例如下：

上面抽象的例子可能并不是特别容易理解，那么我们就拿生活中的实际例子进行解释：

学生-课程-选修关系:
学生关系Student、课程关系Course和选修关系SC

在上面的关系表中，我们可以把SC表看作一个关系R，它的属性组为学号，课程号以及成绩，即$R(Sno,Cno,Grade)$。这时我们将SC表与上面那个例子对比可以看出，Sno为200215121的学号在关系R（SC表）中的象集为 S n o 200215121 = { 1 ， 2 ， 3 } Sno_{200215121}=\{1，2，3\} Sno200215121​={1，2，3}，以此类推，这样就比较容易理解一点。

1.2.1 选择运算

• 选择又称为限制
• 选择运算符的含义
  • 关系R上的选择操作是根据某些条件对关系R做水平分割，即从行的角度选择符合条件的元组。
• 在关系R中选择满足给定条件的诸元组
  • 记作： σ F （ R ） = { t ∣ t ∈ R ∧ F ( t ) = ‘真’ } σF（R）=\{t|t∈R∧F(t)=‘真’\} σF（R）={t∣t∈R∧F(t)=‘真’}
• F：选择条件，是一个逻辑表达式，取逻辑值“真”或“假”。
• 选择运算是从关系R中选取使逻辑表达式F为真的元组，是从行的角度进行的运算

F：选择条件，是一个逻辑表达式

• 基本形式为：$X_1\theta Y_1$
• $\theta$：比较运算符$（＞，\ge ，＜，\le ，＝或<>）$
• $X_1，Y_1$：属性名、常量、简单函数.
• 属性名也可以用它的序号来代替；

以最上面的学生-课程-选修关系表举例说明更好理解：

[例1] 查询信息系（IS系）全体学生

${\sigma }_{Sdept}{=}^{\prime }I{S}^{\prime }(Student)或{\sigma }_5{=}^{\prime }I{S}^{\prime }(Student)$

结果：

[例2] 查询年龄小于20岁的学生
${\sigma }_{Sage<20}(Student)或{\sigma }_{4<20}(Student)$

结果：

1.2.2 投影（Projection）

投影运算符的含义：

• 从R中选择出若干属性列组成新的关系
  • ${\pi }_A(R)=t[A]|t\in R$
  • A：R中的属性列

投影操作主要是从列的角度进行运算：

但投影之后不仅取消了原关系中的某些列，而且还可能取消某些元组（避免重复行）

举例说明一下：
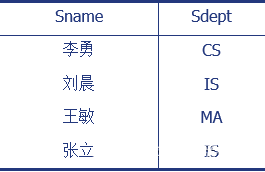
[例3] 查询学生的姓名和所在系
即求Student关系上学生姓名和所在系两个属性上的投影

${\pi }_{Sname，Sdept}(Student)或{\pi }_{2，5}(Student)$

结果：

[例4] 查询学生关系Student中都有哪些系

${\pi }_{Sdept}(Student)$

结果：

由此可见，使用投影操作可以将关系表中的列单独拿出来组成新的关系表，这样方便我们可以更加清楚的查看自己想要的信息。

1.2.3 连接（Join）

连接也称为$\theta$连接

连接运算的含义：
从两个关系的笛卡尔积中选取属性间满足一定条件的元组

连接运算从$R和S$的广义笛卡尔积$R\times S$中选取（$R$关系）在$A$属性组上的值与（$S$关系）在$B$属性组上值满足比较关系$\theta$的元组

举例说明一下：
[例5]关系R和关系S 如下所示：

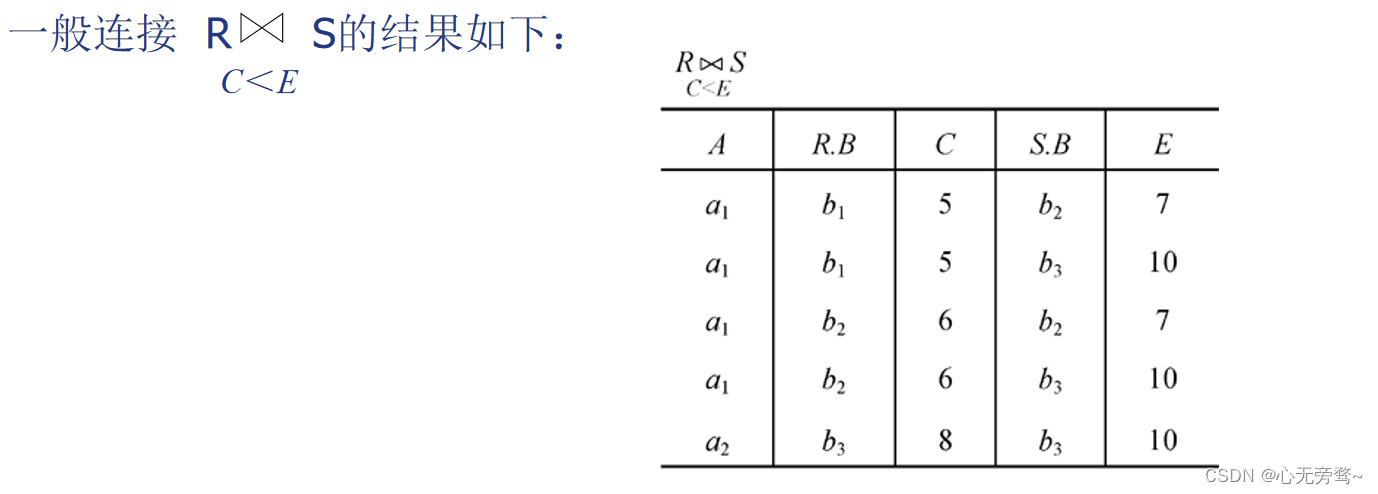
1.2.4 两类常用连接运算

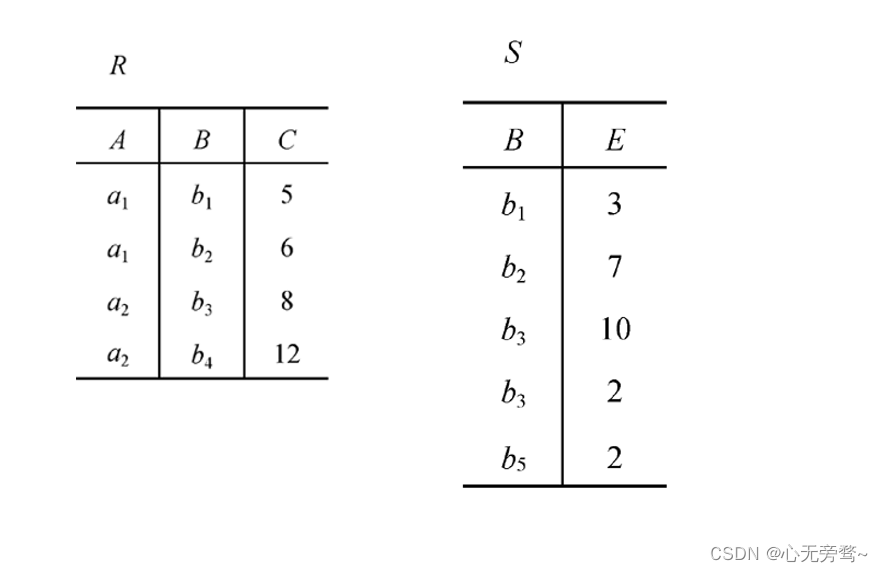
（1）等值连接（equijoin）

• 什么是等值连接?
  • θ为“＝”的连接运算称为等值连接
• 等值连接的含义
  • 从关系R与S的广义笛卡尔积中选取A、B属性值相等的
    那些元组，即等值连接为：
    
    举例说明：
    
    
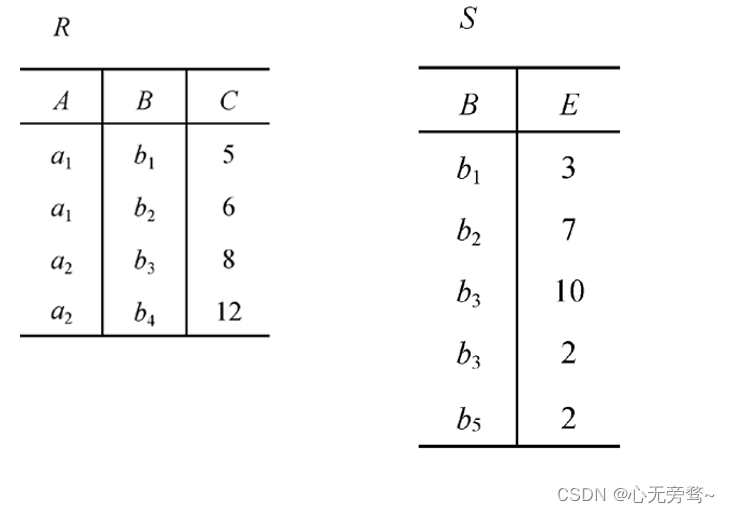
    （2）自然连接（Natural join）
• 自然连接是一种特殊的等值连接
  • 两个关系中进行比较的分量必须是相同的属性组
  • 在结果中把重复的属性列去掉
• 自然连接的含义
  • R和S具有相同的属性组B

举例：


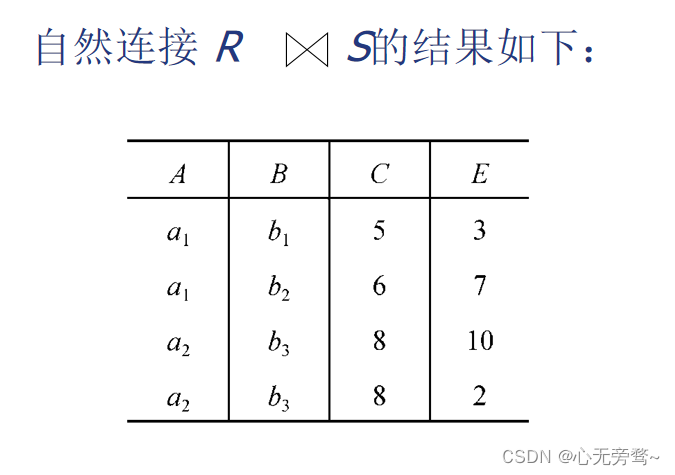
一般的连接操作是从行的角度进行运算。

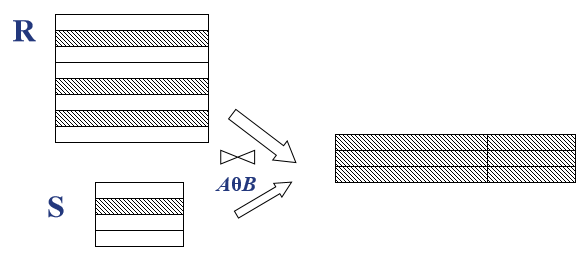
自然连接还需要取消重复列，所以是同时从行和列的角度进行运算。

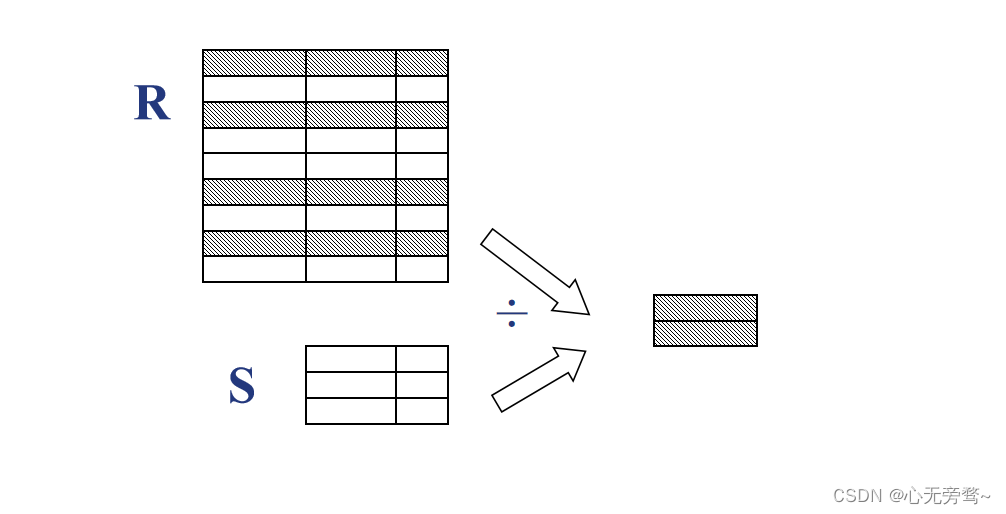
1.2.5 除（Division）

给定关系$R(X，Y)$和$S(Y，Z)$，其中$X，Y，Z$为属性组。$R$中的$Y$与$S$中的$Y$可以有不同的属性名，但必须出自相同的域集。$R$与$S$的除运算得到一个新的关系$P(X)$，$P$是$R$中满足下列条件的元组在 $X$ 属性列上的投影：

元组在$X$上分量值$x$的象集$Y_x$包含$S$在$Y$上投影的集合，记作：

关于象集的概念我们在前面已经提到了，在此直接举例子说明除：

[例6]设关系$R、S$分别为下图的(a)和(b)，$R÷S$的结果为图©

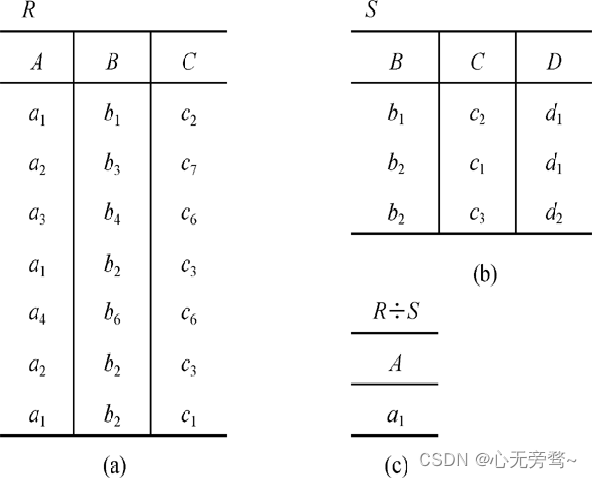
通过上面的结果我们可以发现，关系$R$中的$B、C$属性组，和关系$S$中的$B、C$属性组的域都是相同的，$R与S$的除运算得到了一个新的关系，我们将它当做$P(A)$，$P$是$R$中满足上述条件的元组在$A$属性列中的投影。

分析：
设关系$R，S$,分别为例6中的(a)和(b)，$R÷S$的结果为图©,关系$R$中$A$可以取四个值 { a 1 ， a 2 ， a 3 ， a 4 } , \{ a_1，a_2，a_3，a_4\}, {a1​，a2​，a3​，a4​}, 其中：

• $a_1$的象集为 { （ b 1 ， c 2 ） , （ b 2 ， c 1 ），（ b 2 ， c 3 ） } \{（b_1，c_2）,（b_2，c_1），（b_2，c_3）\} {（b1​，c2​）,（b2​，c1​），（b2​，c3​）}
• $a_2$的象集为 { （ b 3 ， c 7 ） , （ b 2 ， C 3 ） } \{（b_3，c_7）,（b_2，C_3）\} {（b3​，c7​）,（b2​，C3​）}
• $a_3$的象集为$\{(b_4，c_6)\}$
• $a_4$的象集为 { （ b 6 ， c 6 ） } \{（b_6，c_6）\} {（b6​，c6​）}

$S$在$（B，C）$上的投影为 { （ b 1 ， c 2 ），（ b 2 ， c 1 ） , （ b 2 ， c 3 ） } \{（b_1，c_2），（b_2，c_1）,（b_2，c_3）\} {（b1​，c2​），（b2​，c1​）,（b2​，c3​）}

显然只有$a_1$的象集包含了$S$在$(B,C)$属性组上的投影，所以 R ÷ S = { a 1 } R÷S=\{a1\} R÷S={a1}。

除操作是同时从行和列角度进行运算

📢博客主页：https://blog.csdn.net/m0_63007797?spm=1011.2415.3001.5343
📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正！
📢本文由 心无旁骛~ 原创，首发于 CSDN博客🙉
📢停下休息的时候不要忘了别人还在奔跑，希望大家抓紧时间学习，全力奔赴更美好的生活✨