目录
- 1.算法原理
- 2.改进点
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.算法原理
【智能算法】蜜獾算法(HBA)原理及实现
2.改进点
限制反向学习机制
在挖掘模式和蜂蜜模式不同路径更新的基础上引入限制反向学习机制,在算法迭代时,对当前的种群个体进行限制反向学习,生成新的限制反向解,提升解的质量,增加种群多样性,加快算法收敛速度:
x
ˉ
i
=
r
r
a
n
d
×
(
u
u
b
+
l
l
b
−
x
i
)
(1)
\bar{x}_{i}=r_{\mathrm{rand}}\times \left( u_{\mathrm{ub}}+l_{\mathrm{lb}}-x_{i} \right)\tag{1}
xˉi=rrand×(uub+llb−xi)(1)
其中,参数表述为:
u
u
b
=
max
(
x
i
)
,
l
l
b
=
min
(
x
i
)
(2)
u_{\mathrm{ub}}=\max\left( x_{i} \right),l_{\mathrm{lb}}=\min\left( x_{i} \right)\tag{2}
uub=max(xi),llb=min(xi)(2)
限制反向学习机制相比于反向学习,解的上下限随迭代次数变化且限制了反向解越过边界。相比反向学习机制,限制反向学习机制进一步优化种群质量,使得在增加种群多样性的基础上,加快了算法的收敛速度。
自适应权重因子
捕猎过程中猎物目标对蜜獾位置更新的影响以及自适应权重因子可有效平衡算法在不同阶段的搜索能力:
ω
=
tan
(
t
t
max
)
(3)
\omega=\tan\left(\frac{t}{t_{\max}}\right)\tag{3}
ω=tan(tmaxt)(3)
加入自适应权重因子能够促进算法全局和局部搜索平稳过渡。
饥饿搜索策略
当蜜獾表现出能量较低、适应度较差时,蜜獾处于饥饿状态,通过改变蜜獾的寻优路径增强搜索能力,从而避免算法陷入局部最优:
x
n
e
w
=
x
p
r
e
y
×
ω
+
F
1
×
α
×
d
i
×
r
7
×
exp
(
x
w
o
r
s
e
−
x
i
)
(4)
x_{\mathrm{new}}=x_{\mathrm{prey}}\times\omega+F_{1}\times\alpha\times d_{i}\times r_{7}\times\exp(x_{\mathrm{worse}}-x_{i})\tag{4}
xnew=xprey×ω+F1×α×di×r7×exp(xworse−xi)(4)
3.结果展示
CEC2005
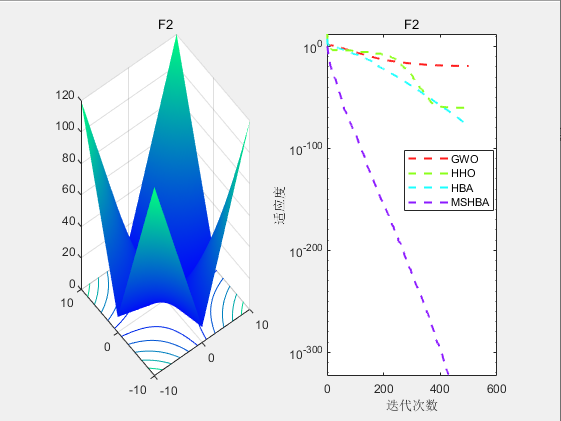
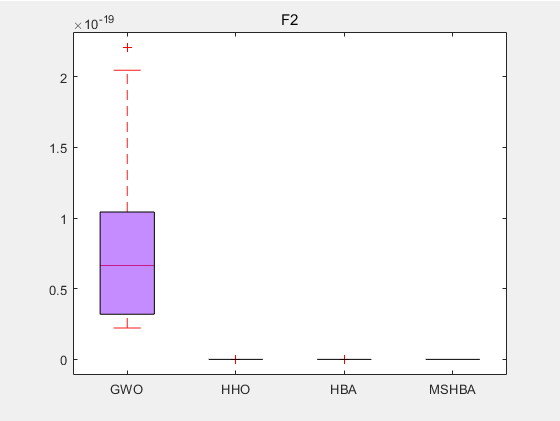
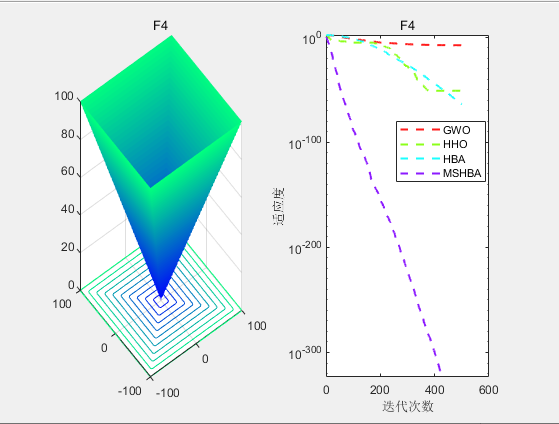
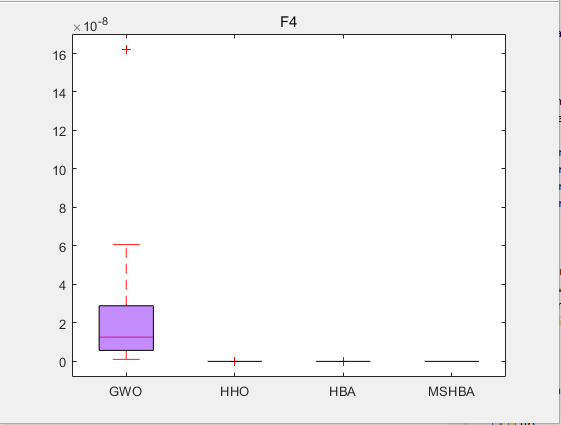
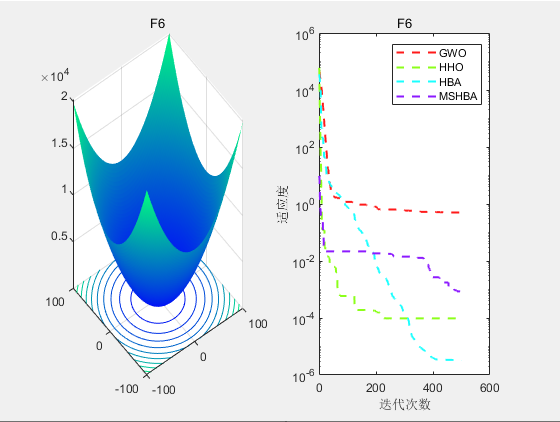
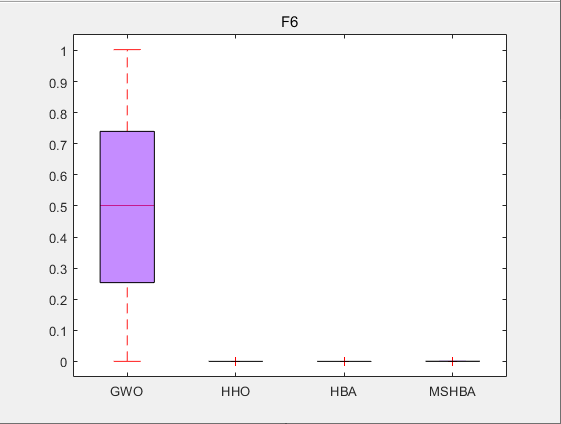
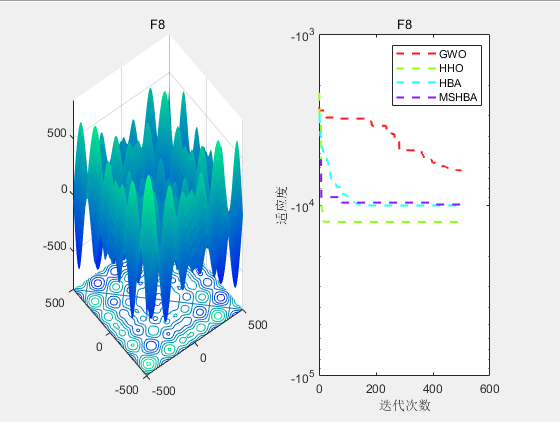
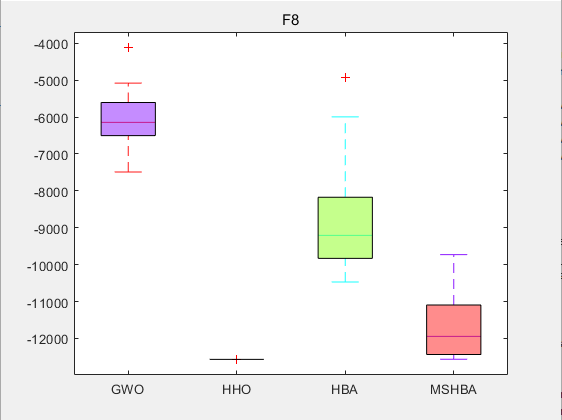
4.参考文献
[1] 向海昀,李鸿鑫,符晓,等.基于多策略的改进蜜獾算法及其应用[J].计算机工程,2023,49(12):78-87.









![【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 任务积分优化问题(100分) - 三语言AC题解(Python/Java/Cpp)](https://img-blog.csdnimg.cn/direct/81e5025eb00c4000b154f2756187269b.png)