python数据分析--- ch11 python数据描述性统计
- 1. Ch11--描述性统计
- 2. 数据集中趋势的度量
- 2.1 平均值
- 2.2 中位数
- 2.3 众数
- 2.4 几何平均值
- 2.5 调和平均值
- 3. 数据离散趋势的度量
- 3.1 极差
- 3.2 平均绝对偏差(MAD)
- 3.3 方差和标准差
- 3.4 下偏方差和下偏标准差
- 3.5 目标下偏方差和目标下偏标准差
- 4. 峰度、偏度与正态性检验
- 4.1 偏度
- 4.2 峰度
- 4.3 正态性检验
- 4.3.1 Jarque-Bera(大样本)
- 4.3.2 $ D'Agostino's K^2$ 检验(中小样本)
- 4.3.3 Shapiro-Wilk 检验(小样本)
- 4.3.4 Kolmogorov-Smirnov (K-S) 检验
- 4.3.5 Anderson-Darling 检验
- 4.3.6 Q-Q图和P-P图
- 5. 异常数据识别与处理
- 5.1 初始数据查看
- 5.2 固定比例法
- 5.3 均值标准差法
- 5.4 MAD法
- 5.5 Boxplot法
1. Ch11–描述性统计
描述性统计工具用于总结和组织数据,提供数据的中心趋势、分布和形状的度量。
-
使用场景: 当需要快速了解数据集的基本特征时。
-
功能: 计算均值、中位数、方差、标准差等。
Python描述性统计工具
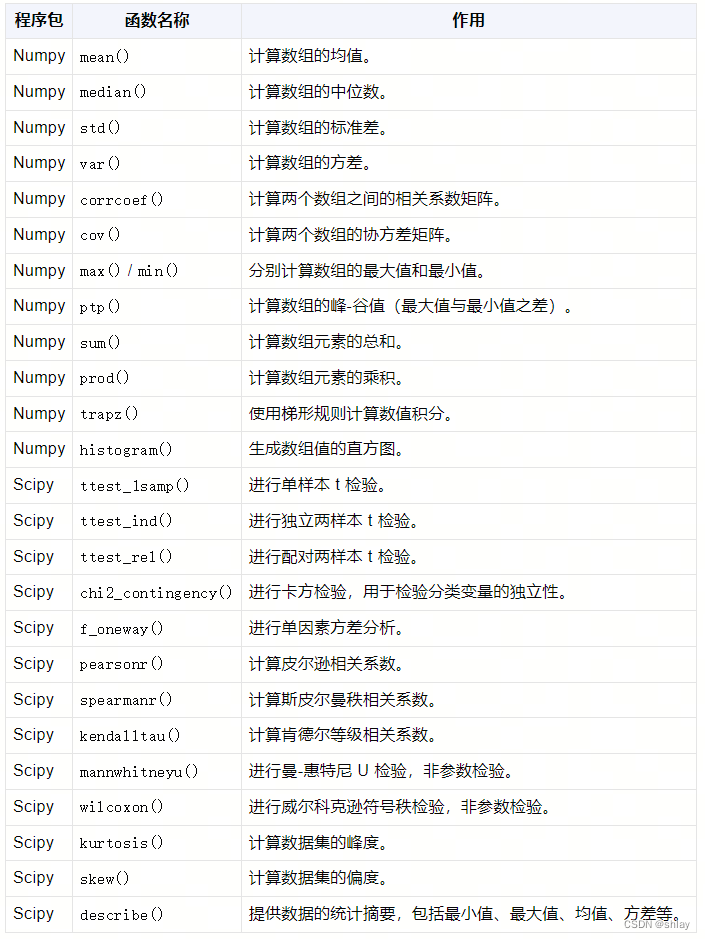
Pandas 是一个强大的 Python 数据分析工具库,它提供了一系列用于数据分析和操作的函数。以下是一些常用的 Pandas 统计方法的整理表格,列出了函数名称及其作用:
Numpy 和Scipy包常用的统计方法:
2. 数据集中趋势的度量
集中趋势的度量包括均值、中位数和众数等,它们提供了数据的中心位置。
- 使用场景: 分析数据的中心点。
- 功能: 计算数据的均值、中位数、众数等。

在上表中:
- 𝑥𝑖表示数据集中的第 𝑖 个观测值。
- 𝑛表示数据集中观测值的总数。
- 𝑤𝑖表示观测值𝑥𝑖相应的权重。
- 𝑓(𝑥)表示数据集中各值出现的频率。
请注意,上表中提供的公式用于解释度量计算的基本原理,实际的库函数可能会采用不同的实现方法。例如,NumPy 的 mean() 函数可以直接计算算术平均值,而加权算术平均值可能需要用户手动实现,或者使用 SciPy 中的 average() 函数,该函数允许指定权重。
对于几何平均值和调和平均值,NumPy 和 SciPy 没有直接提供计算函数,但它们可以通过数学公式手动计算。在实际应用中,根据数据的特性(如是否包含零或负数)和分析目的,选择合适的度量方法是很重要的。例如,几何平均值常用于计算不同时间段的增长率的平均值,而调和平均值常用于处理倒数型数据,如速率或密度的平均。
# 两个常用的统计包
import scipy.stats as stats
import numpy as np
# 我们拿两个数据集来举例
x1 = [1, 2, 2, 3, 4, 5, 5, 7]
x2 = x1 + [100]
2.1 平均值
np.mean(x1)
output
3.625
np.mean(x2)
output
14.333333333333334
print('x1的平均值:', sum(x1), '/', len(x1), '=', np.mean(x1))
print('x2的平均值:', sum(x2), '/', len(x2), '=', np.mean(x2))
output
x1的平均值: 29 / 8 = 3.625
x2的平均值: 129 / 9 = 14.333333333333334
2.2 中位数
print('x1的中位数:', np.median(x1))
print('x2的中位数:', np.median(x2))
output
x1的中位数: 3.5
x2的中位数: 4.0
2.3 众数
Scipy 具有内置的求众数功能,但它只返回-个值,即使两个值出现的次数相同,也只返回一个值。
print('x1的众数:', stats.mode(x1))
output
x1的众数: ModeResult(mode=2, count=2)
试一试
自定义求众数函数
def mode(x):
# 统计列表中每个元素出现的次数
counts = {}
for e in x:
if e in counts:
counts[e] += 1
else:
counts[e] = 1
# 返回出现次数最多的元素
maxcount = 0
modes = {}
for (key, value) in counts.items():
if value > maxcount:
maxcount = value
modes = {key}
elif value == maxcount:
modes.add(key)
if maxcount > 1 or len(x) == 1:
return list(modes)
return 'No mode'
print('x1的众数:', mode(x1))
output
x1的众数: [2, 5]
对于收益率数据可能没有哪个数据点会出现超过一次,此时应怎么处理?
可以使用bin值,正如我们构建直方图一样,此时统计哪个bin中数据点出现的次数多即可
import scipy.stats as stats
import numpy as np
import pandas as pd
# 获取收益率数据并计算出mode
# start = '2024-01-01'
# end = '2024-05-01'
s_601318 = pd.read_csv('./data/ch11_1.csv')
s_601318.head()
output
| ts_code | trade_date | open | high | low | close | pre_close | change | pct_chg | vol | amount | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 601318.SH | 20230331 | 45.60 | 46.30 | 45.38 | 45.60 | 45.48 | 0.12 | 0.2639 | 524539.93 | 2401305.125 |
| 1 | 601318.SH | 20230330 | 45.51 | 45.70 | 44.94 | 45.48 | 45.42 | 0.06 | 0.1321 | 450030.47 | 2035988.419 |
| 2 | 601318.SH | 20230329 | 46.33 | 46.58 | 45.40 | 45.42 | 45.88 | -0.46 | -1.0026 | 409020.05 | 1872693.109 |
| 3 | 601318.SH | 20230328 | 46.09 | 46.38 | 45.68 | 45.88 | 45.99 | -0.11 | -0.2392 | 283324.34 | 1300822.902 |
| 4 | 601318.SH | 20230327 | 46.26 | 46.33 | 45.50 | 45.99 | 46.20 | -0.21 | -0.4545 | 362172.67 | 1658727.910 |
s_601318.tail()
output
| ts_code | trade_date | open | high | low | close | pre_close | change | pct_chg | vol | amount | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2001 | 601318.SH | 20150109 | 71.20 | 78.18 | 70.72 | 72.84 | 71.08 | 1.76 | 2.48 | 3118734.02 | 2.316418e+07 |
| 2002 | 601318.SH | 20150108 | 74.50 | 74.92 | 70.80 | 71.08 | 73.41 | -2.33 | -3.17 | 1788809.15 | 1.288382e+07 |
| 2003 | 601318.SH | 20150107 | 73.30 | 75.50 | 72.50 | 73.41 | 73.73 | -0.32 | -0.43 | 1703868.84 | 1.256595e+07 |
| 2004 | 601318.SH | 20150106 | 74.38 | 76.77 | 72.01 | 73.73 | 76.16 | -2.43 | -3.19 | 2342279.69 | 1.743863e+07 |
| 2005 | 601318.SH | 20150105 | 77.80 | 78.80 | 75.25 | 76.16 | 74.71 | 1.45 | 1.94 | 2435717.73 | 1.875204e+07 |
returns = s_601318[['pct_chg']]
print('收益率众数:', stats.mode(returns))
# 由于所有的收益率都是不同的,所以我们使用频率分布来变相计算mode
hist, bins = np.histogram(returns, 20) # 将数据分成20个bin
maxfreq = max(hist)
# 找出哪个bin里面出现的数据点次数最大,这个bin就当做计算出来的mode
print('bins的众数:', [(bins[i], bins[i+1]) for i, j in enumerate(hist) if j == maxfreq])
output
收益率众数: ModeResult(mode=array([0.]), count=array([18.]))
bins的众数: [(-0.9910000000000014, 0.00999999999999801)]
2.4 几何平均值
使用Scipy包中的gmean函数来计算几何平均值
print('x1几何平均值:', stats.gmean(x1))
print('x2几何平均值:', stats.gmean(x2))
output
x1几何平均值: 3.0941040249774403
x2几何平均值: 4.552534587620071
计算几何平均值时出现负的观测值怎么办?
import scipy.stats as stats
import numpy as np
import pandas as pd
returns = s_601318['pct_chg']
# 计算几何平均值
ratios = returns + np.ones(len(returns)) # 在每个元素上增加1
r_g = stats.gmean(ratios) - 1 # 收益率的几何平均值
print('收益率的几何平均值:', r_g)
pricing = s_601318['close']
T = len(pricing)
init_price = pricing.iloc[0] # 获取初始价格
final_price = pricing.iloc[-1] # 获取最终价格
print('最初价格:', init_price)
print('最终价格:', final_price)
# 通过几何平均收益率计算的最终价格
estimated_final_price = init_price * (1 + r_g) ** T
print('通过几何平均收益率计算的最终价格:', estimated_final_price)
output
收益率的几何平均值: nan
最初价格: 45.6
最终价格: 76.16
通过几何平均收益率计算的最终价格: nan
D:\Program Files (x86)\anaconda3\lib\site-packages\scipy\stats_stats_py.py:197: RuntimeWarning: invalid value encountered in log
log_a = np.log(a)
# 在每个元素上增加1来计算几何平均值
import scipy.stats as stats
import numpy as np
# returns = s_601318['pct_chg'].dropna()
ratios = returns + 1
r_g = stats.gmean(ratios) - 1
print('收益率的几何平均值:', r_g)
pricing = s_601318['close']
T = len(pricing)
print(pricing[T-1])
init_price = pricing[0]
final_price = pricing[T-1]
print('最初价格:', init_price)
print('最终价格:', final_price)
print('通过几何平均收益率计算的最终价格:', init_price*(1 + r_g)**T)
output
收益率的几何平均值: nan
76.16
最初价格: 45.6
最终价格: 76.16
通过几何平均收益率计算的最终价格: nan
count_non_positive = (returns <= 0).sum()
if count_non_positive > 0:
print(f"共有{len(returns)}个样本数据,其中 {count_non_positive} 个小于等于0的数。")
else:
print("没有小于等于0的数。")
output
共有2006个样本数据,其中 1027 个小于等于0的数。
2.5 调和平均值
print('x1的调和平均值:', stats.hmean(x1))
print('x2的调和平均值:', stats.hmean(x2))
output
x1的调和平均值: 2.5590251332825593
x2的调和平均值: 2.869723656240511
3. 数据离散趋势的度量
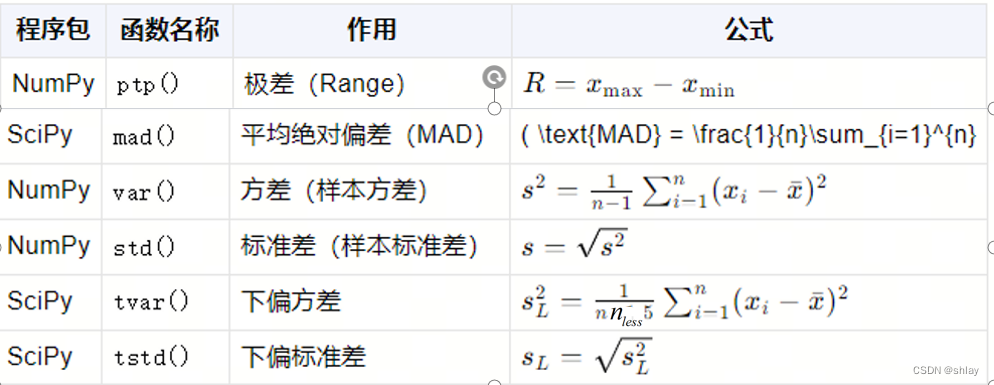
离散趋势的度量包括方差、标准差和极差等,它们衡量数据的变异程度。
- 使用场景: 了解数据的波动大小。
- 功能: 计算方差、标准差。
import numpy as np
np.random.seed(121)
# 生成20个小于100的随机整数
x3 = np.random.randint(100, size=20)
x3 = np.sort(x3)
print('x3: %s' %(x3))
mu = np.mean(x3)
print('x3的平均值:', mu)
output
x3: [ 3 8 34 39 46 52 52 52 54 57 60 65 66 75 83 85 88 94 95 96]
x3的平均值: 60.2
3.1 极差
np.max(x3)-np.min(x3)
output
93
print('x3的极差: %s' %(np.ptp(x3)))
output
x3的极差: 93
3.2 平均绝对偏差(MAD)
abs_dispersion = [np.abs(mu - x) for x in x3]
MAD = np.sum(abs_dispersion)/len(abs_dispersion)
print('x3的平均绝对偏差:', MAD)
output
x3的平均绝对偏差: 20.520000000000003
3.3 方差和标准差
print('x3的方差:', np.var(x3))
print('x3的标准差:', np.std(x3))
output
x3的方差: 670.16
x3的标准差: 25.887448696231154
3.4 下偏方差和下偏标准差
# 没有现成的计算下偏方差的函数,因此我们手动计算:
lows = [x for x in x3 if x <= mu]
semivar = np.sum( (lows - mu) ** 2 ) / len(lows)
print('x3的下偏方差:', semivar)
print('x3的下偏标准差:', np.sqrt(semivar))
output
x3的下偏方差: 689.5127272727273
x3的下偏标准差: 26.258574357202395
3.5 目标下偏方差和目标下偏标准差
goal_num = 19 # 目标为19
lows_g = [x for x in x3 if x <= goal_num]
semivar_g = sum(list(map(lambda x: (x - goal_num)**2,lows_g)))/len(lows_g)
print('x3的目标下偏方差:', semivar_g)
print('x3的目标下偏标准差:', np.sqrt(semivar_g))
output
x3的目标下偏方差: 188.5
x3的目标下偏标准差: 13.729530217745982
4. 峰度、偏度与正态性检验
峰度和偏度是衡量数据分布形态的统计量,正态性检验用于判断数据是否近似正态分布。
- 使用场景: 分析数据分布的形状。
- 功能: 计算峰度、偏度,进行正态性检验。
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
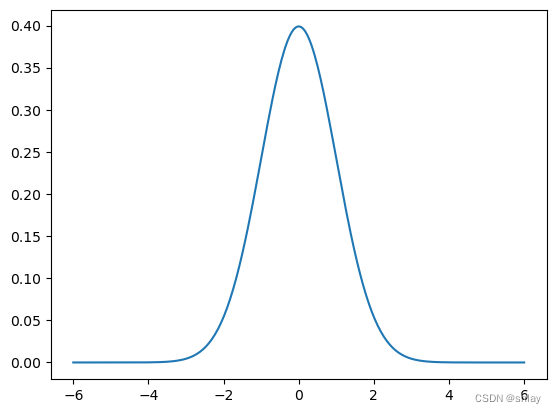
xs = np.linspace(-6,6, 300)
normal = stats.norm.pdf(xs)
plt.plot(xs, normal);
# 产生数据
xs2 = np.linspace(stats.lognorm.ppf(0.01, .7, loc=-.1), stats.lognorm.ppf(0.99, .7, loc=-.1), 150)
4.1 偏度
偏度(Skewness)是统计学中描述数据分布不对称性的度量。它告诉我们数据分布的尾部是长于左侧还是右侧,或者说分布是偏向左侧还是右侧。偏度的特点可以通过以下几个方面来介绍:
-
- 定义:偏度是三阶标准化矩,它衡量了数据分布的偏斜程度。
-
- 计算公式:偏度通常用第三阶标准化矩来计算,公式为:
Skewness = n ( n − 1 ) ( n − 2 ) ∑ ( X i − X ˉ s ) 3 \text{Skewness} = \frac{n}{(n-1)(n-2)} \sum \left(\frac{X_i - \bar{X}}{s}\right)^3 Skewness=(n−1)(n−2)n∑(sXi−Xˉ)3
其中, X i X_i Xi 是样本数据点, X ˉ \bar{X} Xˉ 是样本均值, s s s 是样本标准差, n n n 是样本大小。
-
- 取值范围:偏度的取值可以是任意实数。它不受正负限制。
-
- 解释:
- 正偏度(右偏态):如果偏度值大于0,数据分布呈现正偏度,意味着数据的尾部向右延伸,数据的分布形态是不对称的,有一个长的右尾和短的左尾。在这种情况下,均值大于中位数。
- 负偏度(左偏态):如果偏度值小于0,数据分布呈现负偏度,意味着数据的尾部向左延伸,同样数据分布是不对称的,有一个长的左尾和短的右尾。在这种情况下,均值小于中位数。
- 零偏度:如果偏度值接近0,数据分布接近对称,但并不一定是完美的对称分布。
-
- 使用场景:偏度是数据分析中的一个重要工具,特别是在探索性数据分析阶段。它可以帮助识别数据分布的特性,对于正态性检验、异常值检测、风险评估和投资回报分析等领域都有应用。
-
- 局限性:偏度对异常值敏感,异常值可能会对偏度的计算结果产生较大影响。此外,偏度不能告诉我们分布的具体形态,只能提供关于分布不对称性的定性信息。
# 偏度>0
lognormal = stats.lognorm.pdf(xs2, .7)
plt.plot(xs2, lognormal, label='Skew > 0')
# 偏度<0
plt.plot(xs2, lognormal[::-1], label='Skew < 0')
plt.legend()

4.2 峰度
峰度(Kurtosis)是统计学中描述数据分布形态的另一个重要统计量,它衡量数据分布的“尖峭”或“平坦”程度,也就是分布的尾部相对重量的度量。以下是峰度的一些特点:
-
- 定义:峰度是四阶标准化矩,它描述了数据分布的尾部相对于正态分布的尾部的相对大小。
-
- 计算公式:峰度通常用第四阶标准化矩来计算,公式为:
Kurtosis = n ( n + 1 ) ( n − 1 ) ( n − 2 ) ( n − 3 ) ∑ ( X i − X ˉ s ) 4 − 3 ( n − 1 ) 2 ( n − 2 ) ( n − 3 ) \text{Kurtosis} = \frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum \left(\frac{X_i - \bar{X}}{s}\right)^4 - \frac{3(n-1)^2}{(n-2)(n-3)} Kurtosis=(n−1)(n−2)(n−3)n(n+1)∑(sXi−Xˉ)4−(n−2)(n−3)3(n−1)2
其中, X i X_i Xi 是样本数据点, X ˉ \bar{X} Xˉ 是样本均值, s s s 是样本标准差, n n n 是样本大小。
- 计算公式:峰度通常用第四阶标准化矩来计算,公式为:
-
- 取值范围:峰度的取值可以是任意实数。
-
- 解释:
- 正峰度(Leptokurtic):如果峰度值大于0,数据分布比正态分布更尖锐,有更明显的峰,尾部相对较轻。这表明数据中有极端值的可能性更高。
- 零峰度:如果峰度值接近0,数据分布的形状与正态分布相似,有时称为“ mesokurtic”,即中等峰度。
- 负峰度(Platykurtic):如果峰度值小于0,数据分布比正态分布更平坦,峰宽更宽,尾部相对较重。这表明数据中的极端值较少。
-
- 使用场景:峰度可以用于风险管理、金融投资分析、信号处理等领域,帮助了解数据分布的特性。
-
- 局限性:峰度也对异常值敏感,异常值可能会对峰度的计算结果产生较大影响。
请注意,不同统计软件和书籍可能会采用不同的峰度定义,有些会从计算结果中减去3,以便于比较正态分布的峰度为0。在使用时,需要确认所使用的库或函数的具体实现方式。
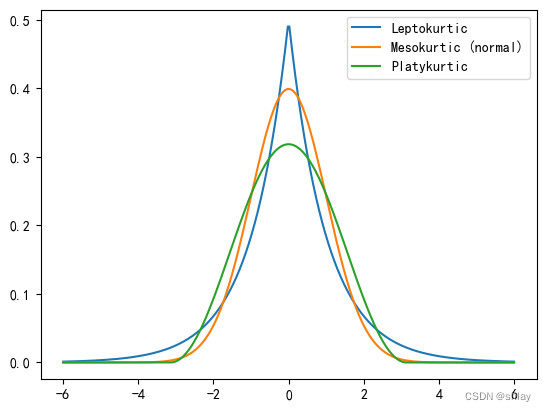
plt.plot(xs,stats.laplace.pdf(xs), label='Leptokurtic')
print('尖峰的超额峰度:', (stats.laplace.stats(moments='k')))
plt.plot(xs, normal, label='Mesokurtic (normal)')
print('正态分布超额峰度:', (stats.norm.stats(moments='k')))
plt.plot(xs,stats.cosine.pdf(xs), label='Platykurtic')
print('平峰超额峰度:', (stats.cosine.stats(moments='k')))
plt.legend()
output
尖峰的超额峰度: 3.0
正态分布超额峰度: 0.0
平峰超额峰度: -0.5937628755982794
4.3 正态性检验
4.3.1 Jarque-Bera(大样本)
Jarque-Bera (JB) 检验是一种用于检测数据是否服从正态分布的统计方法。它基于数据的偏度和峰度,检验数据分布的对称性和尖峭程度是否与正态分布一致。JB检验的基本原理如下:
-
- 偏度和峰度:JB检验利用了偏度(Skewness)和峰度(Kurtosis)两个统计量。偏度衡量分布的对称性,而峰度衡量分布的尖峭程度。
-
- 正态分布的假设:在正态分布的假设下,偏度应该接近0,表示分布是对称的;峰度应该接近3,因为正态分布的峰度是3。
-
- 检验统计量:JB检验的统计量是基于偏度的平方和峰度与3的差的平方,通过以下公式计算:
J B = n ⋅ [ ( S 6 ) 2 + ( K − 3 ) 2 24 ] JB = n \cdot \left[\left(\frac{S}{\sqrt{6}}\right)^2 + \frac{(K - 3)^2}{24}\right] JB=n⋅[(6S)2+24(K−3)2]
其中, S S S 是样本偏度, K K K 是样本峰度, n n n 是样本大小。
- 检验统计量:JB检验的统计量是基于偏度的平方和峰度与3的差的平方,通过以下公式计算:
-
- 卡方分布:计算得到的JB统计量遵循自由度为2的卡方分布 χ 2 2 \chi^2_2 χ22。
-
- p值:通过比较JB统计量与卡方分布的临界值,可以得到p值。如果p值小于给定的显著性水平(例如0.05),则拒绝正态分布的假设。
-
- 使用场景:JB检验常用于金融数据分析、社会科学、经济研究等领域,尤其是在数据集较大时更为可靠。
-
- 局限性:对于小样本数据,JB检验的功效(检测非正态分布的能力)可能不足。此外,如果数据中包含极端值或异常值,JB检验的结果可能会受到响。
from statsmodels.stats.stattools import jarque_bera
_, pvalue, _, _ = jarque_bera(xs)
if pvalue > 0.05:
print('xs数据服从正态分布.')
else:
print('xs数据并不服从正态分布.')
output
xs数据并不服从正态分布.
from statsmodels.stats.stattools import jarque_bera
data = np.random.normal(0, 1, 1000) # 假设有一个正态分布的样本数据
_, pvalue, _ ,_= jarque_bera(data)
if pvalue > 0.05:
print('数据服从正态分布.')
else:
print('数据并不服从正态分布.')
output
数据服从正态分布.
4.3.2 $ D’Agostino’s K^2$ 检验(中小样本)
简介:$ D’Agostino’s K^2 检验也是一种基于偏度和峰度的检验方法,它是由 D ′ A g o s t i n o 、 B e l a n g e r 和 D ′ A g o s t i n o J r . 提出的,用于改进 K o l m o g o r o v − S m i r n o v 检验在正态性检验方面的性能 , 适用于中小样本。 检验也是一种基于偏度和峰度的检验方法,它是由D'Agostino、Belanger和D'Agostino Jr. 提出的,用于改进Kolmogorov-Smirnov检验在正态性检验方面的性能,适用于中小样本。 检验也是一种基于偏度和峰度的检验方法,它是由D′Agostino、Belanger和D′AgostinoJr.提出的,用于改进Kolmogorov−Smirnov检验在正态性检验方面的性能,适用于中小样本。 D’Agostino’s K^2$检验的基本原理如下:
-
- 基于偏度和峰度:$ D’Agostino’s K^2$ 检验同时考虑了数据分布的偏度(Skewness)和峰度(Kurtosis)。这两个统计量分别描述了数据分布的对称性和尖峭程度。
-
- 正态分布的假设:在正态分布的假设下,偏度接近0,表示分布是对称的;峰度接近3,因为正态分布的峰度是3。
-
- 检验统计量:$ D’Agostino’s K^2$检验的统计量是通过将样本偏度的平方和样本峰度与3的差的平方结合起来计算的,公式为:
K 2 = ( n − 1 ) S 2 ( n − 2 ) + ( n − 2 ) ( K + 3 ) 2 n K^2 = \frac{(n-1)S^2}{(n-2)} + \frac{(n-2)(K+3)^2}{n} K2=(n−2)(n−1)S2+n(n−2)(K+3)2
其中, S S S 是样本偏度, K K K 是样本峰度, n n n 是样本大小。
- 检验统计量:$ D’Agostino’s K^2$检验的统计量是通过将样本偏度的平方和样本峰度与3的差的平方结合起来计算的,公式为:
-
- 卡方分布:计算得到的K^2统计量可以与卡方分布进行比较,以确定其显著性。
-
- p值:通过比较 K 2 K^2 K2统计量与卡方分布的临界值,可以得到p值。如果p值小于给定的显著性水平(例如0.05),则拒绝正态分布的假设。
-
- 适用性:$ D’Agostino’s K^2$ 检验适用于样本大小在4到5000之间的数据集。对于非常小的样本或非常大的样本,该检验的功效可能会受到影响。
-
- 局限性:$ D’Agostino’s K^2$检验对异常值敏感,数据中的异常值可能会对检验结果产生较大影响。
在Python中,可以使用 scipy.stats 中的 normaltest 函数来执行$ D’Agostino’s K^2$ 检验:
from scipy.stats import normaltest
data = np.random.normal(0, 1, 100) # 假设有一个正态分布的样本数据
k2_statistic, pvalue = normaltest(data)
print(f"D'Agostino's K^2\n 统计量: {k2_statistic},\n p 值: {pvalue}")
if pvalue > 0.05:
print('数据服从正态分布.')
else:
print('数据并不服从正态分布.')
output
D’Agostino’s K^2
统计量: 4.065424312057413,
p 值: 0.13097980132490886
数据服从正态分布.
4.3.3 Shapiro-Wilk 检验(小样本)
简介:Shapiro-Wilk检验是一种基于数据排序和平均值差异的用于小样本数据的正态性检验方法,它是由Roy P. Shapiro和Martin Wilk在1965年提出的。这种检验特别适用于样本量小于50的情况。Shapiro-Wilk检验的基本原理如下:
-
- 线性组合:Shapiro-Wilk检验通过计算样本数据的线性组合,这个线性组合是基于样本数据与其正态分布理论值的偏差。
-
- 标准化:检验中使用的样本数据是经过标准化处理的,以消除量纲和样本大小的影响。
-
- 检验统计量:Shapiro-Wilk检验的统计量
W
W
W 是通过以下公式计算的:
W = R n − 1 / R n W = R_{n-1} / R_n W=Rn−1/Rn
其中, R i R_i Ri 是样本数据的第 i i i 个有序值与其正态分布理论中值的差的绝对值之和。
- 检验统计量:Shapiro-Wilk检验的统计量
W
W
W 是通过以下公式计算的:
-
- 分布: W W W 统计量的值与正态分布的理论值进行比较。如果 W W W 的值偏离1太多,那么可以认为样本数据不是正态分布的。
-
- p值:计算得到的 W W W 统计量与正态分布的理论值进行比较,得到p值。如果p值小于给定的显著性水平(例如0.05),则拒绝正态分布的假设。
-
- 适用性:Shapiro-Wilk检验适用于小样本数据,通常样本量小于50。对于较大的样本,其检验功效可能不如其他检验方法,如Kolmogorov-Smirnov检验。
-
- 局限性:Shapiro-Wilk检验对异常值敏感,样本中的异常值可能会对检验结果产生较大影响。
在Python中,可以使用 scipy.stats 中的 shapiro 函数来进行Shapiro-Wilk检验:
from scipy.stats import shapiro
data = np.random.normal(0, 1, 20) # 假设有一个正态分布的样本数据
shapiro_statistic, pvalue = shapiro(data)
print(f"Shapiro-Wilk\n 统计量: {shapiro_statistic},\n p 值: {pvalue}")
if pvalue > 0.05:
print('数据服从正态分布.')
else:
print('数据并不服从正态分布.')
output
Shapiro-Wilk
统计量: 0.8549917936325073,
p 值: 0.006469838321208954
数据并不服从正态分布.
4.3.4 Kolmogorov-Smirnov (K-S) 检验
简介:K-S检验是一种非参数检验,用于比较数据分布(累积分布函数,CDF)和理论分布(在正态性检验的情况下,通常是正态分布)之间的差异。以下是K-S检验的基本原理:
-
- 累积分布函数:K-S检验比较了样本数据的累积分布函数与理论分布(正态分布)的累积分布函数之间的最大差异。
-
- 最大绝对偏差:检验统计量是样本CDF与理论CDF之间的最大绝对偏差,表示为:
D n = sup x ∣ F n ( x ) − F ( x ) ∣ D_n = \sup_x |F_n(x) - F(x)| Dn=xsup∣Fn(x)−F(x)∣
其中, F n ( x ) F_n(x) Fn(x) 是样本数据的经验CDF, F ( x ) F(x) F(x) 是理论CDF(在正态性检验中为正态分布的CDF)。
- 最大绝对偏差:检验统计量是样本CDF与理论CDF之间的最大绝对偏差,表示为:
-
- 正态性检验:在正态性检验中,K-S检验用于确定样本数据是否与正态分布有显著差异。
-
- 检验统计量:K-S检验的统计量是标准化的最大偏差,对于样本大小为
n
n
n 的样本,计算公式为:
K S = n D n KS = \sqrt{n} D_n KS=nDn
- 检验统计量:K-S检验的统计量是标准化的最大偏差,对于样本大小为
n
n
n 的样本,计算公式为:
-
- 分布:K-S统计量 D n D_n Dn 的确切分布可以通过模拟得到,或者对于大样本,可以使用极限分布,即Kolmogorov分布。
-
- p值:通过比较计算得到的 D n D_n Dn 统计量与正态分布下的临界值,可以得到p值。如果p值小于给定的显著性水平(例如0.05),则拒绝正态分布的假设。
-
- 适用性:K-S检验适用于大样本数据,尤其是当样本量较大时,它是一种非常强大的检验方法。
-
- 局限性:对于小样本数据,K-S检验的功效可能不足。此外,K-S检验对于数据中的异常值不敏感,这可能是优点也可能是缺点,取决于数据的特性。
在Python中,可以使用 scipy.stats 中的 kstest 函数来进行K-S检验:
from scipy.stats import kstest
data = np.random.normal(0, 1, 100) # 假设有一个正态分布的样本数据
ks_statistic, pvalue = kstest(data, 'norm')
print(f"Kolmogorov-Smirnov:\n 统计量: {ks_statistic},\n p 值: {pvalue}")
if pvalue > 0.05:
print('数据服从正态分布.')
else:
print('数据并不服从正态分布.')
output
Kolmogorov-Smirnov:
统计量: 0.05132494131397103,
p 值: 0.942571302915555
数据服从正态分布.
4.3.5 Anderson-Darling 检验
简介:Anderson-Darling检验是一种衡量样本数据与正态分布差异的检验方法,适用于各种样本大小。
Anderson-Darling 检验是一种用于评估数据是否来自某个特定分布(如正态分布)的统计方法。这种检验特别适用于小样本数据,并且可以用来检验样本数据是否服从正态分布。以下是Anderson-Darling检验的基本原理:
-
- 基于顺序统计量:Anderson-Darling检验基于样本数据的顺序统计量。它比较了数据的有序统计量与正态分布的理论累积分布函数(CDF)。
-
- 检验统计量:检验统计量是通过计算样本数据与正态分布的理论值之间的偏差来得到的。具体来说,它是样本数据与正态分布的理论中位数之间差异的度量。
-
- A^2 统计量:Anderson-Darling检验的统计量通常表示为
A
2
A^2
A2,计算公式为:
A 2 = − n − 1 n ∑ i = 1 n ( 2 i − 1 n − P ( X i ) ) 2 log P ( X i ) A^2 = -n - \frac{1}{n} \sum_{i=1}^{n} \left( \frac{2i-1}{n} - P(X_i) \right)^2 \log P(X_i) A2=−n−n1i=1∑n(n2i−1−P(Xi))2logP(Xi)
其中, X i X_i Xi 是样本数据的有序统计量, P ( X i ) P(X_i) P(Xi) 是正态分布的累积分布函数对于有序统计量 X i X_i Xi的值, n n n 是样本大小。
- A^2 统计量:Anderson-Darling检验的统计量通常表示为
A
2
A^2
A2,计算公式为:
-
- 分布: A 2 A^2 A2统计量在正态分布下的确切分布是未知的,但可以通过模拟得到其分布表或使用近似方法。
-
- p值:通过比较计算得到的 A 2 A^2 A2统计量与正态分布下的临界值,可以得到p值。如果p值小于给定的显著性水平(例如0.05),则拒绝正态分布的假设。
-
- 适用性:Anderson-Darling检验适用于小样本数据,当样本量较小时,它比Kolmogorov-Smirnov检验更敏感。
-
- 局限性:虽然Anderson-Darling检验适用于小样本,但它不适用于大样本,因为大样本下 A 2 A^2 A2统计量的分布变得非常复杂。
在Python中,可以使用 scipy.stats 中的 anderson 函数来进行Anderson-Darling检验:
anderson 函数返回一个包含多个统计量和对应p值的元组,其中result.statistic是统计量,result.significance_level是p值。如果p值很小,那么我们有足够的证据拒绝正态性的假设,认为数据不是正态分布的。反之,如果p值较大,我们没有足够的证据拒绝正态性假设,数据可能近似正态分布。
from scipy.stats import anderson
data = np.random.normal(0, 1, 100) # 假设有一个正态分布的样本数据
result = anderson(data, 'norm')
print(f"Anderson-Darling \n统计量: {result.statistic}, \n p 值: {result.significance_level}")
if result.significance_level[0] > 0.05:
print('数据服从正态分布.')
else:
print('数据并不服从正态分布.')
output
Anderson-Darling
统计量: 0.2907712143572354,
p 值: [15. 10. 5. 2.5 1. ]
数据服从正态分布.
4.3.6 Q-Q图和P-P图
简介:Q-Q图和P-P图是两种常用的图示法进行正态性检验的工具,通过将样本数据与正态分布的理论值进行比较,来直观判断数据是否正态分布。
- 1、Q-Q图(Quantile-Quantile Plot)
Q-Q图的原理是比较样本数据的分位数与正态分布的理论分位数。如果数据服从正态分布,那么样本数据的分位数应该与正态分布的理论分位数大致一致,即在Q-Q图上,数据点应该大致沿着一条直线排列。
Q-Q图的检验步骤:
- 计算样本数据的分位数。
- 计算正态分布的理论分位数。
- 在图上绘制样本分位数(通常作为纵坐标)和理论分位数(横坐标)。
如果数据点紧密围绕着对角线分布,这表明数据服从正态分布。如果数据点显著偏离这条直线,则表明数据可能不服从正态分布。
- 2、P-P图(Probability-Probability Plot)
P-P图的原理是将样本数据的累积概率与正态分布的理论累积概率进行比较。与Q-P图类似,如果数据服从正态分布,那么样本的累积概率与理论累积概率应该大致对等,即在P-P图上,数据点也应该大致沿着一条直线排列。
P-P图的检验步骤:
- 计算样本数据的累积概率。
- 计算正态分布的理论累积概率。
- 在图上绘制样本的累积概率(通常作为纵坐标)和理论累积概率(横坐标)。
P-P图的结果通常包括正态P-P图和去趋势的正态P-P图。去趋势的P-P图可以帮助我们进一步考虑实测累积概率与预期累积概率间的差别,如果残差基本在Y=0上下均匀分布,说明数据的正态性较好。
Q-Q图和P-P图都是通过图形的方式直观地评估数据是否符合正态分布。两者的主要区别在于它们比较的是不同类型的概率(分位数 vs 累积概率)。在实际操作中,这两种图示法可以相互补充,提供更全面的正态性检验视角。
import matplotlib.pyplot as plt
from scipy.stats import probplot
data = np.random.normal(0, 1, 100) # 假设有一个正态分布的样本数据
probplot(data, dist="norm", plot=plt)
plt.show()
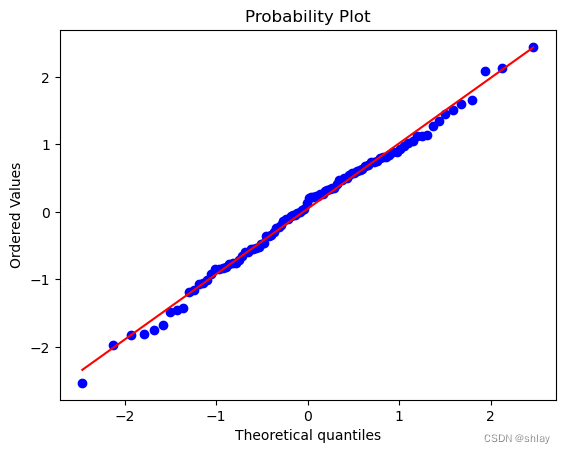
import matplotlib.pyplot as plt
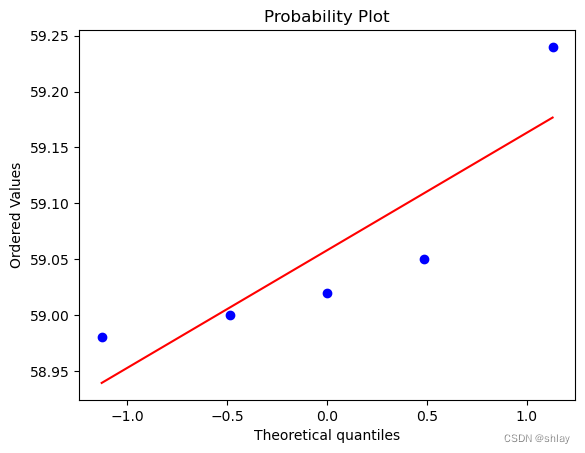
from scipy.stats import probplot
probplot(pricing, dist="norm", plot=plt)
plt.show()
5. 异常数据识别与处理
5.1 初始数据查看
数据文件“ch11_1.csv”下载
import scipy.stats as stats
import numpy as np
import pandas as pd
# 获取收益率数据并计算出mode
# start = '2024-01-01'
# end = '2024-05-01'
s_601318 = pd.read_csv('./data/ch11_1.csv')
print(s_601318.head())
returns = s_601318[['pct_chg']]
output
ts_code trade_date open high low close pre_close change
0 601318.SH 20230331 45.60 46.30 45.38 45.60 45.48 0.12
1 601318.SH 20230330 45.51 45.70 44.94 45.48 45.42 0.06
2 601318.SH 20230329 46.33 46.58 45.40 45.42 45.88 -0.46
3 601318.SH 20230328 46.09 46.38 45.68 45.88 45.99 -0.11
4 601318.SH 20230327 46.26 46.33 45.50 45.99 46.20 -0.21
pct_chg vol amount
0 0.2639 524539.93 2401305.125
1 0.1321 450030.47 2035988.419
2 -1.0026 409020.05 1872693.109
3 -0.2392 283324.34 1300822.902
4 -0.4545 362172.67 1658727.910
returns.describe()
output
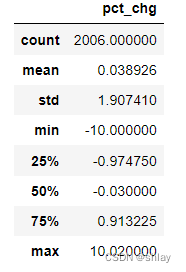
returns.hist(bins=100)
output
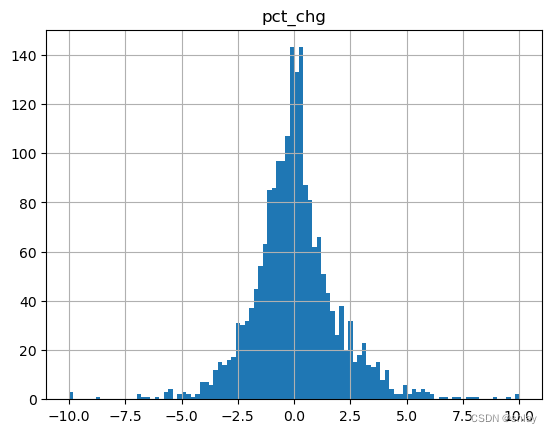
pricing = s_601318['close']
pricing.describe()
output
count 2006.000000
mean 59.178490
std 19.027541
min 25.110000
25% 42.582500
50% 59.145000
75% 76.615000
max 93.380000
Name: close, dtype: float64
pricing.hist(bins=30)
output
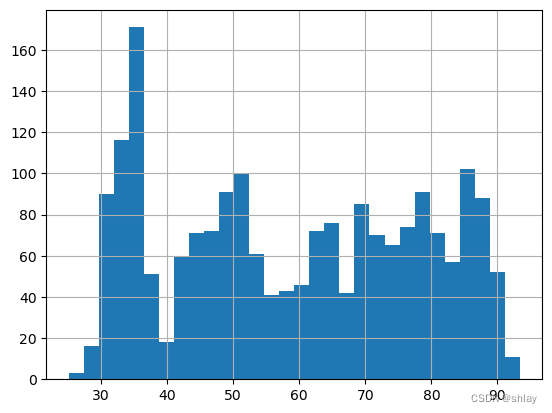
5.2 固定比例法
根据固定的比例剔除数据的上下限。
print('均值:',pricing.mean())
print('标准差:',pricing.std())
pricing.hist(bins=100)
output
均值: 59.17649700897307
标准差: 18.99295830716207
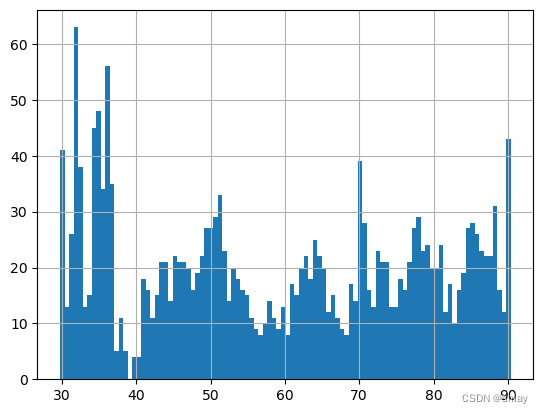
pricing[pricing >= pricing.quantile(0.99)] = pricing.quantile(0.99)
pricing[pricing <= pricing.quantile(0.01)] = pricing.quantile(0.01)
print('均值:',pricing.mean())
print('标准差:',pricing.std())
pricing.hist(bins=100)
output
均值: 59.1765268444666
标准差: 18.992880319153933
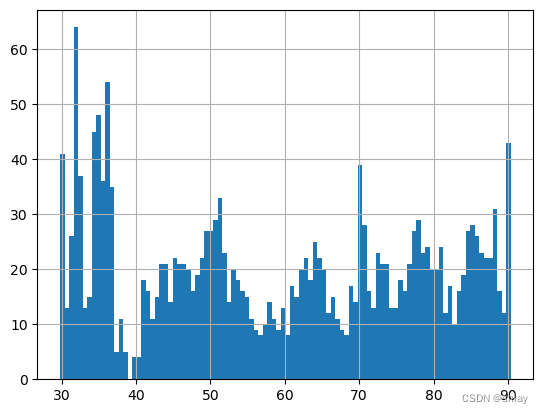
5.3 均值标准差法
利用均值和标准差定义的阈值来剔除异常值。
pricing[pricing >= pricing.mean() + 3*pricing.std()] = pricing.mean() + 3*pricing.std()
pricing[pricing <= pricing.mean() - 3*pricing.std()] = pricing.mean() - 3*pricing.std()
print('均值:',pricing.mean())
print('标准差:',pricing.std())
pricing.hist(bins=100)
output
均值: 59.1765268444666
标准差: 18.992880319153933
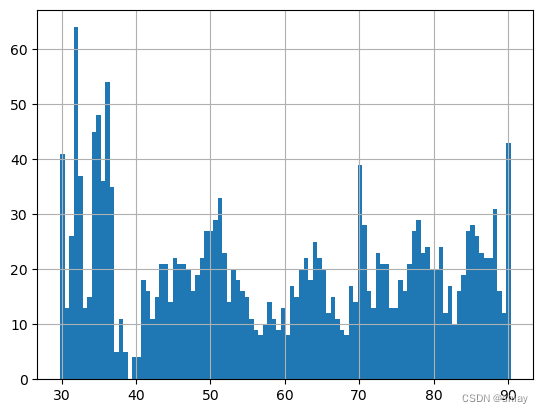
5.4 MAD法
使用中位数绝对偏差(MAD)来识别异常值。
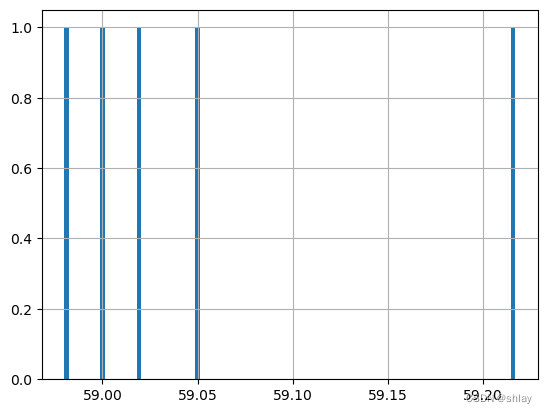
med = np.median(list(pricing))
MAD = np.mean(abs(pricing) - med)
pricing = pricing[abs(pricing-med)/MAD <=6] # 剔除偏离中位数6倍以上的数据
print('均值:',pricing.mean())
print('标准差:',pricing.std())
pricing.hist(bins=100)
output
均值: 59.05800000000001
标准差: 0.10497618777608689

5.5 Boxplot法
使用箱线图的方法识别异常值。
from statsmodels.stats.stattools import medcouple
pricing = pricing.dropna()
def boxplot(data):
#mc可以使用statsmodels包中的medcouple函数直接进行计算
mc = medcouple(data)
data.sort()
q1 = data[int(0.25 * len(data))]
q3 = data[int(0.75 * len(data))]
iqr = q3-q1
if mc >= 0:
l = q1-1.5 * np.exp(-3.5 * mc) * iqr
u = q3 + 1.5 * np.exp(4 * mc) * iqr
else:
l = q1 - 1.5 * np.exp(-4 * mc) * iqr
u = q3 + 1.5 * np.exp(3.5 * mc) * iqr
data = pd.Series(data)
data[data < l] = l
data[data > u] = u
return data
print('均值',boxplot(list(pricing)).mean())
print('标准差',boxplot(list(pricing)).std())
boxplot(list(pricing)).hist(bins=100)
output
均值 59.05338311392736
标准差 0.09500471052525994