1、向量的点积

数量积又称标量积（Scalar product）、点积（Dot product），在欧几里得空间（Euclidean space）中称为内积（Inner product），对应元素相乘相加，结果是一个标量（即一个数）。

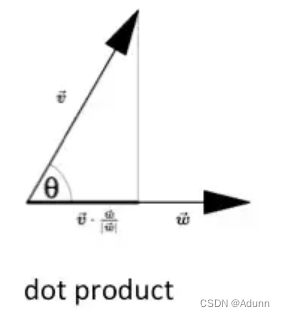
示例：

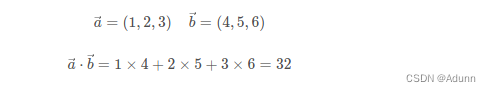
在numpy中 使用np.dot或numpy.inner()实现向量的点积

import numpy as np 
a = np.array([1,2,3])
b = np.array([4,5,6])

## 数量积  使用np.dot或np.inner
print(np.dot(a,b))

大家对点积比较熟悉，物理中功的定义就是力和位移的点积，功是个标量：

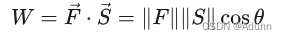
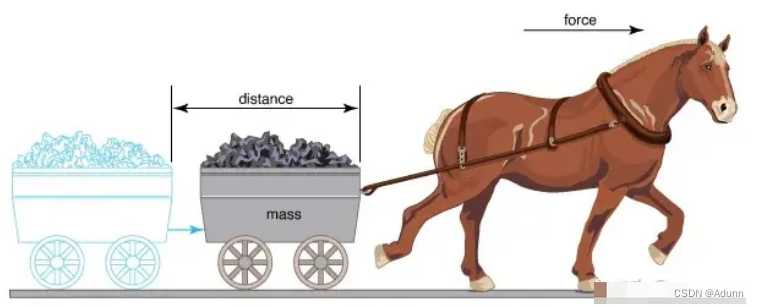
对于两个向量：

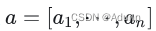
和

，点积

其中最后一个等号为爱因斯坦求和记号(Einstein summation notation)，用于简化sigma表达。

2、向量的叉积

叉积，也称向量积，又称矢量积（Vector product）、叉积（Cross product）、外积（Outer product），结果是一个向量。

叉积是两个向量在三维欧氏空间中的二元操作，但叉积仅限于三维空间，对于其他维度的空间，则要使用外积，因此，不严谨的，可将叉积视为外积在三维空间中的特殊情况(有点瑕疵)。

示例：

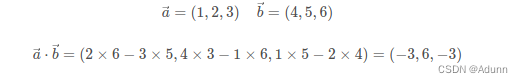
numpy中 使用np.cross实现向量的叉积

import numpy as np 

a = np.array([1,2,3])
b = np.array([4,5,6])

## 叉积  使用np.cross
print(np.cross(a,b))

对于两个向量
其中：
分别表示两个向量的模长，
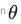表示两个向量在其构建的平面中的夹角，

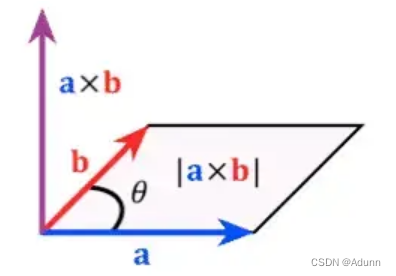
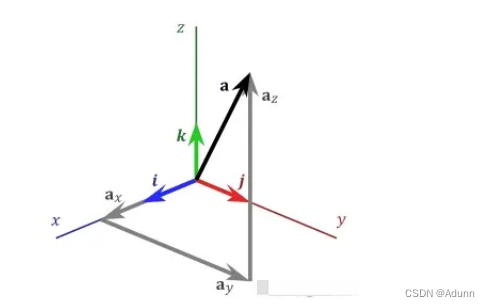
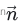是单位向量，垂直于这两个向量所张成的平面，方向可用下图的右手定则确定。

显然，叉积不满足交换律，而满足反交换律：

，即向量交换后，结果向量方向相反，不信伸出您的右手，比划下：

当两个向量平行时，两者夹角为0度，sine等于0，叉积也为0，几何上，共线的两个向量无法张成一个平行四边形；线性代数的角度，这两个向量线性相关了，无法张成(span)平面。显然，任何向量自叉乘为0：

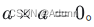
当两个向量垂直时，它们夹角为90度，sine为1，叉乘达到最大值 ：

3、矩阵的点积

对于A 矩阵（m × s 阶），B 矩阵（s × n阶）（A的列数与B的行数相等），

两者的点积，即矩阵相乘的结果C = A B 是m × n 阶矩阵，

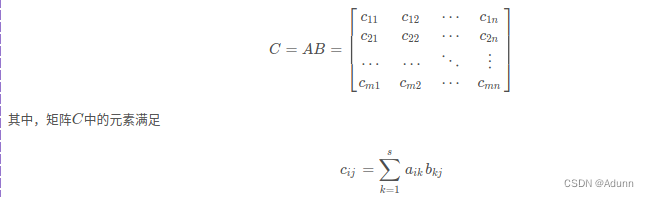
示例：

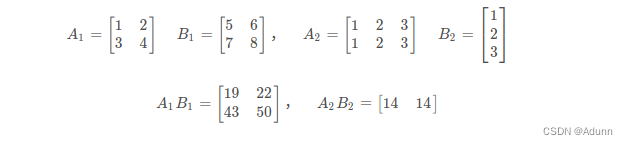
numpy实现

import numpy as np 

A1 = np.array([[1,2],[3,4]])
B1 = np.array([[5,6],[7,8]])
A2 = np.array([[1,2,3],[1,2,3]])
B2 = np.array([1,2,3])

## 数量积  使用np.dot
print(np.dot(A1,B1))
print(np.dot(A2,B2))

此外，numpyt提供了numpy.inner()函数，从字面意思理解是内积，其针对向量numpy.inner()与numpy.dot()输出一致，但针对矩阵有所不同。

print(np.inner(A1,B1))

print(np.inner(A2,B2))

4、矩阵的叉积

针对矩阵并不存在叉积的概念，numpy中针对矩阵的叉积运算是按照向量的叉积进行运算。

示例：

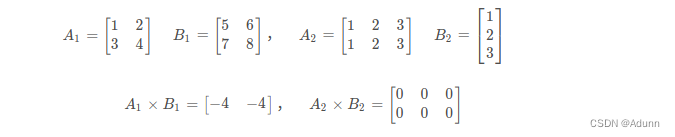
numpy实现

import numpy as np 

A1 = np.array([[1,2],[3,4]])
B1 = np.array([[5,6],[7,8]])
A2 = np.array([[1,2,3],[1,2,3]])
B2 = np.array([1,2,3])

## 叉积  使用np.cross
print(np.cross(A1,B1))
print(np.cross(A2,B2))