树(Tree)

"树"这种数据很像现实生活中的“树”, 这里的每个元素我们叫做“节点”
用来连线相邻节点之间的关系,我们叫做“父子关系”
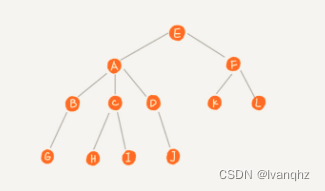
- A节点就是B节点的父节点,B节点是A节点的‘子节点’
- B,C,D这三个节点的父节点是同一个节点,所以它们是
兄弟节点 - 把没有父节点的节点叫做
根节点,也图中的E - 把没有子节点的节点叫做
叶子节点或者叶节点,比如图中的G,H, I, J, K, L
高度(Height),深度(Depth),层(Level)
概述
节点的高度:节点到叶子节点的最长路径(边数)
节点的深度:根节点到这个节点所经历的边的个数
- 节点的层数:节点的深度 + 1
- 树的高度: 根节点的高度
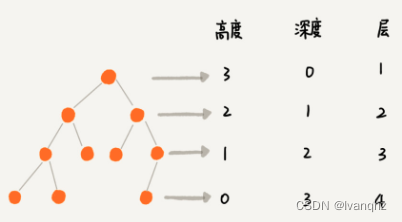
高度
- 其实就是从下往上度量,比如我们要度量第10层楼的高度,第13层楼的高度,起点都是地面
- 所以,树这种数据结构的高度也是一样,从最底层开始计数,并且计数的起点都是0
深度
- 从上往下度量。比如水中与的深度,是从水平面开始度量
- 所有,树这种数据结构的深度也是类似的,从根节点开始度量,并且计数起点也是0
层数
- 与深度类似,不过,计数起点是1,也就是根节点的位于第1层
二叉树(Binary Tree)
概述
每个节点最多有两个“叉”,也就是两个子节点,分别是左子节点和右子节点

满二叉树
图中编号2的二叉树。叶子节点全都在最底层
除了叶子节点之外,每个节点都有左右两个子节点,这种二叉树叫做满二叉树
完全二叉树
编号3的二叉树,叶子节点都在最底下两层,最后一层的叶子节点都靠左
并且除了最后一层,其他层的节点个数都要达到最大,这种二叉树叫做完全二叉树
二叉树存储方式
链表存储法
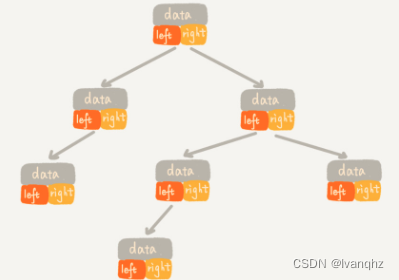
每个节点都有三个字段,其中一个存储数据,另外两个是指向左右子节点指针
我们只要拎住根节点,就可以通过左右子节点的指针,把整棵树都串起来
大部分二叉树代码都是通过这种结构实现的
顺序存储法
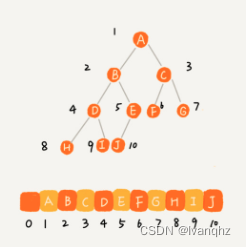
把根节点存储在下标i = 1的位置,那左子节点存储在下标 2 * i = 2 的位置,右子节点存储在 2 * i + 1 = 3 的位置
以此类推,B节点的左子节点存储在 2 * i = 2 * 2 = 4的位置,右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5的位置
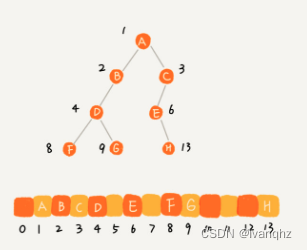
为什么偏偏把最后一层的叶子节点靠左排列的叫做完全二叉树?
- 从上图看出,一颗完全二叉树,仅仅“浪费”了一个下标为0的存储位置,如果非完全二叉树,则会浪费比较多的数组存储空间
二叉树遍历
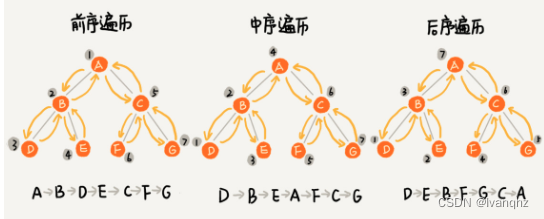
前序遍历
对于树中任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的左子树
中序遍历
对于树中任意节点来说,先打印它的左子树,然后再打印它本省,最后打印它的右子树
后序遍历
对于树中任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身
时间复杂度
从上图可以看出,每个节点最多会被访问两次,所以遍历操作的时间复杂度,跟节点的个数n成正比,也就是时间复杂度: O(n)
代码展示

参考资料
- 卡特兰数 — 计数的映射方法的伟大胜利



![[C++] 从零实现一个ping服务](https://img-blog.csdnimg.cn/img_convert/7b0d6ba5dcce6ce6b2e732fdffde6496.gif#pic_center)