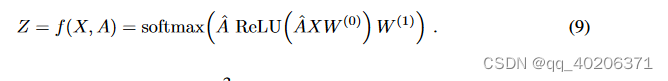ICLR 2017

1 abstract和intro部分

• 问题的setting
  • 在图上进行节点分类，其中只有一部分节点有label        
  • ——>基于图的半监督学习
  • 传统的方法是使用平滑正则
    • 
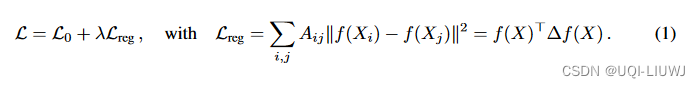
      • 其中L0表示图中有监督部分的loss
      • f是神经网络，Δ=D-A表示unnormalized的拉普拉斯矩阵
    •  这种方式假设相邻的节点有相同/相似的label
      • ——>这种平滑性假设在一定程度上限制了模型的表达能力
  • 论文中直接使用一个神经网络f(X,A)来编码图结构
    • 提取学到的node embedding中，有label的那一部分，计算L0，以此进行训练

2 图卷积的快速估计

• 考虑一个多层的GCN，其中第l层的propagation可以写成
  • 
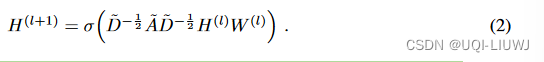
    • ,A是邻接矩阵
    • 
    • W是第l层的可学习参数
    • σ是激活函数
    • 第零层=X

     

  • 论文接下来的部分将说明这种propagation将如何用一阶切比雪夫谱图卷积近似

2.1 谱图卷积

在GNN笔记：图卷积_UQI-LIUWJ的博客-CSDN博客_gnn 多维图卷积中，我们有：

这个就是论文中的 

按照论文的说法，U是normalized 的拉普拉斯矩阵的特征向量矩阵

; 是x在图上的傅里叶变换

而切比雪夫多项式作为谱图卷积的卷积核，在 GCN笔记：Graph Convolution Neural Network，ChebNet_graphconv和gcnconv_UQI-LIUWJ的博客-CSDN博客

中说过（第2节）

这对应的是论文中的 

 2.2 一阶近似

切比雪夫一阶近似的推导，见GCN笔记：Graph Convolution Neural Network，ChebNet_graphconv和gcnconv_UQI-LIUWJ的博客-CSDN博客

第3节

对应的是论文中的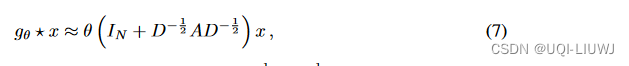 

和

3 半监督点分类

• 记 ，那么（8）可以等价为
• 论文中使用两层GCN
  • 
• 由于问题是一个半监督多类别分类问题，所以最后衡量模型的方式是，对所有有标签的样例，使用交叉熵来进行评估

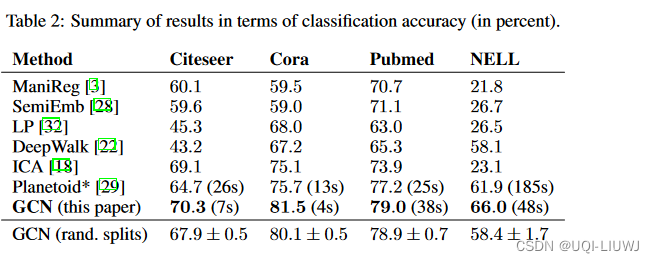
4 实验部分

4.1 数据集

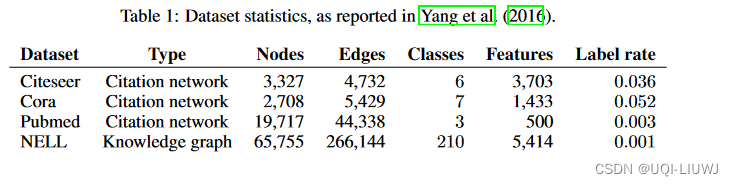
 4.2 结果