KKT条件定义
KKT条件(Karush–Kuhn–Tucker conditions)是最优化(特别是非线性规划)领域最重要的成果之一,是判断某点是极值点的必要条件。
最优化问题
要选择一组参数(变量),在满足一定的限制条件(约束)下,使设计指标(目标)达到最优值。
根据有无约束以及约束特征,可以将最优化问题分为以下三类,每类问题的求解方法也紧跟着列出。
最优化问题分类
无约束优化问题**:直接求导、最速下降法、共轭梯度法、牛顿法等;
等式约束优化问题:拉格朗日(Lagrange)乘数法;
不等式约束优化问题:**KKT条件。
KKT条件理论部分
如果没有人提出KKT理论,对于不等式约束的优化问题,我们该怎么思考呢?下面是一个小例子:
m i n f ( X ) s . t g ( X ) ≤ 0 min \;\; f(X) \;\; s.t \;\; g(X) \leq 0 minf(X)s.tg(X)≤0
如果是最小化问题,即**minf(X)**,约束改写为**g(X)>=0**的形式(原因后文会解释)。
目前我们会求导也会等式约束下的拉格朗日乘数法
一步步来,先对f(X)函数求导吧(若X多维则是求梯度),即先不考虑g(X)<=0这个约束。
先求导取得f(X)的极小值,然后将极小值那个点对应的x值带入g(x)看看满不满足小于0的这个约束
带入g(X)会出现3个情况
g(X)<0
那正好满足约束,X*就是我们要找的最优解。
猛然发现,此时该约束完全不起作用啊(称为不起作用约束),毕竟我们计算X*时压根都没考虑它。
=0
也就是最优解X*正好也让约束取了等号。
转化为含有等式约束的优化问题。拉格朗日乘数法
>0
显然此时的X*不满足约束,应舍弃。
接下来只用考虑<0和=0的情况
如果<0则是约束不起作用,转化为无约束优化问题
=0则是用拉格朗日乘数法来求解

可以分类讨论但是数学家追求形式的大一统
既然都已经引进拉格朗日乘子λ了,那也得想办法使得在g(X*)<0情形下,也要与λ有点关系。
考虑到若g(X*)<0,此时该约束不起作用,而已经构造好的拉格朗日函数中又有λ,怎么办?
很简单,让拉格朗日函数中的λ=0即可!此时拉格朗日函数可不就简化为L(x, λ)=f(X)了嘛。此时对L(x, λ)求导(等价于对f(X)求导)时既不用管约束,也没有λ的干扰,简直完美。
总结一下就是
(1)若g(X*)=0,引入拉格朗日乘子λ,并要求λ≥0;
(2)若g(X*)<0,要求λ=0。
发现可以采用λg(X*)=0的形式统一了!!!牛逼啊!!!
KKT条件的数学公式
仅有一个不等式约束的KKT条件


式(1):对拉格朗日函数求梯度(若X一维就是求导),其中,下三角表示梯度;
式(2):核心公式,要么λ=0,要么g(X*)=0(此处要求两者不能同时为0);
式(3):拉格朗日乘子λ必须是正的(下一部分的图示法有证明);
式(4):原问题自己的约束。
可见,式(1)和(2)都是等式,可以帮助我们求最优X*和λ,因为式(2)要分类讨论,所以可能存在多个X*和λ;式(3)和(4)主要起验证作用,帮助我们排除掉一些不满足式(3)和(4)的X*和λ。
具体地,在应用KKT条件计算时,通常也是分类讨论后先求解X*和λ,再验证其是否满足式(3)和(4),从而排除一些解。
像上述仅含有一个约束的例子,只需要分两类,通常是以拉格朗日乘子λ是否为0进行分类:
(1) 当 λ=0 时,计算X的值,并验证g(X)≤0是否成立;
(2) 当 λ≠0 时,计算X和λ的值,并验证g(X)≤0和λ≥0是否成立。
含有多个多个等式约束和不等式约束的情况

此时的拉格朗日函数为:

其中,**{λi}指的是一系列的λ(有m个),同理{μj}**也是。由于是多个约束,因此引入求和号∑。
其对应的KKT条件为:

利用式(1)(2)(3)求最优X*和 λi,然后通过式(4)和(5)验证这些解是否可行,“可行”指的是这些解是否能让(4)和(5)的不等号成立,不成立则排除。注意,μj是可以取任意值的,不受限制。因为它们是等式约束的拉格朗日乘子,不是不等式的乘子。
由于该问题有m个不等式约束,每个约束对应的拉格朗日/KKT乘子λi都可以“=0”或“≠0”。因此,需要分类讨论的情况有2^m种。
分类详情如下:(1) 当λ1=0,λ2≠0,…,λm≠0时;(2) 当λ1=0,λ2=0,…,λm≠0时;。。。。。。
总结:
能解出最优解的一定是等式,故式(1)(2)(3)帮我们求最优解;
式(4)和式(5)是不等式,帮我们排除一些解,或者得到最优解的适用范围。
得到最优解的适用范围”这句话,其主要针对符号运算的情形
大家在写论文时,建立的数学模型多是用参数和变量表示的,不同情形下的最优解也是符号表达式,因此很难比较大小。
此时,只能通过式(4)和(5),来得到在什么条件(某符号表达式满足某条件)下,最优解X*和对应的f(X*)值为多少,即需要分类讨论。
KKT补充条件
充分性和必要性说明
KKT条件是判断某点是极值点的必要条件,不是充分条件。换句话说,最优解一定满足KKT条件,但KKT条件的解不一定是最优解。
对于凸规划,KKT条件就是充要条件了,只要满足KKT条件,则一定是极值点,且得到的一定还是全局最优解。
凸规划指的是:目标函数为凸函数,不等式约束函数也为凸函数,等式约束函数是仿射的(理解成是线性的也行)。这牵扯到另一个领域了,本文不再展开陈述。
补充:凸规划/凸优化只研究凸函数的最小化问题,并且认为凹函数的最大化问题是与它等价的。毕竟凹函数只需加个负号就是凸函数了,所以在研究问题中,就不再提凹函数了。
Min/Max与“≤0”和“≥0”的规定
(1)如果目标为最小化(Min)问题,那么不等式约束需要整理成“≤0”的形式;
(2)如果目标为最大化(Max)问题,那么不等式约束需要整理成“≥0”的形式;
以仅含有一个不等式约束的情形为例,最小化和最大化的优化问题要整理成如下形式:

该形式可以死记硬背,但时间一长,大家可能会忘记或记混了,下面,采用图示法逐步展示为什么会有这个要求,该分析过程也展现了KTT条件的几何思想。

上图画出了3条f(X)函数的等值线(图中虚线),以及右下角为可行域S(即约束条件规定的区域)和g(X)=0的曲线,最优解为X*。基于此,具体分析如下:
(1)f(X)函数值下降方向为左上方:
目标是最小化问题,若下降方向为右下方,则最优解(图中X*)一定不是在g(X)=0上,而是在可行域S内部;
由于KKT条件中第一条就需要计算f(X)和g(X)函数的梯度,所以,这里补充一个基础知识:梯度方向垂直于函数等值线,指向函数值增长的方向。
基于此,我们尝试画出f(X)和g(X)函数的梯度方向:
(2)画出f(X)的梯度方向(下图红色方向):
梯度方向是函数值增长的方向,因此指向右下方;负梯度方向是函数值下降的方向,指向左上方;
(3)画出g(X)的梯度方向(下图蓝色方向):
由于曲线是g(X)=0,右下方是g(X)<0,是在下降,因此,g(X)函数值增长的方向就是左上方了。

由上述分析和上图可知,在最优解X*处,f(X*)和g(X*)的梯度方向共线且方向相反。向量共线且方向相反在数学上的写法就是:
负梯度向量是另一个梯度向量的λ倍。移项后发现,这不就是KKT条件的第一个等式嘛!
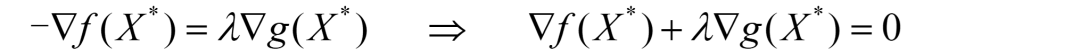
同时可知,λ的值只能取正值,因为g(X)的梯度方向与f(X)负梯度方向相同。这也是KKT条件要求 λ≥0 的原因。
基于以上分析可知:最小化问题的约束条件应该整理成“≤0”的形式,且λ≥0。
同理,最大化的分析不再展开,仅给出分析图

补充一点,请问大家,对于最大化问题,如果可行域也非要写成g(X)≤0的形式,能行吗?先别忙着否定,我们分析一下。
此时g(X*)的梯度方向就不再是右下方了(不是上图了),而是f(X*)与g(X*)的梯度方向相同,有:

此时如上图,要么KKT条件第一项改为“作差”,要么让λ<0。无论哪一个,其实都是徒增烦恼。不如上来就规定约束写成g(X)≥0来的方便。
多约束条件情形
仅是把梯度的共线变为梯度的线性组合
假设有起作用约束g1(X)和起作用约束g2(X)共同影响目标函数f(X)的梯度,又是怎么样的图形呢?

我们分别画出g1(X)函数在X处的梯度,如图中蓝色向量,其垂直于曲线g1(X)=0;同理,画出g2(X)函数在X*处的梯度,是另一个蓝色向量。
至于f(X)函数的梯度,图中画出负梯度方向(函数值下降的方向),这样画的好处是可以直观地看出三个梯度向量间的关系:
函数的负梯度可以表示成g1函数和g2函数梯度的线性组合。则有如下公式:可以用向量表示

简单移项后,又发现了我们的老朋友:KKT条件的第一个等式。从图中也可以看出,梯度向量之间的夹角为锐角,因此也有λ1≥0,λ2≥0的要求。