求导，积分

news2024/11/23 23:55:30

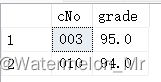
求导公式：

复合函数求导法则：两个函数导函数的乘积.
例如：f(x)=2x+1,f'(x)=2,g(x)=x^2+4x+4,g'(x)=2x+4
那么复合函数：
g(f(x))=(2x+1)^2+4(2x+1)+4
把（2x+1）看做整体,则g'=2(2x+1)+4
然后再求（2x+1）的导函数,为：2
于是最后的结果为：2(2(2x+1)+4)=8x+12

积分公式：

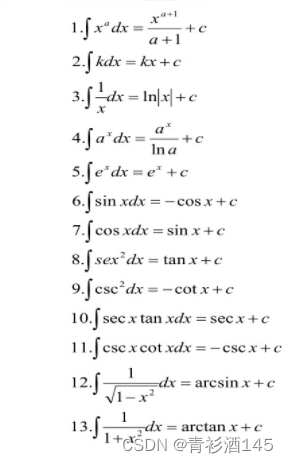
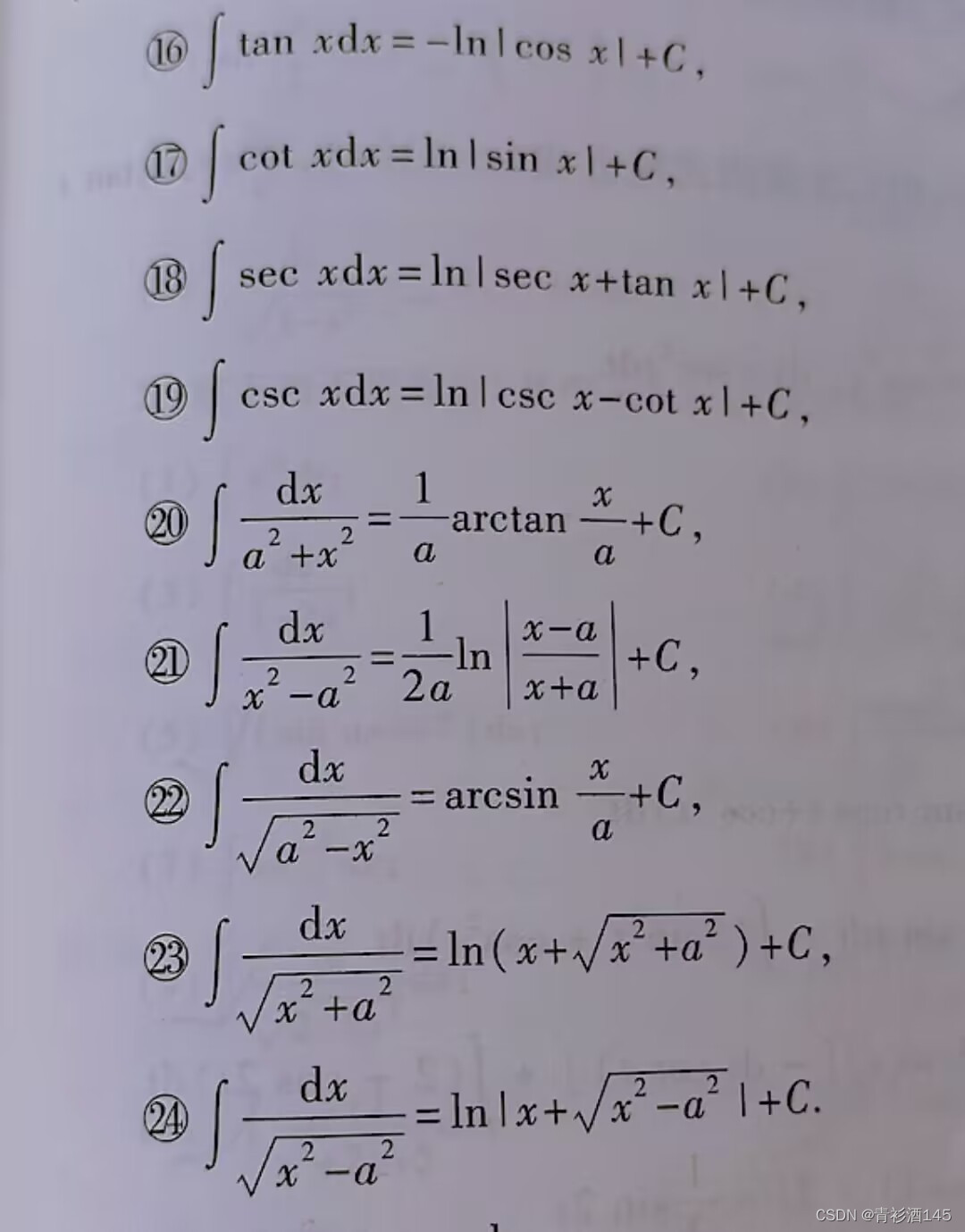
函数和的积分等于分别的积分和，对于乘常数，可以把常数提出来

对于一个式子考虑能否分项（分成两个数的和），抄分母，加一个减一个

$\int \frac{1}{x^{4}\left ( x^{2}+1 \right)}dx=\int \frac{1+x^{2}-x^{2}}{x^{4}\left ( x^{2}+1 \right)}dx=\int \frac{1}{x^{4}}dx-\int\frac{1+x^{2}-x^{2}}{x^{2}(x^{2}+1)}$

第一类换元法：

$dy={y}'*dx\Rightarrow {u}'*dx=du \left \{ u=f(x) \right \} \Rightarrow du={u}'*dx$

去原式子里找f(u)和u的倒数的乘积，然后对dx凑微分到du等于（缺少常数的话可以自己补）

$\int \frac{1}{\sqrt{a^{2}-x^{2}}}dx(a>0)=\int \frac{1}{\sqrt{1-(\frac{x}{a})^2}}\frac{1}{a}dx=\int \frac{1}{\sqrt{1-(\frac{x}{a})^2}}d\frac{x}{a}=arcsin\frac{x}{a}+c$

$\frac{1}{\sqrt{x}}dx=2d\sqrt{x}$

先凑出u，然后用u积分，最后再将结果的u换成x

第二类换元法：

直接换元

$(sinx)^{2}+(cosx)^{2}=1,(tanx)^2+1=(secx)^2$

对于三角函数可以画辅助三角形

分部积分法：

${(u(x)v(x))}'={u}'(x)v(x)+u(x){v}'(x)\Rightarrow u{v}'={(uv)}'-{u}'v\Rightarrow \int u{v}'dx=\int {(uv)}'dx -\int {u}'vdx\Rightarrow \int u{v}'dx=uv-\int {u}'vdx$

反对幂指三原则

反对不容易积分，让其求导，指三容易积分，让其积分

有口诀：

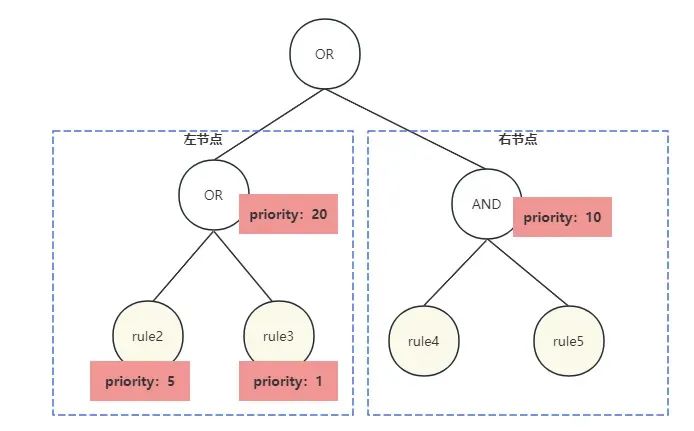
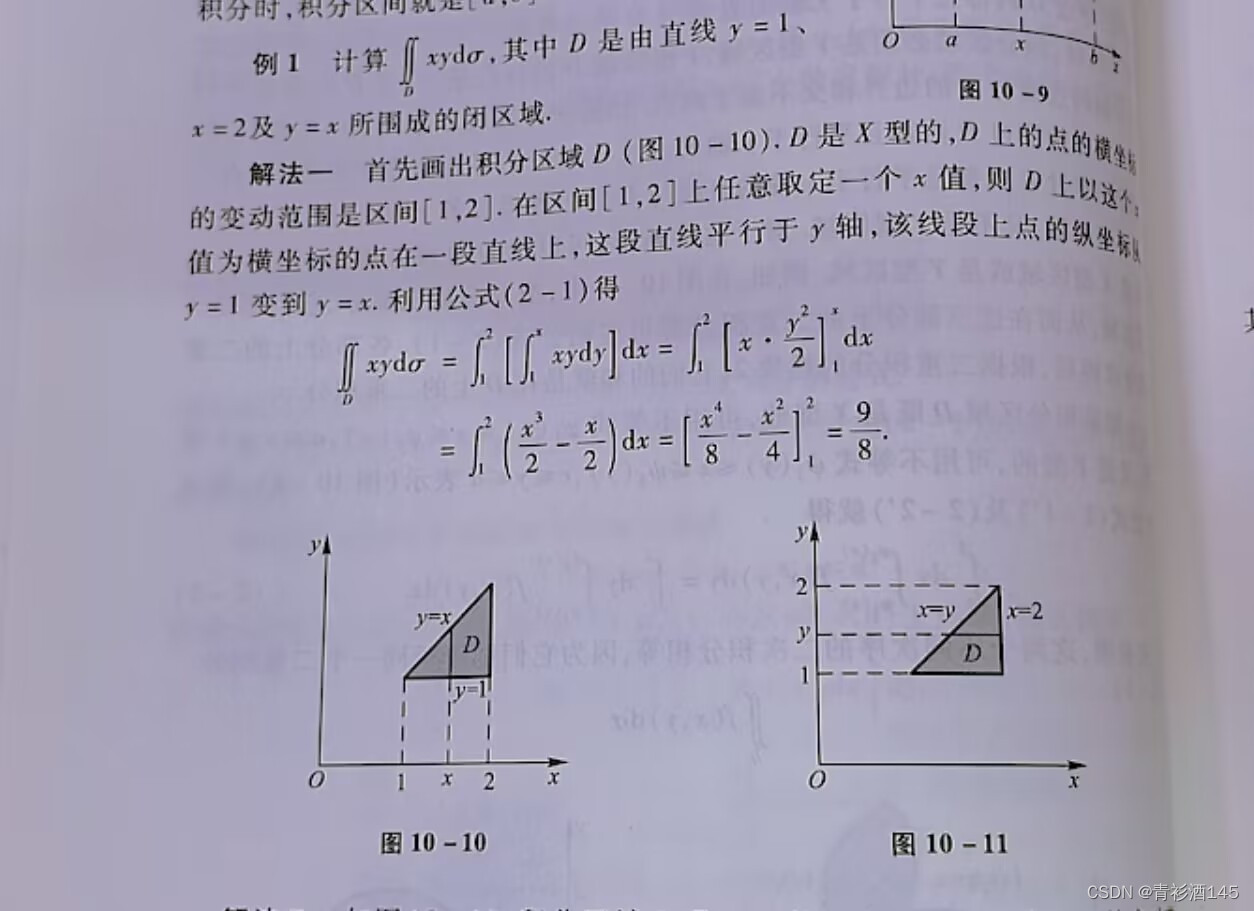
二重积分的计算

先确定外层积分是x轴还是y轴。如果外层是x轴，那么内层的x对于y的积分就是常数，先将图形的x轴坐标范围确定为外层定积分的上下限，再做一条平行y轴的辅助线确定y坐标的上下限作为内层积分的上下限。

极坐标下的二重积分

区域为圆或者表达式为圆是用极坐标,对于圆点不在原点的时候，可以用极坐标平移的办法

$x=rcos\theta ,y=rsin\theta ,x^2+y^2=r^2$ ，这里的r是极径。

对于区域D： $x^2+y^2-2x-2y<=0\Rightarrow r^2<=2(sin\theta +cos\vartheta )$ ,如果要求极径为0时的 $\theta$ 是多少，带入上式子得 $sin\theta +cos\theta =0\Rightarrow tan\theta =-1$ 。