矩阵微积分(Matrix Calculus)
在开始之前,需要先了解矩阵微积分的一些计算规则。
首先,对于矩阵微积分的表示,通常由两种符号约定:
-
分母布局
-
标量关于向量的导数为列向量
-
向量关于标量的导数为行向量
-
N维向量对M维向量的导数为M*N维矩阵(雅可比矩阵的转置)

-
标量对M维向量的二阶偏导数为M*M维矩阵(Hessian矩阵,也写作 ▽ 2 f ( x ) \triangledown^2f(x) ▽2f(x),第m行第n个元素为 ∂ 2 y ∂ x m ∂ x n \frac{\partial^2y}{\partial x_m\partial x_n} ∂xm∂xn∂2y)
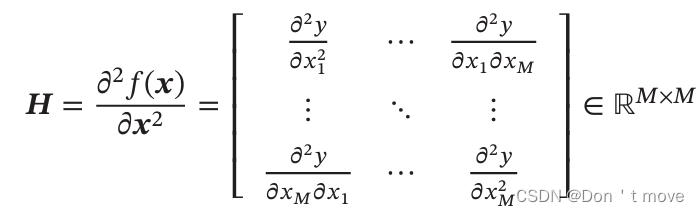
-
-
分子布局
- 标量关于向量的导数为行向量
- 向量关于标量的导数为列向量
- N维向量对于M维向量的导数为N*M维矩阵(雅可比矩阵)
∂ f ( x ) ∂ x = [ ∂ y 1 ∂ x 1 ⋯ ∂ y 1 ∂ x M ⋮ ⋱ ⋮ ∂ y N ∂ x 1 ⋯ ∂ y N ∂ x M ] ∈ R N × M \begin{aligned} \frac{\partial f(x)}{\partial x}= \begin{bmatrix} \frac{\partial y_1}{\partial x_1}&\cdots&\frac{\partial y_1}{\partial x_M}\\ \vdots&\ddots&\vdots\\ \frac{\partial y_N}{\partial x_1}&\cdots&\frac{\partial y_N}{\partial x_M} \end{bmatrix}\in\mathbb{R}^{N\times M} \end{aligned} ∂x∂f(x)= ∂x1∂y1⋮∂x1∂yN⋯⋱⋯∂xM∂y1⋮∂xM∂yN ∈RN×M
- 标量对M维向量的二阶偏导数为M*M维矩阵(Hessian矩阵的转置)
∂
2
y
∂
x
2
=
∂
∂
x
∂
y
∂
x
=
∂
∂
x
[
∂
y
∂
x
1
⋯
∂
y
∂
x
M
]
=
[
∂
2
y
∂
x
1
2
⋯
∂
2
y
∂
x
M
∂
x
1
⋮
⋱
⋮
∂
2
y
∂
x
1
∂
x
M
⋯
∂
2
y
∂
x
M
2
]
∈
R
M
×
M
\begin{aligned} \frac{\partial^2y}{\partial x^2} &=\frac{\partial}{\partial x}\frac{\partial y}{\partial x}\\ &=\frac{\partial}{\partial x} \begin{bmatrix} \frac{\partial y}{\partial x_1}&\cdots&\frac{\partial y}{\partial x_M} \end{bmatrix}\\ &=\begin{bmatrix} \frac{\partial^2 y}{\partial x_1^2}&\cdots&\frac{\partial^2 y}{\partial x_M\partial x_1}\\ \vdots&\ddots&\vdots\\ \frac{\partial^2 y}{\partial x_1\partial x_M}&\cdots&\frac{\partial^2 y}{\partial x_M^2} \end{bmatrix} \in\mathbb{R}^{M\times M} \end{aligned}
∂x2∂2y=∂x∂∂x∂y=∂x∂[∂x1∂y⋯∂xM∂y]=
∂x12∂2y⋮∂x1∂xM∂2y⋯⋱⋯∂xM∂x1∂2y⋮∂xM2∂2y
∈RM×M
分子布局和分母布局之间是转置的关系。本系列所有内容默认都以分母布局进行计算和解释。
矩阵微积分也遵从链式法则(分母布局)
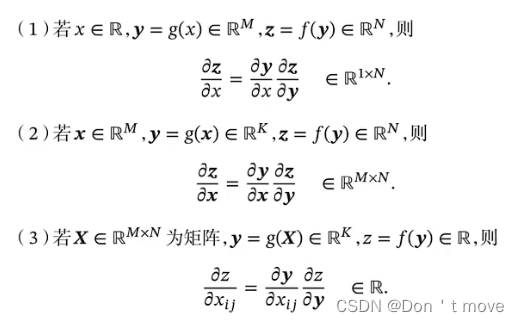
梯度计算
前馈神经网络的结构化风险函数:
R
(
W
,
b
)
=
1
N
∑
n
=
1
N
L
(
y
(
n
)
,
y
^
(
n
)
)
+
1
2
λ
∥
W
∥
F
2
\mathcal{R}(W,b)=\frac{1}{N}\sum_{n=1}^N\mathcal{L}(y^{(n)},\hat{y}^{(n)})+\frac{1}{2}\lambda\|W\|_F^2
R(W,b)=N1n=1∑NL(y(n),y^(n))+21λ∥W∥F2
先分别计算网络中的某一层的损失函数
L
\mathcal{L}
L对参数的导数(分母布局),利用链式法则
∂
L
(
y
,
y
^
)
∂
w
i
j
(
l
)
=
∂
L
(
y
,
y
^
)
∂
z
(
l
)
∂
z
(
l
)
∂
w
i
j
(
l
)
∂
L
(
y
,
y
^
)
∂
b
(
l
)
=
∂
L
(
y
,
y
^
)
∂
z
(
l
)
∂
z
(
l
)
∂
b
(
l
)
\begin{aligned} \frac{\partial \mathcal{L}(y,\hat{y})}{\partial w_{ij}^{(l)}} &=\frac{\partial \mathcal{L}(y,\hat{y})}{\partial z^{(l)}}\frac{\partial z^{(l)}}{\partial w_{ij}^{(l)}}\\ \frac{\partial \mathcal{L}(y,\hat{y})}{\partial b^{(l)}} &=\frac{\partial \mathcal{L}(y,\hat{y})}{\partial z^{(l)}}\frac{\partial z^{(l)}}{\partial b^{(l)}}\\ \end{aligned}
∂wij(l)∂L(y,y^)∂b(l)∂L(y,y^)=∂z(l)∂L(y,y^)∂wij(l)∂z(l)=∂z(l)∂L(y,y^)∂b(l)∂z(l)
其中
z
(
l
)
=
W
(
l
)
a
(
l
−
1
)
+
b
(
l
)
z^{(l)}=W^{(l)}a^{(l-1)}+b^{(l)}
z(l)=W(l)a(l−1)+b(l)是一个向量,根据分母布局的规则,向量对于标量求导为行向量,因此
∂
z
(
l
)
∂
w
i
j
(
l
)
\frac{\partial z^{(l)}}{\partial w_{ij}^{(l)}}
∂wij(l)∂z(l)为行向量
∂
z
(
l
)
∂
w
i
j
(
l
)
=
[
∂
z
1
(
l
)
∂
w
i
j
(
l
)
⋯
∂
z
i
(
l
)
∂
w
i
j
(
l
)
⋯
∂
z
M
l
(
l
)
∂
w
i
j
(
l
)
]
=
[
∂
(
w
1
j
(
l
)
a
(
l
−
1
)
+
b
i
(
l
)
)
∂
w
i
j
(
l
)
⋯
∂
(
w
i
j
(
l
)
a
(
l
−
1
)
+
b
i
(
l
)
)
∂
w
i
j
(
l
)
⋯
∂
(
w
M
i
j
(
l
)
a
(
l
−
1
)
+
b
i
(
l
)
)
∂
w
i
j
(
l
)
]
=
[
0
⋯
a
j
(
l
−
1
)
⋯
0
]
≜
l
i
(
a
j
(
l
−
1
)
)
∈
R
1
×
M
l
\begin{aligned} \frac{\partial z^{(l)}}{\partial w_{ij}^{(l)}} &=\begin{bmatrix} \frac{\partial z_1^{(l)}}{\partial w_{ij}^{(l)}}& \cdots& \frac{\partial z_i^{(l)}}{\partial w_{ij}^{(l)}}& \cdots& \frac{\partial z_{M_l}^{(l)}}{\partial w_{ij}^{(l)}} \end{bmatrix}\\ &=\begin{bmatrix} \frac{\partial (w_{1j}^{(l)}a^{(l-1)}+b_i^{(l)})}{\partial w_{ij}^{(l)}}& \cdots& \frac{\partial (w_{ij}^{(l)}a^{(l-1)}+b_i^{(l)})}{\partial w_{ij}^{(l)}}& \cdots& \frac{\partial (w_{M_ij}^{(l)}a^{(l-1)}+b_i^{(l)})}{\partial w_{ij}^{(l)}} \end{bmatrix}\\ &=\begin{bmatrix} 0&\cdots&a_j^{(l-1)}&\cdots&0 \end{bmatrix}\\ &\triangleq\mathbb{l}_i(a_j^{(l-1)})\in\mathbb{R}^{1\times M_l} \end{aligned}
∂wij(l)∂z(l)=[∂wij(l)∂z1(l)⋯∂wij(l)∂zi(l)⋯∂wij(l)∂zMl(l)]=[∂wij(l)∂(w1j(l)a(l−1)+bi(l))⋯∂wij(l)∂(wij(l)a(l−1)+bi(l))⋯∂wij(l)∂(wMij(l)a(l−1)+bi(l))]=[0⋯aj(l−1)⋯0]≜li(aj(l−1))∈R1×Ml
同样,向量
z
(
l
)
z^{(l)}
z(l)对向量
b
(
l
)
b^{(l)}
b(l)的导数为
∂
z
(
l
)
∂
b
(
l
)
=
[
∂
(
w
1
j
(
l
)
a
(
l
−
1
)
+
b
1
(
l
)
)
∂
b
1
(
l
)
⋯
∂
(
w
M
i
j
(
l
)
a
(
l
−
1
)
+
b
i
(
l
)
)
∂
b
1
(
l
)
⋮
⋱
⋮
∂
(
w
1
j
(
l
)
a
(
l
−
1
)
+
b
1
(
l
)
)
∂
b
M
i
(
l
)
⋯
∂
(
w
M
i
j
(
l
)
a
(
l
−
1
)
+
b
i
(
l
)
)
∂
b
M
i
(
l
)
]
=
[
1
⋯
0
⋮
⋱
⋮
0
⋯
1
]
=
I
M
i
∈
R
M
l
×
M
l
\begin{aligned} \frac{\partial z^{(l)}}{\partial b^{(l)}} &=\begin{bmatrix} \frac{\partial(w_{1j}^{(l)}a^{(l-1)}+b_1^{(l)})}{\partial b_1^{(l)}}&\cdots&\frac{\partial(w_{M_ij}^{(l)}a^{(l-1)}+b_i^{(l)})}{\partial b_1^{(l)}}\\ \vdots&\ddots&\vdots\\ \frac{\partial(w_{1j}^{(l)}a^{(l-1)}+b_1^{(l)})}{\partial b_{M_i}^{(l)}}&\cdots&\frac{\partial(w_{M_ij}^{(l)}a^{(l-1)}+b_i^{(l)})}{\partial b_{M_i}^{(l)}} \end{bmatrix}\\ &=\begin{bmatrix} 1&\cdots&0\\ \vdots&\ddots&\vdots\\ 0&\cdots&1 \end{bmatrix}\\ &=I_{M_i}\in\mathbb{R}^{M_l\times M_l} \end{aligned}
∂b(l)∂z(l)=
∂b1(l)∂(w1j(l)a(l−1)+b1(l))⋮∂bMi(l)∂(w1j(l)a(l−1)+b1(l))⋯⋱⋯∂b1(l)∂(wMij(l)a(l−1)+bi(l))⋮∂bMi(l)∂(wMij(l)a(l−1)+bi(l))
=
1⋮0⋯⋱⋯0⋮1
=IMi∈RMl×Ml
除了上面计算的计算部分外,还剩下关键的一项
∂
R
(
y
,
y
^
)
∂
z
(
l
)
\frac{\partial\mathcal{R}(y,\hat{y})}{\partial z^{(l)}}
∂z(l)∂R(y,y^),这一项叫第
l
l
l层的误差项
δ
(
l
)
\delta^{(l)}
δ(l),同样,再次应用链式法则进行计算
δ
(
l
)
≜
∂
L
(
y
,
y
^
)
∂
z
(
l
)
=
∂
L
(
y
,
y
^
)
∂
z
(
l
+
1
)
∂
z
(
l
+
1
)
∂
a
(
l
)
∂
a
(
l
)
∂
z
(
l
)
\begin{aligned} \delta^{(l)}&\triangleq\frac{\partial \mathcal{L}(y,\hat{y})}{\partial z^{(l)}}\\ &=\frac{\partial\mathcal{L}(y,\hat{y})}{\partial z^{(l+1)}}\frac{\partial z^{(l+1)}}{\partial a^{(l)}}\frac{\partial a^{(l)}}{\partial z^{(l)}}\\ \end{aligned}
δ(l)≜∂z(l)∂L(y,y^)=∂z(l+1)∂L(y,y^)∂a(l)∂z(l+1)∂z(l)∂a(l)
其中可直接得到
∂
L
(
y
,
y
^
)
∂
z
(
l
+
1
)
=
δ
(
l
+
1
)
∂
z
(
l
+
1
)
∂
a
(
l
)
=
(
W
(
l
+
1
)
)
T
\begin{aligned} &\frac{\partial\mathcal{L}(y,\hat{y})}{\partial z^{(l+1)}}=\delta^{(l+1)}\\ &\frac{\partial z^{(l+1)}}{\partial a^{(l)}}=(W^{(l+1)})^T \end{aligned}
∂z(l+1)∂L(y,y^)=δ(l+1)∂a(l)∂z(l+1)=(W(l+1))T
剩下一项计算计算如下
∂
a
(
l
)
∂
z
(
l
)
=
∂
f
l
(
z
(
l
)
)
∂
z
(
l
)
=
[
∂
f
l
(
z
1
(
l
)
)
∂
z
1
(
l
)
⋯
∂
f
l
(
z
M
l
(
l
)
)
∂
z
1
(
l
)
⋮
⋱
⋮
∂
f
l
(
z
1
(
l
)
)
∂
z
M
l
(
l
)
⋯
∂
f
l
(
z
M
l
(
l
)
)
∂
z
M
l
(
l
)
]
=
[
f
l
′
(
z
1
(
l
)
)
⋯
0
⋮
⋱
⋮
0
⋯
f
l
′
(
z
M
l
(
l
)
)
]
=
d
i
a
g
(
f
l
′
(
z
(
l
)
)
)
\begin{aligned} \frac{\partial a^{(l)}}{\partial z^{(l)}}&=\frac{\partial f_l(z^{(l)})}{\partial z^{(l)}}\\ &=\begin{bmatrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_1^{(l)}}\\ \vdots&\ddots&\vdots\\ \frac{\partial f_l(z_1^{(l)})}{\partial z_{M_l}^{(l)}}&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}} \end{bmatrix}\\ &=\begin{bmatrix} f_l^\prime(z_1^{(l)})&\cdots&0\\ \vdots&\ddots&\vdots\\ 0&\cdots&f_l^\prime(z_{M_l}^{(l)}) \end{bmatrix}\\ &=\mathrm{diag}(f_l^\prime(z^{(l)})) \end{aligned}
∂z(l)∂a(l)=∂z(l)∂fl(z(l))=
∂z1(l)∂fl(z1(l))⋮∂zMl(l)∂fl(z1(l))⋯⋱⋯∂z1(l)∂fl(zMl(l))⋮∂zMl(l)∂fl(zMl(l))
=
fl′(z1(l))⋮0⋯⋱⋯0⋮fl′(zMl(l))
=diag(fl′(z(l)))
因此
δ
(
l
)
=
δ
(
l
+
1
)
(
W
(
l
+
1
)
)
T
d
i
a
g
(
f
l
′
(
z
(
l
)
)
)
=
(
δ
(
l
+
1
)
(
W
(
l
+
1
)
)
T
)
⊙
f
l
′
(
z
(
l
)
)
∈
R
M
l
\begin{aligned} \delta^{(l)} &=\delta^{(l+1)}(W^{(l+1)})^T\mathrm{diag}(f_l^\prime(z^{(l)}))\\ &=(\delta^{(l+1)}(W^{(l+1)})^T)\odot f_l^\prime(z^{(l)})\in\mathbb{R}^{M_l} \end{aligned}
δ(l)=δ(l+1)(W(l+1))Tdiag(fl′(z(l)))=(δ(l+1)(W(l+1))T)⊙fl′(z(l))∈RMl
符号
⊙
\odot
⊙表示对应位置元素相乘1。从上式中可以看出,第
l
l
l层的误差项可以由第
l
+
1
l+1
l+1层的误差项乘以对应的权重矩阵的转置再乘以对应项激活函数的导数来得到,这个过程就是所谓的反向传播。也就是说,要计算对任意一个参数的偏导数,要从神经网络最后一层先计算出损失函数对最后一层净活性值的偏导数,即误差项
δ
(
L
)
=
∂
L
∂
z
(
L
)
\delta^{(L)}=\frac{\partial \mathcal{L}}{\partial z^{(L)}}
δ(L)=∂z(L)∂L,然后根据上式一层一层向前计算
再带回之前的式子,得到最终梯度为:
∂
L
(
y
,
y
^
)
∂
w
i
j
(
l
)
=
δ
(
l
)
l
i
(
a
j
(
l
−
1
)
)
=
[
δ
1
(
l
)
⋯
δ
i
(
l
)
⋯
δ
M
l
(
l
)
]
[
0
⋯
a
j
(
l
−
1
)
⋯
0
]
T
=
δ
i
(
l
)
a
j
(
l
−
1
)
⇒
∂
L
(
y
,
y
^
)
∂
W
(
l
)
=
δ
(
l
)
(
a
(
l
−
1
)
)
T
∈
R
M
l
×
M
l
−
1
\begin{aligned} \frac{\partial\mathcal{L}(y,\hat{y})}{\partial w_{ij}^{(l)}} &=\delta^{(l)}\mathbb{l}_i(a_j^{(l-1)})\\ &=\begin{bmatrix}\delta_1^{(l)}&\cdots&\delta_i^{(l)}&\cdots&\delta_{M_l}^{(l)}\end{bmatrix}\begin{bmatrix}0&\cdots&a_j^{(l-1)}&\cdots&0\end{bmatrix}^T\\ &=\delta_i^{(l)}a_j^{(l-1)}\\ \Rightarrow\frac{\partial\mathcal{L}(y,\hat{y})}{\partial W^{(l)}} &=\delta^{(l)}(a^{(l-1)})^T\in\mathbb{R}^{M_l\times M_{l-1}} \end{aligned}
∂wij(l)∂L(y,y^)⇒∂W(l)∂L(y,y^)=δ(l)li(aj(l−1))=[δ1(l)⋯δi(l)⋯δMl(l)][0⋯aj(l−1)⋯0]T=δi(l)aj(l−1)=δ(l)(a(l−1))T∈RMl×Ml−1
∂
L
(
y
,
y
^
)
∂
b
(
l
)
=
δ
(
l
)
∈
R
M
l
\frac{\partial \mathcal{L}(y,\hat{y})}{\partial b^{(l)}}=\delta^{(l)}\in\mathbb{R}^{M_l}
∂b(l)∂L(y,y^)=δ(l)∈RMl
反向传播算法的伪代码描述

计算机视觉领域(CV)论文中“圈加”、“圈乘”和“点乘”的解释以及代码示例(⊕、⊙、⊗、广播、广播机制、element-wise、矩阵、乘法、矩阵乘法、向量)_圈×-CSDN博客 ↩︎