---

1.最长递增子序列

1.题目链接

• 最长递增子序列

---

2.算法原理详解

• 基本思想：

  • 动态规划
  • 二分查找

• 动态规划思路：

  • 状态表示：以i位置的元素为结尾的所有的子序列中，最长递增子序列的长度
  • 状态转移方程：dp[i] = max(dp[j] + 1) (j < i && nums[j] < nums[i])
  • 该思路中，并不关心该序列长什么样子，只在乎”最后一个元素”是谁

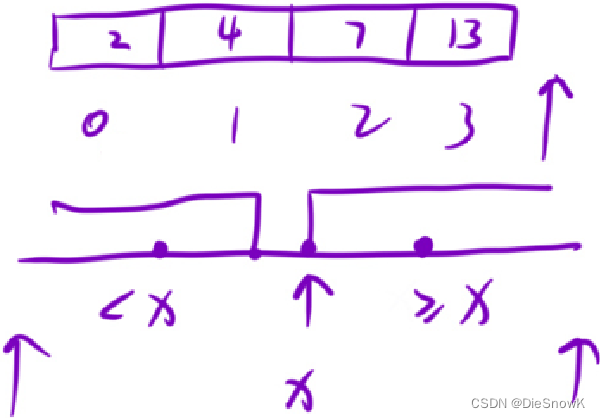
• 贪心优化：

  • 存什么；所有长度为x的递增子序列中，最后一个元素的最小值
  • 存哪里：所有大于等于nums[i]的最小值的位置
    

• 利用二分优化：时间复杂度：$O(N)$ -> $O(lo{g}_N)$
  

---

3.代码实现

int lengthOfLIS(vector<int>& nums) 
{
    int n = nums.size();
    vector<int> ret;
    ret.push_back(nums[0]);

    for(int i = 1; i < n; i++)
    {
        if(nums[i] > ret.back())
        {
            ret.push_back(nums[i]);
        }
        else
        {
            // 二分插入位置
            int left = 0, right = ret.size() - 1;
            while(left < right)
            {
                int mid = left + (right - left) / 2;
                if(ret[mid] < nums[i])
                {
                    left = mid + 1;
                }
                else
                {
                    right = mid;
                }
            }

            ret[left] = nums[i];
        }
    }

    return ret.size();
}

---

2.递增的三元子序列

1.题目链接

• 递增的三元子序列

---

2.算法原理详解

• 本题的贪心策略和最长递增子序列一样
  • 但是本题只需两个变量即可完成贪心，无需数组
    

---

3.题目链接

bool increasingTriplet(vector<int>& nums) 
{
    int a = nums[0], b = INT_MAX;
    for(int i = 1; i < nums.size(); i++)
    {
        if(nums[i] > b)
        {
            return true;
        }
        else if(nums[i] > a)
        {
            b = nums[i];
        }
        else
        {
            a = nums[i];
        }
    }

    return false;
}

---

3.最长连续递增序列

1.题目链接

• 最长连续递增序列

---

2.算法原理详解

• 思路；贪心 + 双指针

---

3.代码实现

int findLengthOfLCIS(vector<int>& nums) 
{
    int n = nums.size(), ret = 0;
    for(int i = 0; i < n; )
    {
        int j = i + 1;
        while(j < n && nums[j - 1] < nums[j])
        {
            j++;
        }

        ret = max(ret, j - i);
        i = j; // 贪心
    }

    return ret;
}

---

4.买卖股票的最佳时机

1.题目链接

• 买卖股票的最佳时机

---

2.算法原理详解

• 思路：贪心 + 一个变量标记“前缀最小值”

---

3.代码实现

int maxProfit(vector<int>& prices) 
{
    int ret = 0, prevMin = INT_MAX;
    for(int i = 0; i < prices.size(); i++)
    {
        if(prices[i] > prevMin)
        {
            ret = max(ret, prices[i] - prevMin);
        }

        prevMin = min(prices[i], prevMin); // 贪心
    }

    return ret;
}

---

5.买卖股票的最佳时机 II

1.题目链接

• 买卖股票的最佳时机 II

---

2.算法原理详解

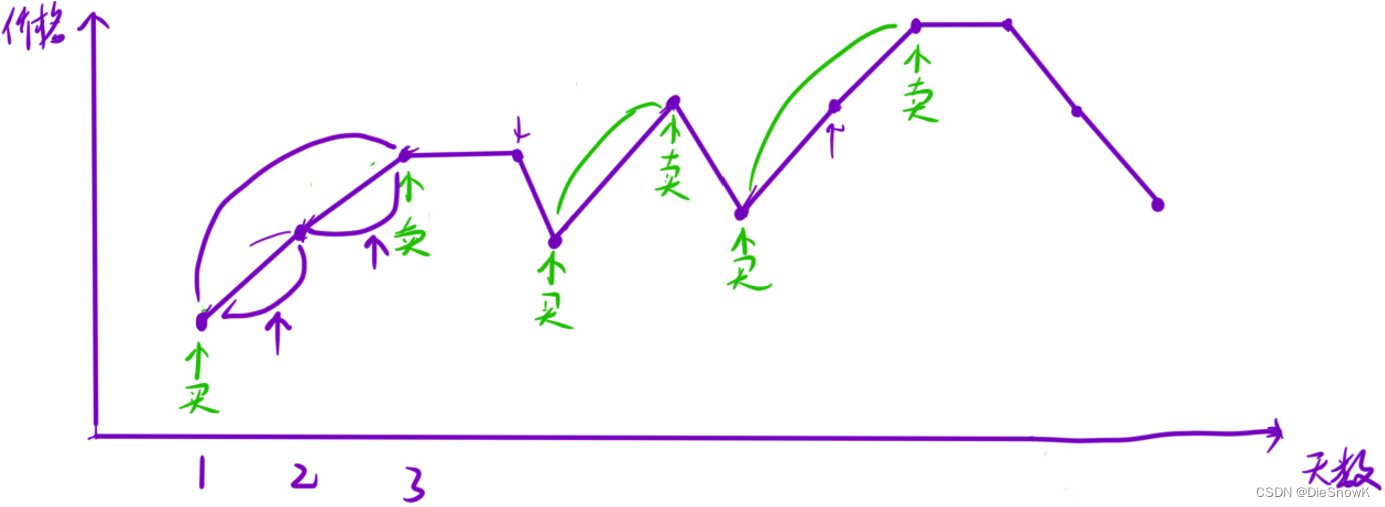
• 贪心：只要能获得正收益，就交易

• 实现一：双指针
  

• 实现二：拆分交易，把交易拆成一天一天
  

---

3.代码实现

// v1.0 双指针
int maxProfit(vector<int>& p) 
{
    int ret = 0, n = p.size();
    for(int i = 0; i < n; i++)
    {
        int j = i;
        while(j + 1 < n && p[j + 1] > p[j])
        {
            j++;
        }

        ret += p[j] - p[i];
        i = j;
    }

    return ret;
}
---------------------------------------------------------
// v2.0 拆分成一天一天
int maxProfit(vector<int>& p) 
{
    int ret = 0;
    for(int i = 1; i < p.size(); i++)
    {
        if(p[i - 1] < p[i])
        {
            ret += p[i] - p[i - 1];
        }
    }

    return ret;
}