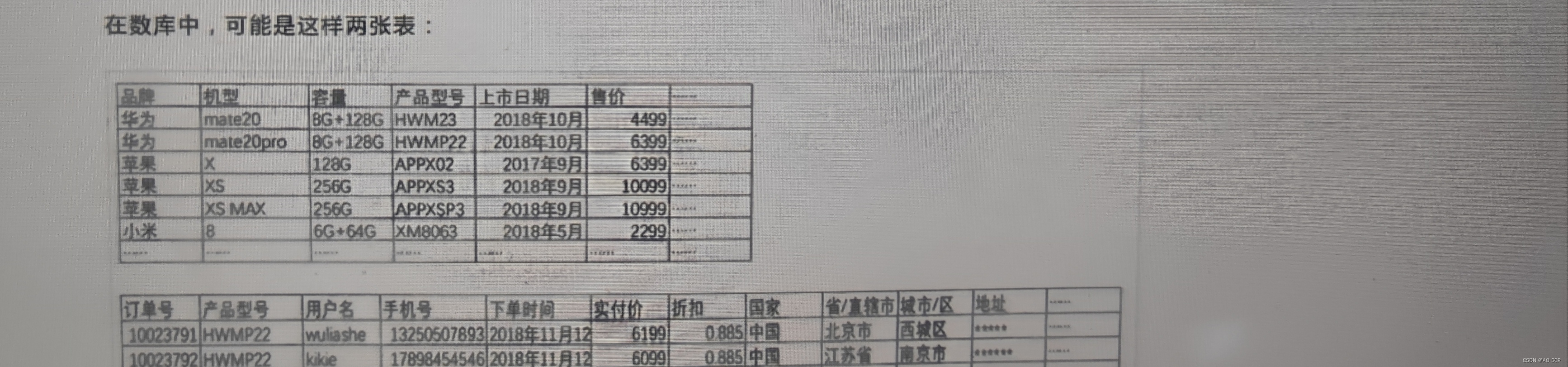
目录
1. 前言
2. 算法流程
3. 代码及仿真结果
3.1 class PolicyIterationPlanner()
3.2 测试代码
3.3 运行结果
3.3.1 价值估计结果
3.3.2 策略迭代得到的最终策略
1. 前言
在强化学习中,根据是否依赖于(环境的)模型,可以分为有模型(model-based)学习和无模型(model-free)学习。根据行动的决策基准,可以分为基于价值的学习(value-based)和基于策略学习(policy-based)。
在基于价值的学习中,根据状态值函数(state-value function)值或者动作值函数的值,进行行动决策。总是选择从当前状态出发可能到达的下一个状态中价值最大的那个状态所对应的行动。
前面两篇分别介绍了直接求解贝尔曼方程进行价值计算以及以迭代的方式求解价值近似(value iteration):
强化学习笔记:基于价值的学习之价值计算(python实现)
强化学习笔记:基于价值的学习之价值迭代(python实现)
本篇进一步介绍基于策略的学习的策略迭代算法原理及其实现。
2. 算法流程
策略迭代包括策略评估(policy evaluation)和策略提升(policy improvement)。
策略评估是指基于当前策略进行值函数评估,本身也是(可以)以迭代的方式求解。基于策略的价值评估应该是要计算价值的期望值,与价值迭代中的价值评估略有不同。但是,由于(如下所示,策略迭代所得到的策略本身是确定性的策略,所以这个期望值也退化成当前策略下最佳行动的价值了)。每次迭代中进行策略评估时,值函数(value function)的初始值是上一个策略(policy)的值函数,这样通常会提高策略评估的收敛速度,这是因为相邻两个策略的值函数改变很小。
策略提升则是指当由策略所得到的行动与基于价值的最佳行动不一致时进行策略更新。
Sutton-book#4.3所给出的策略迭代流程如下所示:

翻成大白话如下所示:
价值和策略初始化:价值初始化为0,各状态下所有各行动的概率指定为相等的概率(虽然初始化为任意值都可以,但是这是最合理的选择)
Iteration直到收敛:
- 基于策略进行状态值评估(期望值):但是,实际上由于策略迭代中的策略是确定性的策略,所以这里的期望值退化成了最佳行动的状态值了。
- 基于状态值最大化准则更新策略。针对每一个状态
- 基于当前策略所得到的行动(即概率最大的那个行动)action_by_policy
- 评估各行动的价值Q(s,a)据此得到行动价值最大的行动best_action_by_value
- 判断两者是否一致(action_by_policy==best_action_by_value?)
- 如果每个状态下的都满足(action_by_policy==best_action_by_value),则停止迭代
- 否则,以贪婪(这个是必然的吗?)的方式更新策略。即将每个状态s下对应最佳行动的policy[s][a]置为1,其余置为0
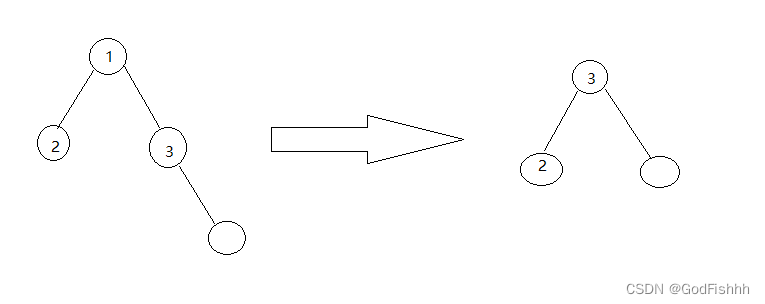
更简单地可以以如下的示意图表示:
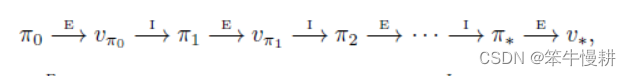
策略迭代与值迭代之间的关系【3】:
策略迭代中包含值迭代,策略评估是基于价值估计进行的,而价值估计是以值迭代的方式进行的。值迭代算法是策略评估过程只进行一次迭代的策略迭代算法。
3. 代码及仿真结果
3.1 class PolicyIterationPlanner()
estimate_by_policy()用于在当前策略下估计状态期望值,该状态期望值用于第(2)步中的基于价值的最佳行动选择。estimate_by_policy()与ValueIterationPlanner中的价值估计略有不同,这里是估计期望值(但是实际上由于是确定性策略,所以实际上也退化为当前策略下的最佳行动的价值),而后者是直接估计最佳行动的价值。
plan()实现了上一章所描述的流程。在迭代过程中将每次迭代后的价值估计结果打印出来,以方便结果的观测和理解。
print_policy()用于将最后得到的策略打印出来。
class PolicyIterationPlanner(Planner):
def __init__(self, env):
super().__init__(env)
self.policy = {}
def initialize(self):
super().initialize()
self.policy = {}
actions = self.env.actions
states = self.env.states
for s in states:
self.policy[s] = {}
for a in actions:
# Initialize policy.
# At first, each action is taken uniformly.
self.policy[s][a] = 1 / len(actions)
def estimate_by_policy(self, gamma, threshold):
V = {}
for s in self.env.states:
# Initialize each state's expected reward.
V[s] = 0
while True:
delta = 0
for s in V:
expected_rewards = []
for a in self.policy[s]:
action_prob = self.policy[s][a]
r = 0
for prob, next_state, reward in self.transitions_at(s, a):
r += action_prob * prob * \
(reward + gamma * V[next_state])
expected_rewards.append(r)
value = sum(expected_rewards)
delta = max(delta, abs(value - V[s]))
V[s] = value
if delta < threshold:
break
return V
def plan(self, gamma=0.9, threshold=0.0001):
self.initialize()
states = self.env.states
actions = self.env.actions
def take_max_action(action_value_dict):
return max(action_value_dict, key=action_value_dict.get)
while True:
update_stable = True
# Estimate expected rewards under current policy.
V = self.estimate_by_policy(gamma, threshold)
self.log.append(self.dict_to_grid(V))
for s in states:
# Get an action following to the current policy.
policy_action = take_max_action(self.policy[s])
# Compare with other actions.
action_rewards = {}
for a in actions:
r = 0
for prob, next_state, reward in self.transitions_at(s, a):
r += prob * (reward + gamma * V[next_state])
action_rewards[a] = r
best_action = take_max_action(action_rewards)
if policy_action != best_action:
update_stable = False
# Update policy (set best_action prob=1, otherwise=0 (greedy))
for a in self.policy[s]:
prob = 1 if a == best_action else 0
self.policy[s][a] = prob
# Turn dictionary to grid
self.V_grid = self.dict_to_grid(V)
self.iters = self.iters + 1
print('PolicyIteration: iters = {0}'.format(self.iters))
self.print_value_grid()
print('******************************')
if update_stable:
# If policy isn't updated, stop iteration
break
def print_policy(self):
print('PolicyIteration: policy = ')
actions = self.env.actions
states = self.env.states
for s in states:
print('\tstate = {}'.format(s))
for a in actions:
print('\t\taction = {0}, prob = {1}'.format(a,self.policy[s][a]))3.2 测试代码
测试代码如下(作为对比,对valueIterPlanner也有一些修改,将中间结果打印出来了以方便对比):
if __name__ == "__main__":
# Create grid environment
grid = [
[0, 0, 0, 1],
[0, 9, 0, -1],
[0, 0, 0, 0]
]
env1 = Environment(grid)
valueIterPlanner = ValueIterationPlanner(env1)
valueIterPlanner.plan(0.9,0.001)
valueIterPlanner.print_value_grid()
env2 = Environment(grid)
policyIterPlanner = PolicyIterationPlanner(env2)
policyIterPlanner.plan(0.9,0.001)
policyIterPlanner.print_value_grid()
policyIterPlanner.print_policy() 3.3 运行结果
3.3.1 价值估计结果
ValueIteration: iters = 1
-0.040 -0.040 0.792 0.000
-0.040 0.000 0.434 0.000
-0.040 -0.040 0.269 0.058
******************************
......
ValueIteration: iters = 10
0.610 0.766 0.928 0.000
0.487 0.000 0.585 0.000
0.374 0.327 0.428 0.189
******************************
PolicyIteration: iters = 1
-0.270 -0.141 0.102 0.000
-0.345 0.000 -0.487 0.000
-0.399 -0.455 -0.537 -0.728
******************************
......
PolicyIteration: iters = 4
0.610 0.766 0.928 0.000
0.487 0.000 0.585 0.000
0.374 0.327 0.428 0.189
******************************
价值迭代和策略迭代得到的最终价值估计结果是相同的。 但是策略迭代只用了4次迭代就收敛了,而价值迭代则用了10次迭代。
3.3.2 策略迭代得到的最终策略
策略迭代最终得到的策略结果如下所示:
PolicyIteration: policy =
state = <State: [0, 0]>
action = Action.UP, prob = 0
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 0
action = Action.RIGHT, prob = 1
state = <State: [0, 1]>
action = Action.UP, prob = 0
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 0
action = Action.RIGHT, prob = 1
state = <State: [0, 2]>
action = Action.UP, prob = 0
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 0
action = Action.RIGHT, prob = 1
state = <State: [0, 3]>
action = Action.UP, prob = 1
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 0
action = Action.RIGHT, prob = 0
state = <State: [1, 0]>
action = Action.UP, prob = 1
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 0
action = Action.RIGHT, prob = 0
state = <State: [1, 2]>
action = Action.UP, prob = 1
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 0
action = Action.RIGHT, prob = 0
state = <State: [1, 3]>
action = Action.UP, prob = 1
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 0
action = Action.RIGHT, prob = 0
state = <State: [2, 0]>
action = Action.UP, prob = 1
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 0
action = Action.RIGHT, prob = 0
state = <State: [2, 1]>
action = Action.UP, prob = 0
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 0
action = Action.RIGHT, prob = 1
state = <State: [2, 2]>
action = Action.UP, prob = 1
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 0
action = Action.RIGHT, prob = 0
state = <State: [2, 3]>
action = Action.UP, prob = 0
action = Action.DOWN, prob = 0
action = Action.LEFT, prob = 1
action = Action.RIGHT, prob = 0
这个结果可以图示化如下(【4】,忽略以上结果中在[0,3]和[1,3]的结果):
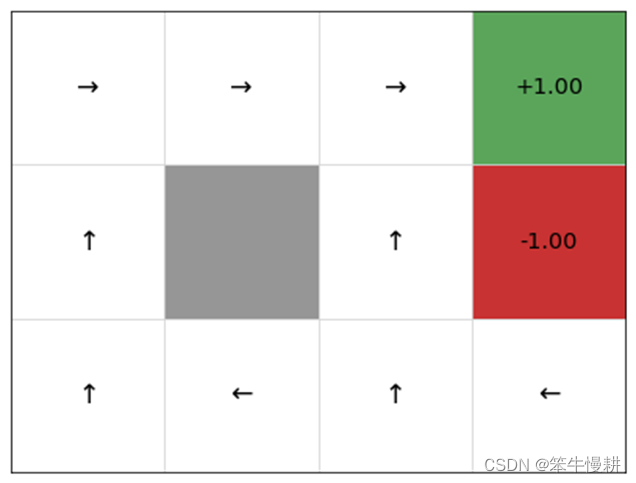
【思考】
以上策略迭代中的策略更新方式只能以greedy的方式进行吗?以greedy的方式进行策略更新,最后得到的策略也必然是确定性的策略,即在每个状态下,只有某一个最佳行动的概率为1,其余行动的概率为0。
强化学习笔记:强化学习笔记总目录
完整代码参见::reinforcement-learning/value_eval at main · chenxy3791/reinforcement-learning (github.com)
参考文献:
【1】Sutton, et, al, Introduction to reinforcement learning (2020)
【2】久保隆宏著,用Python动手学习强化学习
【3】策略迭代(Policy Iteration)和值迭代(Value Iteration) - 知乎 (zhihu.com)
【4】Policy iteration — Introduction to Reinforcement Learning (gibberblot.github.io)








![Java高效率复习-线程基础[线程]](https://img-blog.csdnimg.cn/cc96b79b2579424abc2e6ec1846ac666.png)