二叉树的构造和相关功能的代码实现及解析

news2024/9/22 3:47:38

目录

一.二叉树类的定义

二.构造二叉树（构造函数）

三.为二叉树插入节点(insert_value)

四.移除根节点(remove_root,lchild_leaf)

五.移除二叉树中的某值(remove,remove_value)

六.清空二叉树

七.前、中、后序遍历

一.二叉树类的定义

  二叉树类的定义需定义两个类，分别为BTnode来存放二叉树的相关信息(如节点的值，左子树、右子树的地址等)和BinaryTree来声明二叉树的相关操作。

C++代码：

//BinaryTree.h


#ifndef _BINARYTREE_H_
#define _BINARYTREE_H_

#pragma once

#include<iostream>
using namespace std;


template<typename valType>
class BTnode
{
	//使BTnode与BinaryTree类建立友谊关系，BinaryTree类可以直接使用BTnode类中的data member
	friend class BinaryTree<valType>;
private:
	valType _val;
	int _cnt;
	BTnode* _lchild;
	BTnode* _rchild;
public:
	BTnode() { _val = 0; _cnt = 0;_lchild=_rchild =0 };
	BTnode(const valType& val);
	~BTnode() { };
	void lchind_leaf(BTnode* leaf, BTnode* subtree); //remove操作中的某个特殊情况
	void remove_value(const valType& val, BTnode*& prev); //作为remove操作中的操作函数
};

template<typename elemType>
class BinaryTree
{
private:
	BTnode<elemType>* _root;
public:
	BinaryTree() { _root = 0 }; //默认构造函数
	BinaryTree(const BinaryTree&rhs);
	~BinrayTree(){} ;
	void remove(const elemType& elem); //移除某值
	void remove_root(); //移除根节点
	void clear(BTnode<elemType>*pt); //清空二叉树
	void insert_value(const elemType& val); //为二叉树插入节点

	//遍历：

    //前序
	void preorder(BTnode*pt,ostream& os)const;

	//中序
	void inorder(BTnode*pt,ostream& os)const;

	//后序
	void postorder(BTnode*pt,ostream& os)const;

	void display_val(BTnode*pt,ostream* os)const;
};




#endif

friend class BinaryTree<valType>;

在BTnode类中加入上述语句使BTnode类与BinaryTree类建立友谊关系，BinaryTree类可以直接使用BTnode类中的data member。

二.构造二叉树（构造函数）

  通过成员初始化完成data member _val的初始化（因为_val的类型是valType,如果valType是一个类，则可能无法通过简单的赋值运算通过初始化）。

  建议将所有的template类型参数当作为"class"类型来处理，因而将其声明为一个const reference而不是by value来传递。

C++代码：

template<typename valType>
BTnode<valType>::BTnode(const valType& val):_val(val)
{
	_cnt = 1;
	_lchild = _rchild = 0;
}

template<typename elemType>
BinaryTree<elemType>::BinaryTree(const BinaryTree& rhs):_root(rhs._root)
{

}

对于模板类，第一次出现需要声明为BTnode<valType>加以限定，第二次出现的BTnode已经被视为在class定义范围内，则把无需再加以限定

三.为二叉树插入节点(insert_value)

主要通过递归实现

节点插入的基本原理：左子树的值小于根节点，右子树的值大于根节点。通过递归直到找到某个根节点的左/右子树不存在，创建左/右子树并将val赋值给该节点。

C++代码：

template<typename elemType>
void BinaryTree<elemType>::insert_value(const elemType& val)
{
	if (val == _val)
	{
		_cnt++;
		return;
	}
	if (val < _val)
	{
		if (!_child) //如果此时该根节点的左子树不存在，则创造一个新的左子树用于存放新节点
		{
			_lchild = new BTnode(val);
		}
		//如果存在，则继续递归直到找到不存在的地方
		else
		{
			_lchild->insert_value(val);
		}
	}
	else
	{
		//对于右子树的操作相同
		if (!_rchild)
		{
			_rchild = new BTnode(val);
		}
		else
		{
			_rchild->insert_value(val);
		}
	}
}

四.移除根节点(remove_root,lchild_leaf)

原理：如果根节点拥有任何子节点，remove_root将重设根节点。如果右节点存在，则以右节点取而代之；如果右节点不存在而左节点存在，则root直接用左节点取代。

细节：当根节点的右节点存在时，用右节点取代该根节点，但此时左节点应当如何放置？有两种情况。

①.该右节点的左子节点存在:

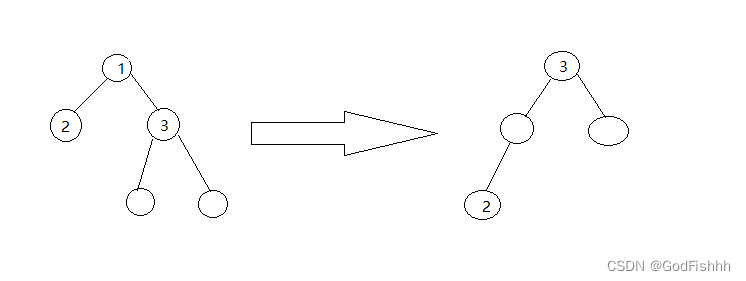         左节点接在右节点(即当前的根节点)的左子节点的左端。

②.该右节点的左子节点不存在

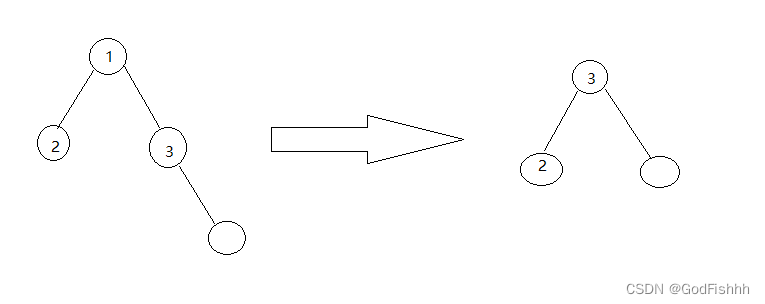
 左节点直接接在右节点(即当前根节点)的左子节点处。

C++代码：

template<typename valType>
void BTnode<valType>::lchind_leaf(BTnode* leaf, BTnode* subtree)
{
	while (subtree->_lchild) //如果subtree的左子节点存在，则一直向下递归直到某个subtree不存在 
左子节点再将leaf放在subtree的左子节点处
	{
		subtree = subtree->_lchild;
	}
	subtree->_lchild = leaf;
}


template<typename elemType>
void BinaryTree<elemType>::remove_root()
{
	if (!_root)
	{
		return;
	}

	//创建一个指针用来保存要删除的节点
	BTnode<elemType>* tmp = _root;
	if (_root->rchild) //如果右节点存在，则用右节点来替换根节点
	{
		_root = _root->_rchild;
	}

	if (tmp->_lchild) //如果根节点的左节点存在
	{
		BTnode<elemType>* lc = tmp->_lchild; //lc是是根节点的左节点
		BTnode<elemType>* newlc = _root->_lchild; //newlc是右节点的左节点
		if (!newlc) //如果右节点的左节点不存在
		{
			_root->_lchild = lc; //则直接将左节点放在此处
		}
		else
		{
			BTnode<elemType>::lchild)leaf(lc,newlc); //若右节点的左节点存在，则将根节点的左节点放在右节点的左子树的最底段的左节点处。
		}
	}
	else //右节点不存在 
	{
		_root = _root->lchild;
	}

	delete tmp;
}

五.移除二叉树中的某值(remove,remove_value)

原理：左子树的值小于根节点，右子树的值大于根节点，再通过递归一层一层的搜索下去。

C++代码：

template<typename valType>
void BTnode<valType>::remove_value(const valType& val, BTnode*& prev)
{
	if (val < _val) //则往左子树递归
	{
		if (!_child) //已经不存在左节点，即该二叉树中不存在该值
		{
			return;
		}
		else
		{
			_lchild->remove_value(val, _lchild);
		}
	}
	else if (val > _val) //则刚右子树递归
	{
		if (!_right)
		{
			retur;
		}
		else
		{
			_rchild->remove_value(val,_rchild)
		}
	}
	else //val = _val的情况，即找到该节点，接下来考虑remove操作的过程
	{
		if (_rchild)//如果右子树存在，则用右子树来替换根节点 (_rchild其实为this->rchild)
		{
			prev = _rchild;
			if (_lchild) //如果左子树存在，则需要进行下列操作来处理左子树
			{
				if (!prev->_lchild) //如果该右节点不存在左子节点，则直接将_lchild接在该位置
				{
					prev->_lchild = _lchild;
				}
				else
				{
					//右节点的左子节点存在，通过提前设定好的lchild_leaf函数将_lchild放在_rchild的左子节点的左端
					lchind_leaf(_lchild, prev->_lchild);
				}
			}
		}
		else //右子树不存在
		{
			prev = _lchild;
		}
		delete this; //删除节点
	}
}

template<typename elemType>
void BinaryTree<elemType>::remove(const elemType& elem)
{
	if (_root) //_root节点仍存在
	{
		if (_root->_val == elem) //如果此时节点的值已经等于参数elem,则直接删除该根节点
		{
			remove_root();
		}
		else //如果此时节点的值不等于参数elem，则通过remove_value函数递归找到该节点并删除
		{
			_root->remove_value(elem, _root);
		}
	}
}

void BTnode<valType>::remove_value(const valType& val, BTnode*& prev)

remove_value第二个参数是一个reference to pointer，因为我们既需要改变pointer所指之物，也要改变pointer本身。

①pointer作为参数:  改变pointer所指之物。

②reference作为参数:改变reference引用本身。

六.清空二叉树

原理：通过递归分左右两条路线进行delete操作来清空二叉树

C++代码：


template<typename elemType>
void BinaryTree<elemType>::clear(BTnode<elemType>*pt)
{
	if (pt)
	{
		clear(pt->_lchild);
		clear(pt->_rchild);
		delete pt;
	}
}

七.前、中、后序遍历

原理：以对根的访问顺序来作为分类点。

①.前序遍历：根节点 左节点 右节点

②.中序遍历：左节点 根节点 右节点

③.后序遍历：左节点 右节点 根节点

而访问根节点 左节点 右节点的代码实现如下：

根节点：

display_val(pt, os);

左节点：

if (pt->_lchild)
{
	preorder(pt->_lchild, os);
}

右节点：

if (pt->_rchild)
{
	preorder(pt->_rchild, os);
}

因此只需要对这三段代码进行排列组合，即可得到三种遍历方法。

C++代码：

//遍历：

//前序
template<typename valType>
void BTnode<valType>::preorder(BTnode* pt, ostream& os)const
{
	display_val(pt, os);
	if (pt->_lchild)
	{
		preorder(pt->_lchild, os);
	}
	if (pt->_rchild)
	{
		preorder(pt->_rchild, os);
	}
}

//中序
template<typename valType>
void BTnode<valType>::inorder(BTnode* pt, ostream& os)const
{
	if (pt->_lchild)
	{
		preorder(pt->_lchild, os);
	}
	display_val(pt, os);
	if (pt->_rchild)
	{
		preorder(pt->_rchild, os);
	}
}

//后序
template<typename valType>
void BTnode<valType>::postorder(BTnode* pt, ostream& os)const
{
	if (pt->_lchild)
	{
		preorder(pt->_lchild, os);
	}
	if (pt->_rchild)
	{
		preorder(pt->_rchild, os);
	}
	display_val(pt, os);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/182245.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Django入门学习-了解基本模块

Django入门学习-了解基本模块

目录 MVT设计了解 认识MVT 实际操作 Template&#xff1a; View: 路由配置 Model: 默认的后台管理模块 初始化admin模块 应用中Admin注册 MVT设计了解 认识MVT Django的web设计模型是MVT&#xff1a; Model&#xff1a;数据存储层&#xff0c;处理所有数据相关的业…
阅读更多...
idea+ApifoxUploader+Apifox真是内外双修，香

idea+ApifoxUploader+Apifox真是内外双修，香

前言 最近部门为整合后端组、前端组、测试组、需求组、产品组等组之间的工作流程&#xff0c;旨在提高协调与高效&#xff0c;其中之一就是希望开发组&#xff08;后端、前端&#xff09;开发的接口能及时更新&#xff0c;测试组能做接口测试&#xff0c;后期方便出文档&#x…
阅读更多...
大公司为什么禁止SpringBoot项目使用Tomcat？

大公司为什么禁止SpringBoot项目使用Tomcat？

本文已经收录到Github仓库&#xff0c;该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点&#xff0c;欢迎star~ Github地址&#xff1a;https://github.com/…
阅读更多...
【2】burpsuite屏蔽浏览器无用流量包方法

【2】burpsuite屏蔽浏览器无用流量包方法

0x01 问题描述经常会使用火狐或者谷歌去burpsuite对站点进行测试&#xff0c;但是在测试的过程中burpsuite经常抓到火狐浏览器自身的数据包或者其他无用的数据包&#xff0c;这就对我们工作的效率大有影响&#xff0c;所以这里来告诉大家如何解决此类问题。0x02 问题复现访问网…
阅读更多...
星环科技数据治理与数据价值评估实践分享

星环科技数据治理与数据价值评估实践分享

数据价值评估背景 自2015年8月国务院《促进大数据发展行动纲要》提出“数据已成为国家基础性战略资源”以来&#xff0c;我国出台了诸多政策和法案&#xff0c;推进数据的发展和数据要素的资产化。 2019年10月&#xff0c;第十九届四中全会关于《推进国家治理体系和治理能力现…
阅读更多...
Node.js安装详细教程

Node.js安装详细教程

安装 Node.js 官网下载安装包https://nodejs.org/zh-cn/&#xff0c;一直【下一步】安装即可。 设置Windows操作系统全局环境变量 为什么设置环境变量&#xff1f; 当我们在cmd命令行中输入命令时&#xff0c;系统首先会在当前目录下去找命令对应的可执行程序&#xff0c;如果…
阅读更多...
后端校验（hibernate-validator）

后端校验（hibernate-validator）

目录一、介绍和依赖二、方法的 Model 参数校验三、方法的非 Model 参数校验四、常用注解五、快速失败六、自定义校验规则一、介绍和依赖 hibernate-validator 是 Java 中常用的后端校验框架 https://docs.jboss.org/hibernate/stable/validator/reference/en-US/html_single/【…
阅读更多...
提取各种数据结构中的元素将提取结果合并为迭代对象 itertools.chain(*a,b)

提取各种数据结构中的元素将提取结果合并为迭代对象 itertools.chain(*a,b)

【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 提取各种数据结构中的元素 将提取结果合并为迭代对象 itertools.chain(*a,b) [太阳]选择题 以下python代码最后输出正确的一项是? from itertools import chain a[(1, A), (2, B), …
阅读更多...
Java高效率复习-线程基础[线程]

Java高效率复习-线程基础[线程]

内容大纲 线程相关概念 并发并行 当只有一个CPU时&#xff0c;会执行并发的效果&#xff0c;在多个应用程序之间快速切换&#xff0c;而有多个CPU时&#xff0c;则多个CPU独立执行&#xff0c;而当进程多于CPU个数时&#xff0c;则会出现并发并行的情况&#xff0c;总有一个CPU…
阅读更多...
如何炼就数据分析的思维？

如何炼就数据分析的思维？

目录 前言结构化思维假说演绎思维指标化思维维度分析思维 前言 面对数据异常&#xff0c;我们经常会出现“好像是A原因引起的&#xff1f;”“貌似和B原因也相关&#xff1f;““有可能是 C操作不当“的主观臆测。 或者&#xff0c;拿到一个分析议题&#xff0c;分析”11 月销售…
阅读更多...
@ConfigurationProperties注解使用方法（内含源代码）

@ConfigurationProperties注解使用方法（内含源代码）

ConfigurationProperties注解使用方法&#xff08;内含源代码&#xff09; 源代码下载链接地址&#xff1a;https://download.csdn.net/download/weixin_46411355/87400774 目录ConfigurationProperties注解使用方法&#xff08;内含源代码&#xff09;源代码下载链接地址&…
阅读更多...
怎么识别截图中的文字？这三个方法让你轻松学会

怎么识别截图中的文字？这三个方法让你轻松学会

在日常工作或学习中&#xff0c;我们会经常在网上查阅一些资料&#xff0c;当遇到一些优美的句子或者段落时&#xff0c;都会手动摘抄下来&#xff0c;这种记录方式不仅很耗时&#xff0c;还耗费精力&#xff0c;并且现在很多网站都已经不支持文本复制了&#xff0c;遇到这种情…
阅读更多...
6.验证面试高频问题整理(附答案)

6.验证面试高频问题整理(附答案)

目录 Q126.top-down phase、bottom-up phase有哪些 Q127.为什么build_phase是top-down phase&#xff0c;connect_phase是bottom-up phase Q128.$size用于packed array和unpacked array分别得到的什么 Q129.class和struct的异同 Q130.class和module的异同 Q131.对象创建的…
阅读更多...
MAC系统 LightGBM模型转为pmml格式

MAC系统 LightGBM模型转为pmml格式

一、配置JAVA环境和Maven环境 参考以下两个博客即可 MAC 系统安装 JDK 及环境变量配置_蜗牛的博客-CSDN博客_mac jdk环境变量配置 MAC 系统安装 Maven 及环境变量配置_蜗牛的博客-CSDN博客_mac安装mpv 二、下载JPMML-LightGBM 先在Git上下载 直接下载或使用git clone http…
阅读更多...
Aop切面编程原理和Spring实现

Aop切面编程原理和Spring实现

Aop切面编程概念 AOP切面编程一般可以帮助我们在不修改现有代码的情况下,对程序的功能进行拓展,往往用于实现 日志处理,权限控制,性能检测,事务控制等 AOP实现的原理就是动态代理,在有接口的情况下,使用JDK动态代理,在没有接口的情况下使用cglib动态代理 为Dao层所有的add方法…
阅读更多...
字体反爬，一种来自字体设计师的跨行反爬案例 | 案例 28

字体反爬，一种来自字体设计师的跨行反爬案例 | 案例 28

本篇博客涉及的内容非常有价值&#xff0c;尤其是在反爬领域。 核心内容为自定义字体文件反爬。 文章目录准备工作在 Web 页面中使用字体文件整理文字编码Flask 中随机一串数字&#xff0c;渲染到前台总结准备工作 在正式编写代码前&#xff0c;需要先安装 FontCreator &#…
阅读更多...
GeoServer学习笔记-01GeoSever运行编译

GeoServer学习笔记-01GeoSever运行编译

一、运行1. 下载GeoServerGitHub仓库地址&#xff1a;https://github.com/geoserver/geoserver2.本地代码工具打开项目在idea里&#xff0c;文件->新建->来自现有的源代码项目&#xff0c;选择项目的pom文件加载项目。3.idea编译环境设置&#xff08;1&#xff09;设置jd…
阅读更多...
图论（5）最小生成树简单应用

图论（5）最小生成树简单应用

活动 - AcWing 参考&#xff1a;《算法竞赛进阶指南》-lyd 目录 一、基础算法 二、 1.最短网络&#xff08;prim板子&#xff09; 2.局域网&#xff08;kruskal板子&#xff09; 3.繁忙的都市 4.1143. 联络员 5.连接格点&#xff08;预处理&#xff09; 一、基础算法…
阅读更多...
影响电商发展的重要因素及电商未来的发展可能

影响电商发展的重要因素及电商未来的发展可能

易观分析&#xff1a;自从互联网传入中国以后&#xff0c;特别是2000年以后&#xff0c;一直保持着非常快的演变速度&#xff0c;而以互联网为基础的电商则更是发展成了中国互联网的代表性行业。中国电商的发展不仅在初期有着非常高的增速&#xff0c;有着多样化的演进路线&…
阅读更多...
Numpy(3)—切片和索引、高级索引、Broadcast、迭代数组、广播迭代

Numpy(3)—切片和索引、高级索引、Broadcast、迭代数组、广播迭代

1.切片和索引 eg1&#xff1a;我们首先通过 arange() 函数创建 ndarray对象。 然后&#xff0c;分别设置起始&#xff0c;终止和步长的参数为 2&#xff0c;7 和 2。 import numpy as npa np.arange(10) s slice(2, 7, 2) # 从索引 2 开始到索引 7 停止&#xff0c;间隔为…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023