CST Studio Suite 基础操作实验（稳恒电流的电场与磁场）

news2024/11/24 6:41:06

前言

前置的基础操作可见笔者之前一篇文章，在此不再赘述

因为整个实验要求都要用英文，有些不便更改部分的英文就没翻译了，见谅

CST Studio Suite 基础操作实验（静电场）-CSDN博客

核心步骤

  • 无限长设置

假如是z轴上的无限长设置，那么只需要对background进行如下修改即可，将z的distance设置为零，由于镜像，其长度在z轴上即为无限长

  • 模型建造

可以直接通过参数设置以满足具体实验要求

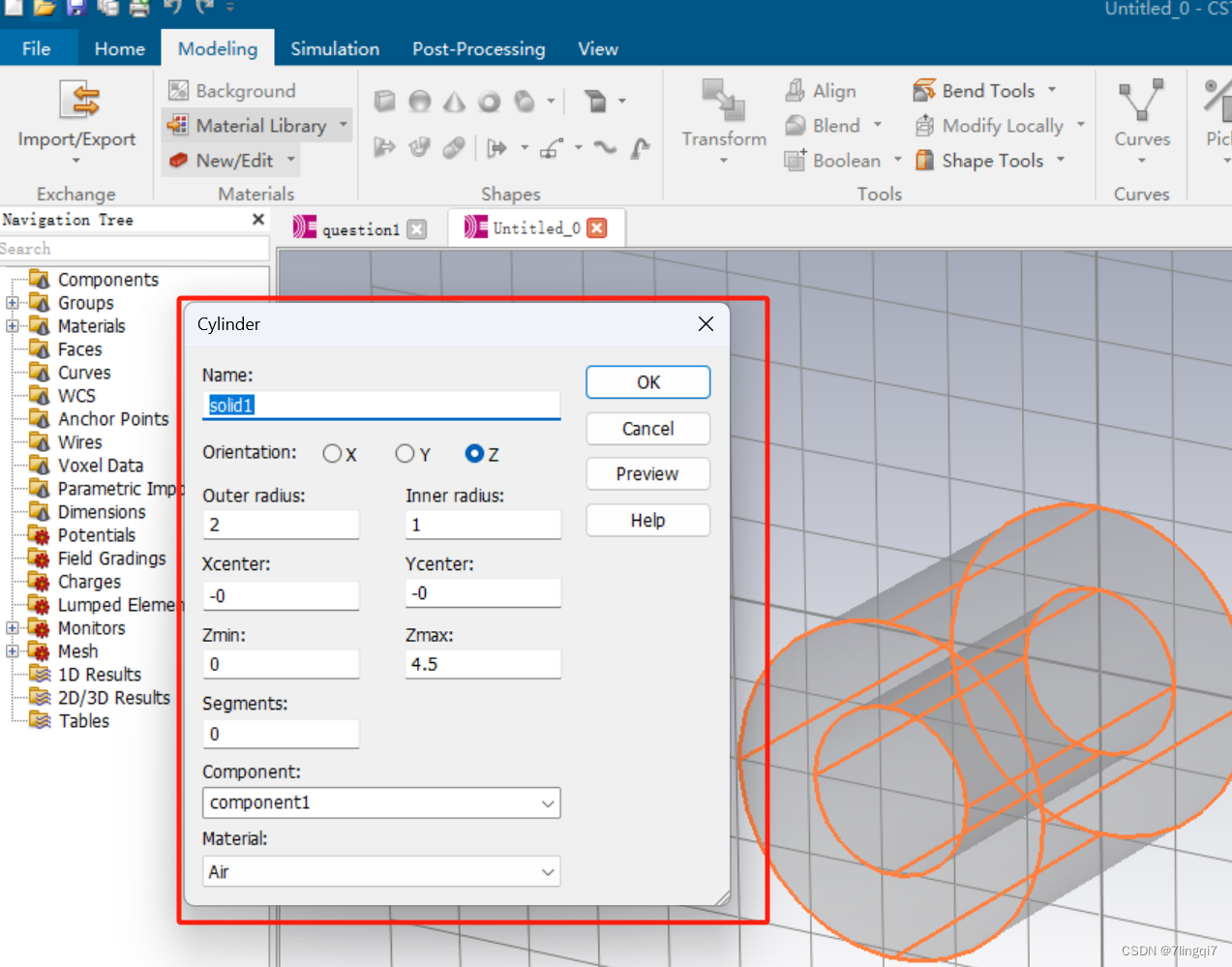
  • Solver选择

再做下一步之前一定要先选定好solver，不然很多界面操作都不一样

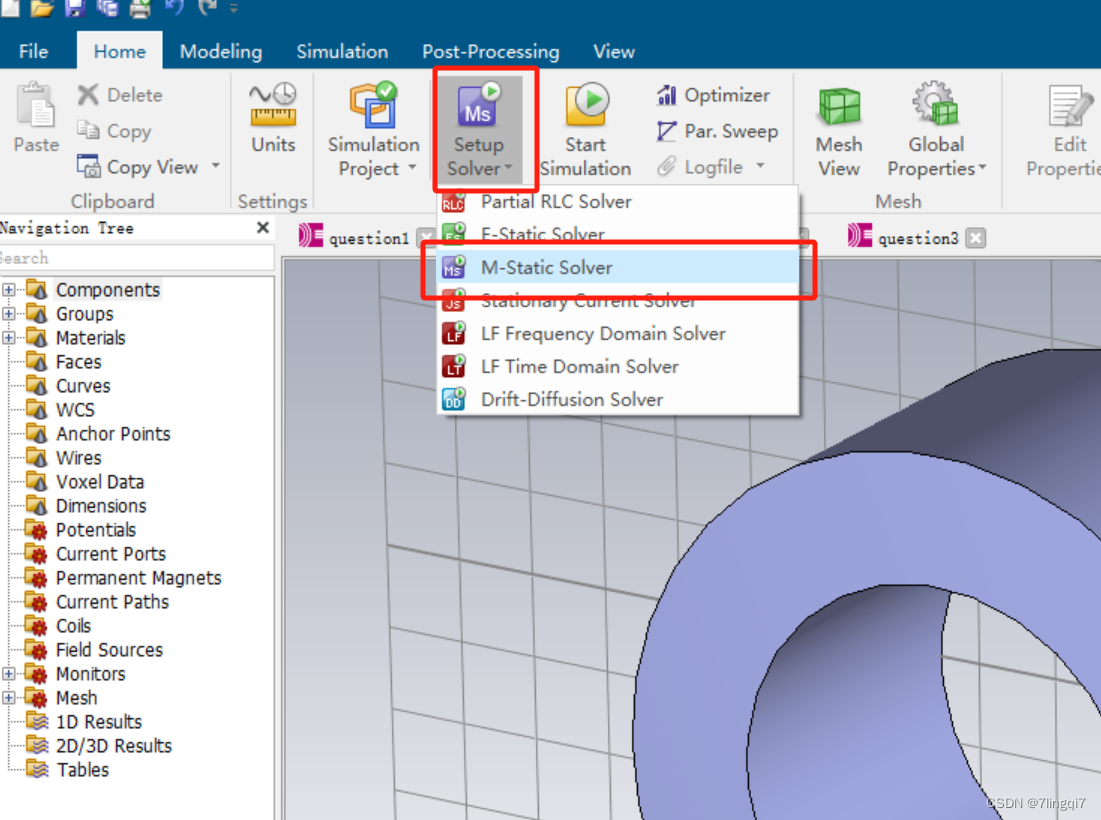
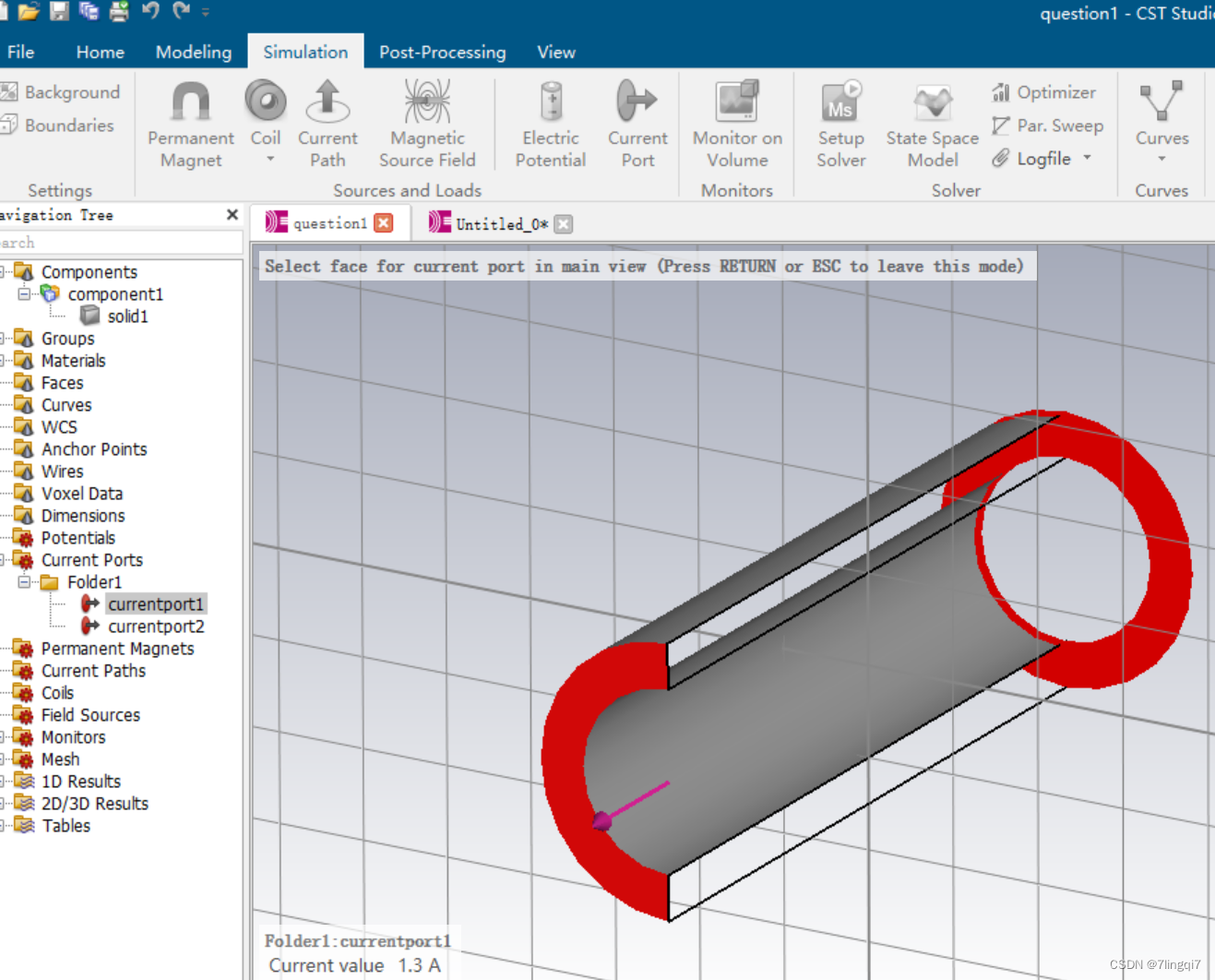
  • 轴向电流设定

按照下图进行电流设置，但要注意同轴电流朝向一定要相同，倘若不相同则勾选Invert current direction进行方向的调转，两个面都要设置电流

朝屏幕内的面不是很好设置，可以使用modeling的cutting plane去查看切开的视图再去设置

第一题

仿真模型：

无限长空心圆柱轴线为z轴，内外半径分别为1mm和1.5mm，其上均匀分布轴向电流(1+0.3)A，求x轴上B的大小。

材料选用normal，步骤略

理论问题：

内外半径分别为a和b的无限长空心圆柱中均匀分布轴向电流I，求柱内外的磁感应强度。

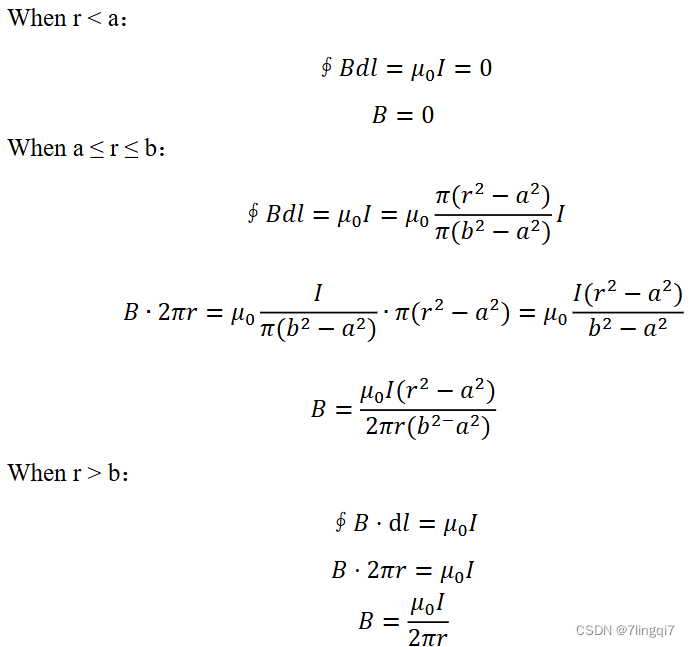
matlab代码

% Constants
mu_0 = 4 * pi * 1e-7; % Permeability of free space (H/m)
I_base = 1; % Base current (A)
adj = 3/10; % Given adjustment factor
I_total = I_base * (1 + adj); % Total current (A)

% Radii of the cylinder
r_inner = 1e-3; % Inner radius (m)
r_outer = 1.5e-3; % Outer radius (m)

% Define x positions where B is to be calculated
x_positions = linspace(0, 10e-3, 100); % Example x positions from 0 to 10mm

% Initialize B array
B = zeros(size(x_positions));

% Calculate B at each x position
for i = 1:length(x_positions)
    x = x_positions(i);
    if abs(x) <= r_inner
        % Inside the inner radius, B is 0
        B(i) = 0;
    elseif abs(x) > r_inner && abs(x) <= r_outer
        % Between inner and outer radius
        B(i) = (mu_0 * I_total / (2 * pi * abs(x))) * (abs(x)^2 - r_inner^2) / (r_outer^2 - r_inner^2);
    else
        % Outside the outer radius
        B(i) = (mu_0 * I_total / (2 * pi * abs(x))) * (r_outer^2 - r_inner^2) / (r_outer^2 - r_inner^2);
    end
end

% Load data from file
data_B = importdata('B1.txt');
if isstruct(data_B)
    data_B = data_B.data;
end

% Extract X values and B-Field values
x_exp_B = data_B(:, 1); % First column
B_exp = data_B(:, 2); % Second column

% Plot B vs x
figure;
plot(x_positions * 1e3, B, 'LineWidth', 2, 'DisplayName', 'Calculated B-Field'); % Convert x_positions to mm for plotting
hold on;
plot(x_exp_B, B_exp, 'r--', 'LineWidth', 2, 'Marker', 'o', 'MarkerSize', 3, 'DisplayName', 'Experimental B-Field');
xlabel('Position (x) [mm]');
ylabel('Magnetic Field (B) [T]');
title('Magnetic Field (B) along the x-axis');
xlim([0, 10]); % Correct usage of xlim
grid on;
legend('show');

结果分析和比较

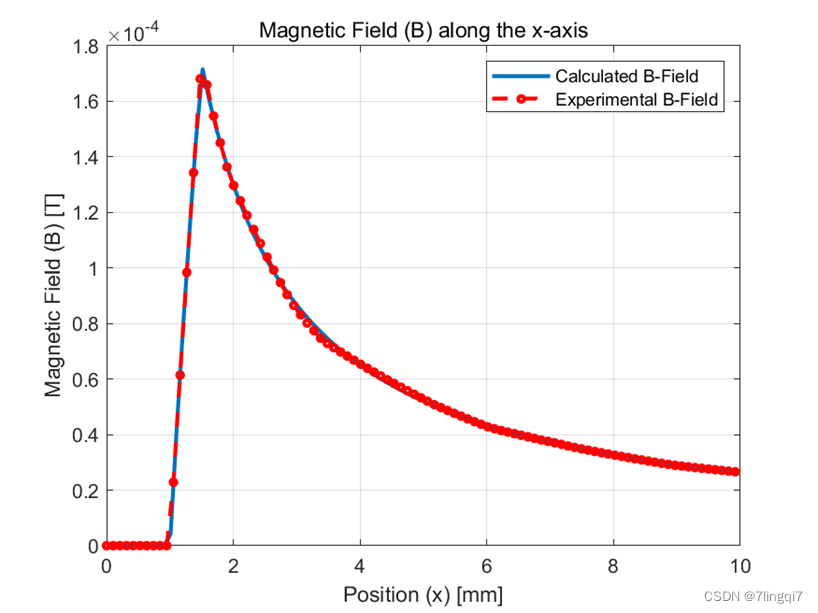
我们首先分析计算值和模拟值的 B 分布趋势。从图中我们可以看出，B 分布是对称的，因此我们只分析沿正 x 轴的 B 分布。当 0<=x<1.5mm 时，B 分布等于 0；当 1.5<=x<2 时，B 分布呈线性增长。当 x>=2mm 时，B 分布按反比例函数递减。
当 0 <= x <= 2mm 时，计算值与模拟值一致。当 x > 2mm 时，所有部分重合。

第二题

仿真模型：

载流的圆形导线半径为(20+0.3)mm,求圆心处B的大小。电流为1A

按照下图绘制圆形导线

理论问题：

同轴线内外导体半径为a，外导体的内半径为b,外半径为c，如下图。设内外导体分别流过反相的电流，两导体之间介质的磁导率为μ,求各区域的H、B。若电流流向+z方向

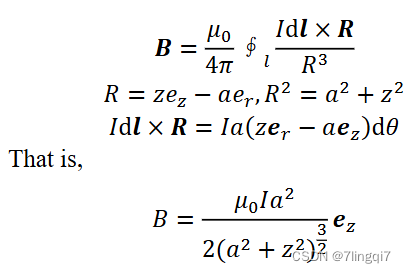
matlab代码

% Constants
mu_0 = 4 * pi * 1e-7; % Permeability of free space (H/m)
I_total = 1; % Total current (A)

adj = 3 / 10; % Given adjustment factor
% Radius of the circular wire
radius = (20 + adj) * 1e-3; % Radius in meters

% Define x positions where B is to be calculated
x_positions = linspace(-10e-3, 10e-3, 100); % Example x positions from -10 to 10mm

% Calculate B at each x position
B = mu_0 * I_total * radius^2 ./ (2 * (radius^2 + x_positions.^2).^(3/2));

% Load data from file
data_B = importdata("B2.txt");
if isstruct(data_B)
    data_B = data_B.data;
end

% Extract X values and B-Field values
x_exp_B = data_B(:, 1); % First column
B_exp = data_B(:, 2); % Second column

% Plot B vs x
figure;
plot(x_positions * 1e3, B, 'LineWidth', 2, 'DisplayName', 'Calculated B-Field'); % Convert x_positions to mm for plotting
hold on;
plot(x_exp_B, B_exp, 'r--', 'LineWidth', 2, 'Marker', 'o', 'MarkerSize', 3, 'DisplayName', 'Experimental B-Field');
xlabel('Position (x) [mm]');
ylabel('Magnetic Field (B) [T]');
title('Magnetic Field (B) along the x-axis');
xlim([-10, 10]); % Correct usage of xlim
grid on;
legend('show');

结果分析和比较

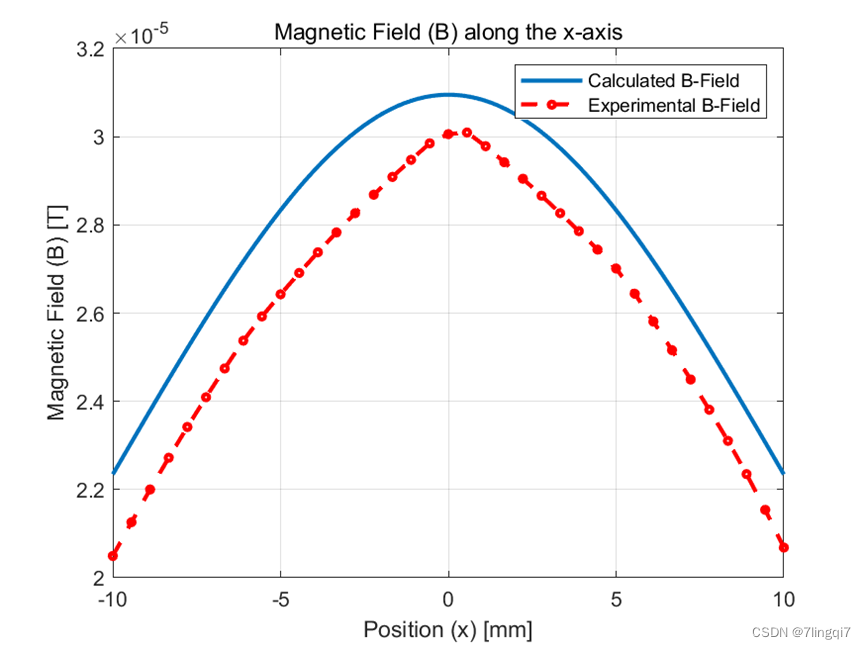
我们首先分析计算值和模拟值的 B 分布趋势。从图中可以看出，B 分布是对称的，因此我们只分析沿正 x 轴的 B 分布。当 x = 0mm 时，B 分布达到最大值。当 x > 0mm 时，B 分布按反比例函数递减。
我们注意到计算值与模拟值有一定的偏差。
这两种差异可能是边界条件造成的，也可能是求解器精度造成的。在实验中，我设置的边界条件等于 30，这与实际情况相比相对较小。虽然存在微小误差，但这是可以接受的，因为不可能绝对模拟真实情况。

第三题

仿真模型：

同轴线轴线为z轴，a=0.5mm,b=1mm,c=1.5mm, 两导体之间介质的相对磁导率为(4+0.3)，求x轴上的H、B。（记得上反向的电）

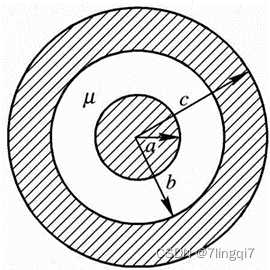
建造一个三个同心圆柱即可，在参数设置的时候设定实验要求的大小

理论问题：

求载流的圆形导线回路在圆心处的B。

matlab代码

% Constants
mu_0 = 4 * pi * 1e-7; % Permeability of free space (H/m)
adj = 3/10; % Given adj
mu_r = 4 + adj; % Relative permeability
I_current = 1; % Current (A)

% Radii
radius_inner = 0.5e-3; % Inner radius (m)
radius_middle = 1e-3; % Middle radius (m)
radius_outer = 1.5e-3; % Outer radius (m)

% Define x positions where H and B are to be calculated
x_positions = linspace(0, 5e-3, 100); % Example x positions from 0 to 5mm

% Initialize H and B arrays
H_field = zeros(size(x_positions));
B_flux = zeros(size(x_positions));

% Calculate H and B at each x position
for i = 1:length(x_positions)
    x_pos = x_positions(i);
    if abs(x_pos) < radius_inner
        % Region 1: r < a
        H_field(i) = I_current * abs(x_pos) / (2 * pi * radius_inner^2);
        B_flux(i) = mu_0 * H_field(i);
    elseif abs(x_pos) >= radius_inner && abs(x_pos) < radius_middle
        % Region 2: a <= r < b
        H_field(i) = I_current / (2 * pi * abs(x_pos));
        B_flux(i) = mu_0 * mu_r * H_field(i);
    elseif abs(x_pos) >= radius_middle && abs(x_pos) < radius_outer
        % Region 3: b <= r < c
        H_field(i) = (I_current / (2 * pi * abs(x_pos))) - (I_current * (abs(x_pos) - radius_middle) / (2 * pi * radius_outer^2));
        B_flux(i) = mu_0 * H_field(i);
    else
        % Region 4: r >= c
        H_field(i) = 0;
        B_flux(i) = 0;
    end
end

% Load data from file
data_H = importdata('H3.txt');
if isstruct(data_H)
    data_H = data_H.data;
end

% Load data from file
data_B = importdata('B3.txt');
if isstruct(data_B)
    data_B = data_B.data;
end


% Extract X values and H-Field values
x_exp_H = data_H(:, 1); % First column
H_exp = data_H(:, 2); % Second column

% Extract X values and B-Field values
x_exp_B = data_B(:, 1); % First column
B_exp = data_B(:, 2); % Second column

% Plot H and B vs x
figure;
subplot(2, 1, 1);
plot(x_positions * 1e3, H_field, 'LineWidth', 2, 'DisplayName', 'Calculated H-Field'); % Convert x_positions to mm for plotting
hold on;
plot(x_exp_H, H_exp, 'r--', 'LineWidth', 2, 'Marker', 'o', 'MarkerSize', 3, 'DisplayName', 'Experimental H-Field');
xlabel('Position (x) [mm]');
ylabel('Magnetic field H (A/m)');
title('Magnetic field H along the x-axis');
grid on;
legend('show');

subplot(2, 1, 2);
plot(x_positions * 1e3, B_flux, 'LineWidth', 2, 'DisplayName', 'Calculated B-Field'); % Convert x_positions to mm for plotting
hold on;
plot(x_exp_B, B_exp, 'r--', 'LineWidth', 2, 'Marker', 'o', 'MarkerSize', 3, 'DisplayName', 'Experimental B-Field');
xlabel('Position (x) [mm]');
ylabel('Magnetic flux density B (T)');
title('Magnetic flux density B along the x-axis');
grid on;
legend('show');

结果分析和比较

我们首先分析计算值和模拟值的 B 分布和 H 分布的趋势。从图中可以看出，B 分布和 H 分布是对称的，因此我们只分析沿正 x 轴的 B 分布和 H 分布。当 x = 0mm 时，B 分布等于 0。当 x = 0.5mm 时，B 分布达到最大值。当 0.5 < x < 1mm 时，B 分布按反比例函数递减。当 1 < x < 1.5mm 时，B 分布呈线性递减。当 x >= 1.5mm 时，B 分布等于 0。当 x = 0mm 时，H 分布等于 0。当 0 < x < 0.5mm 时，H 分布按反比例函数递减。当 0.5 <= x < 1.5mm 时，H 分布呈线性递减趋势。当 x >= 1.5mm 时，H 分布等于 0。
磁场强度 H 的比较：计算结果和实验结果在内侧和中间半径显示出相同的趋势，但在外侧半径有一些偏差。这可能是由于简化模型未能捕捉到实验中复杂的边界条件和材料特性变化。

磁通密度 B 的比较：同样，计算结果和实验结果在内半径和中间半径处显示出相同的趋势，但在外半径处的数值存在一些偏差。这可能与实验设备、材料特性或模型简化的误差有关。

第四题

仿真模型：

如下图所示，两个圆柱半径为1mm, 轴线与z轴平行，轴线位置分别为x=0.5mm和x=-0.5mm, 除两柱重叠部分R外，两柱上各有大小相等、方向相反的电流1A, 求x轴上[-0.4mm,0.4mm]范围上B的大小。

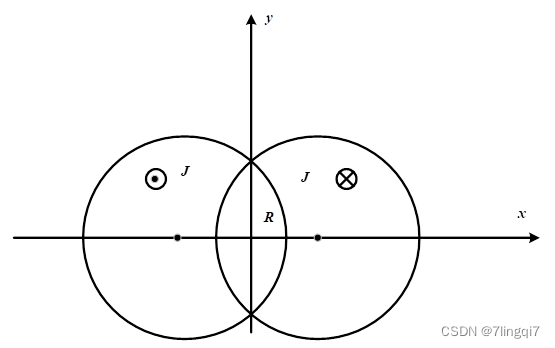
这个模型需要灵活运用下面的操作调整到如下图所示的图形

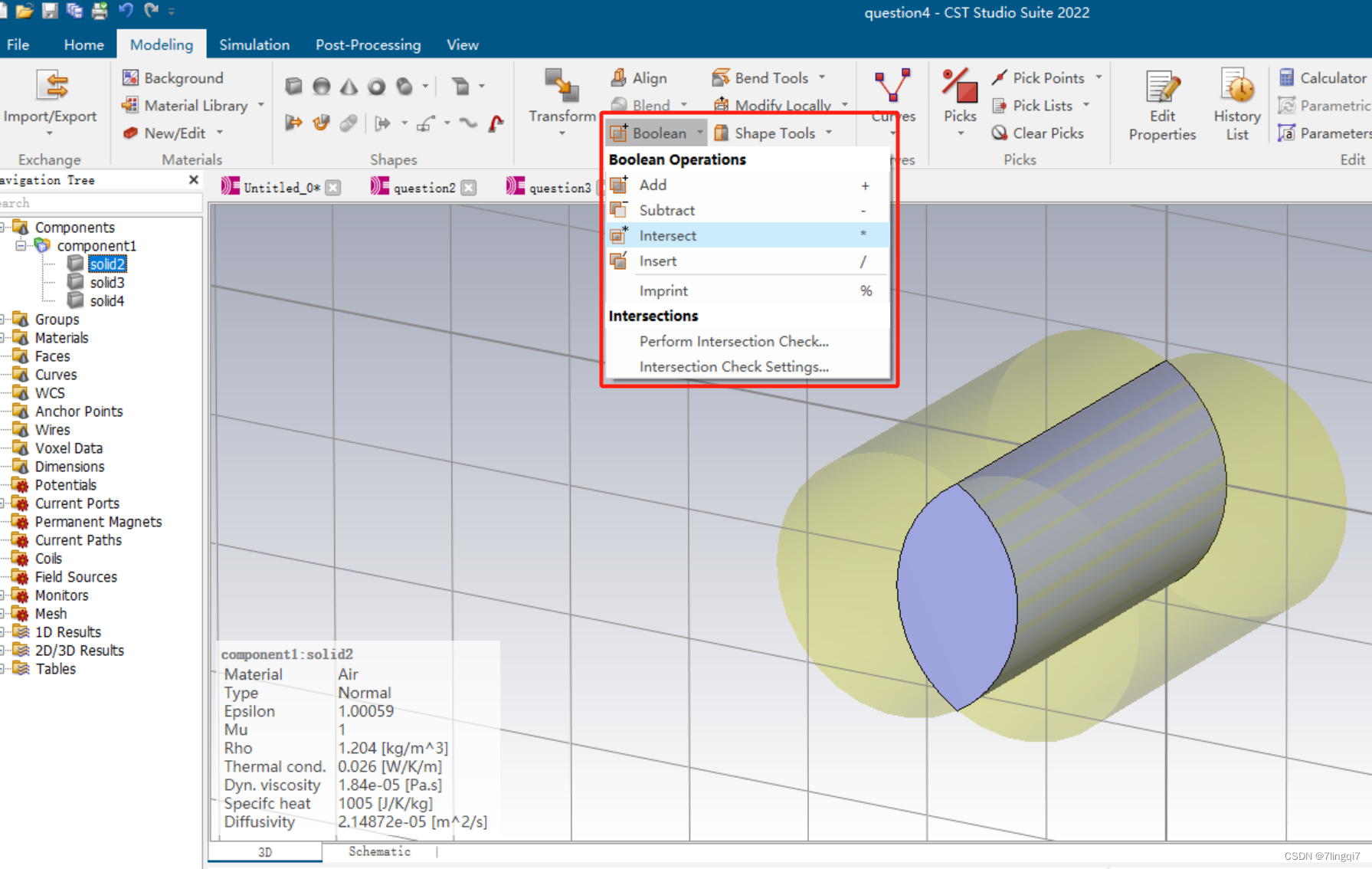
理论问题：

两个半径都为a的圆柱体，轴间距为d, d<2a，如下图。除两柱重叠部分R外，两柱上各有大小相等、方向相反的电流，密度为J,求区域R的B。

matlab代码

% Constants definition
mu_0 = 4 * pi * 10^-7; % Vacuum permeability in H/m
radius = 0.001; % Radius in meters
distance = 0.001; % Distance between axes in meters
I_current = 1; % Current in Amperes

% Calculate current density
J_density = I_current / ((1/3) * pi * radius^2 + (sqrt(3)/2) * radius^2); % Current density in A/m^2

% Define x-axis range
x_positions = -0.0005:0.00001:0.0005; % x-axis from -0.5mm to 0.5mm

% Calculate magnetic field B
B_field = (mu_0 * J_density * distance) / 2 * ones(size(x_positions)); % B is constant in this range

% Load data from file
data_B = importdata("B4.txt").data;

% Calculate the mean of the imported data
mean_data_B = mean(data_B(:, 2));

% Plot the results
figure;
plot(x_positions * 1000, B_field, 'LineWidth', 2, 'DisplayName', 'Calculated'); % Convert x to mm for better readability
hold on;
plot(data_B(:, 1), data_B(:, 2), '--o', 'LineWidth', 2, 'MarkerSize', 3, 'DisplayName', 'Imported');
xlabel('x (mm)');
ylabel('B (T)');
ylim([min(min(B_field), min(data_B(:, 2))) * 0.5, max(max(B_field), max(data_B(:, 2))) * 1.5]); % Adjust y-axis limits
title('Magnetic Field B along x-axis');
grid on;
legend('show');

结果分析和比较

我们首先分析了计算值和模拟值的 B 分布趋势。在[-0.4,0.4]毫米范围内，B 分布是一个常数，即在此范围内 B 分布值相同。
从图中可以看出，计算值与模拟值基本吻合，这说明我们的实验设置是合理的。
 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1821556.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

《分析模式》第2章中文UML图（已修正原书错误）（2.1-2.6）

《分析模式》第2章中文UML图（已修正原书错误）（2.1-2.6）

DDD领域驱动设计批评文集 做强化自测题获得“软件方法建模师”称号 《软件方法》各章合集 &#xff08;1&#xff09;已用UML、OCL表示&#xff0c;并翻译为中文。 &#xff08;2&#xff09;已修正原书图存在的错误&#xff08;多重性、角色&#xff09;&#xff0c;之前的…
阅读更多...
前端必看的2024 年 7 个 Web 前端开发趋势【文末福利=网盘分享2024web前端技术资料，学习资源】

前端必看的2024 年 7 个 Web 前端开发趋势【文末福利=网盘分享2024web前端技术资料，学习资源】

目录 前言 趋势一&#xff1a;新的样式解决方案和组件库将持续涌现 趋势二&#xff1a;利用 AI 来增强开发流程 趋势三&#xff1a;SSR 和 SSG 两种框架之间的竞争将会愈演愈烈 趋势四&#xff1a;前端、后端和全栈开发之间的界限将越来越模糊 趋势五&#xff1a;越来越多的人…
阅读更多...
江协科技51单片机学习- p5 LED灯闪烁

江协科技51单片机学习- p5 LED灯闪烁

前言&#xff1a; 本文是根据哔哩哔哩网站上“江协科技51单片机”视频的学习笔记&#xff0c;在这里会记录下江协科技51单片机开发板的配套视频教程所作的实验和学习笔记内容。本文大量引用了江协科技51单片机教学视频和链接中的内容。 引用&#xff1a; 51单片机入门教程-2…
阅读更多...
轻兔推荐 —— Obsidian

轻兔推荐 —— Obsidian

via&#xff1a;轻兔推荐 - https://app.lighttools.net/ 简介 Obsidian 是一个强大的知识管理和笔记应用程序&#xff0c;它基于本地文件存储&#xff0c;支持Markdown格式&#xff0c;并提供丰富的插件生态系统。 - 通过双向链接和图谱视图&#xff0c;帮助用户发现笔记之间…
阅读更多...
掌握midjourney系列：8 个角色设计关键词

掌握midjourney系列：8 个角色设计关键词

Midjourney V6的角色引用功能非常强大&#xff0c;可以让多张图片生成的角色风格保持一致。在实现同一角色的多张场景图片之前&#xff0c;我们需要先设计好基础角色。 以下是我总结的Midjourney中人物设计套路的常用提示&#xff0c;很高兴与大家分享。 1、角色设定表&#…
阅读更多...
杏仁核亚区在情绪处理中的特化

杏仁核亚区在情绪处理中的特化

摘要 杏仁核对人类的恐惧情绪处理至关重要。然而&#xff0c;目前的研究未能揭示其特异性&#xff0c;有证据表明杏仁核也会对其他情绪做出反应。鉴于情绪功能对日常生活和心理健康的重要性&#xff0c;我们需要更加细致地了解杏仁核在情绪加工中的作用&#xff0c;特别是与恐…
阅读更多...
短剧系统源码短剧平台开发短剧小程序APP短剧模版Java源码

短剧系统源码短剧平台开发短剧小程序APP短剧模版Java源码

一.管理端设置及操作 1.系统配置 系统的配置项都在该列表中,使用前请配置好参数 2.签到积分设置 签到可以获取设置积分,连续签到按照设置的积分规则走,积分可以兑换余额,兑换比例按照配置104,余额可以消费 3.用户中心 所有的用户注册后都会在该列表展示,可以查看用户详情,也…
阅读更多...
Spring-事件

Spring-事件

Java 事件/监听器编程模型 设计模式-观察者模式的拓展 可观察者对象(消息发送者) Java.util.Observalbe观察者 java.util.Observer 标准化接口(标记接口) 事件对象 java.util.EventObject事件监听器 java.util.EventListener public class ObserverDemo {public static vo…
阅读更多...
神经网络 torch.nn---nn.LSTM()

神经网络 torch.nn---nn.LSTM()

torch.nn - PyTorch中文文档 (pytorch-cn.readthedocs.io) LSTM — PyTorch 2.3 documentation LSTM层的作用 LSTM层:长短时记忆网络层&#xff0c;它的主要作用是对输入序列进行处理&#xff0c;对序列中的每个元素进行编码并保存它们的状态&#xff0c;以便后续的处理。 …
阅读更多...
H5的3D展示有可能代替PC传统3D展示么？

H5的3D展示有可能代替PC传统3D展示么？

H5的3D展示技术正在快速发展&#xff0c;并且随着5G网络的普及和手机硬件性能的提升&#xff0c;H5的3D展示在某些方面已经能够接近甚至超越传统PC上的3D展示效果&#xff0c;比如 博维数孪 的渲染能力及效果。但H5和PC的3D展示互相之间是各有优势领域和行业支持&#xff0c;短…
阅读更多...
hw面试总结

hw面试总结

在这里给大家推荐一个阿里云的活动&#xff0c;可白嫖一年2h4g服务器 活动链接&#xff1a;https://university.aliyun.com/mobile?clubTaskBizsubTask…11404246…10212…&userCodeks0bglxp 一、漏洞分析 1.SQL注入 原理&#xff1a; 当Web应用向后台数据库传递SQL…
阅读更多...
LLM之RAG实战（四十）| 使用LangChain SQL Agent和MySQL搭建多层RAG ChatBot

LLM之RAG实战（四十）| 使用LangChain SQL Agent和MySQL搭建多层RAG ChatBot

在传统的意义上&#xff0c;RAG 主要是从文档中检索用户想要的数据&#xff0c;从而提高大模型的能力&#xff0c;减少幻觉问题。今天&#xff0c;我们从另一个维度介绍RAG&#xff0c;RAG不从文档中获取数据&#xff0c;而是从MySQL数据库检索数据。我们可以使用LangChain SQL…
阅读更多...
Nature子刊：你的健康在出生就被肠道病毒定义了？

Nature子刊：你的健康在出生就被肠道病毒定义了？

近期&#xff0c;四川大学最新在《Nature Communications》期刊上(IF16.6)发表的“A metagenomic catalog of the early-life human gut virome”研究论文中&#xff0c;通过对宏病毒组结果进行分析&#xff0c;提供了最全面和最完整的生命早期人类肠道病毒组蓝图。 期刊&#…
阅读更多...
[图解]《分析模式》漫谈03-Party是什么

[图解]《分析模式》漫谈03-Party是什么

1 00:00:00,790 --> 00:00:03,930 今天我们来看一下&#xff0c;Party是什么 2 00:00:05,710 --> 00:00:07,470 当然我们这里说的不是政治的 3 00:00:07,880 --> 00:00:08,350 Party 4 00:00:09,230 --> 00:00:11,110 是《分析模式》里面的一个用词 5 00:00:14…
阅读更多...
短信群发平台选择时要看好对方的资质等问题！

短信群发平台选择时要看好对方的资质等问题！

在数字化营销日益盛行的今天&#xff0c;短信群发平台已成为企业与用户沟通的重要桥梁。然而&#xff0c;选择一个合适的短信群发平台并非易事&#xff0c;尤其需要考虑对方的资质等关键问题。 首先&#xff0c;资质是衡量一个短信群发平台是否正规、专业的重要指标。在选择平…
阅读更多...
美团的 AI 面试有点简单

美团的 AI 面试有点简单

刷到一个美团的 AI 实习生的面试帖子&#xff0c;帖子虽然不长&#xff0c;但是把美团 AI 评测算法实习生面试的问题都po出来了。 单纯的看帖子中面试官提出的问题&#xff0c;并不是很难&#xff0c;大部分集中在考察AI项目和对AI模型的理解上&#xff0c;并没有过多的考察AI算…
阅读更多...
企业服务器上云还是下云哪种比较好？-尚云Sunclouds

企业服务器上云还是下云哪种比较好？-尚云Sunclouds

如今很多中小企业都面临一个艰难的选择&#xff0c;是要选择将服务器迁移至数据中心托管&#xff08;下云&#xff09;或者直接迁移到云端&#xff08;上云&#xff09;。中小企业是社会发展的中坚力量&#xff0c;他们的特点少而明显&#xff1a;资金少&#xff0c;增长快&…
阅读更多...
【GTD时间管理法】“让‘聪明的自己“为“不太聪明的自己”打点好一切！

【GTD时间管理法】“让‘聪明的自己“为“不太聪明的自己”打点好一切！

大脑是用来思考而不是用来记事的。 该如何解放大脑&#xff0c;让我们能够有条不紊地处理好一切事情呢&#xff1f; 世界知名时间管理大师戴维艾伦认为&#xff0c;只需要三个步骤&#xff1a;清空大脑——制订计划——行动起来。他把这种时间管理方法称作“GTD”&#xff0c…
阅读更多...
【投稿优惠|权威主办】2024年能源、智能制造与材料科学国际学术会议（ICEIMMS 2024）

【投稿优惠|权威主办】2024年能源、智能制造与材料科学国际学术会议（ICEIMMS 2024）

【投稿优惠|权威主办】2024年能源、智能制造与材料科学国际学术会议&#xff08;ICEIMMS 2024&#xff09; 2024 International Academic Conference on Energy, Intelligent Manufacturing, and Materials Science&#xff08;ICEIMMS 2024&#xff09; ▶会议简介 2024年能源…
阅读更多...
净化机应用领域广泛 美国是我国净化机主要出口国

净化机应用领域广泛 美国是我国净化机主要出口国

净化机应用领域广泛 美国是我国净化机主要出口国 净化机&#xff0c;又称为空气清洁设备或空气清新机&#xff0c;是一种专门设计用于滤除或杀灭空气污染物、提升空气清洁度的装置。净化机具备高效的过滤功能&#xff0c;能够滤除空气中的悬浮微粒、细菌、病毒和花粉等污染物&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023