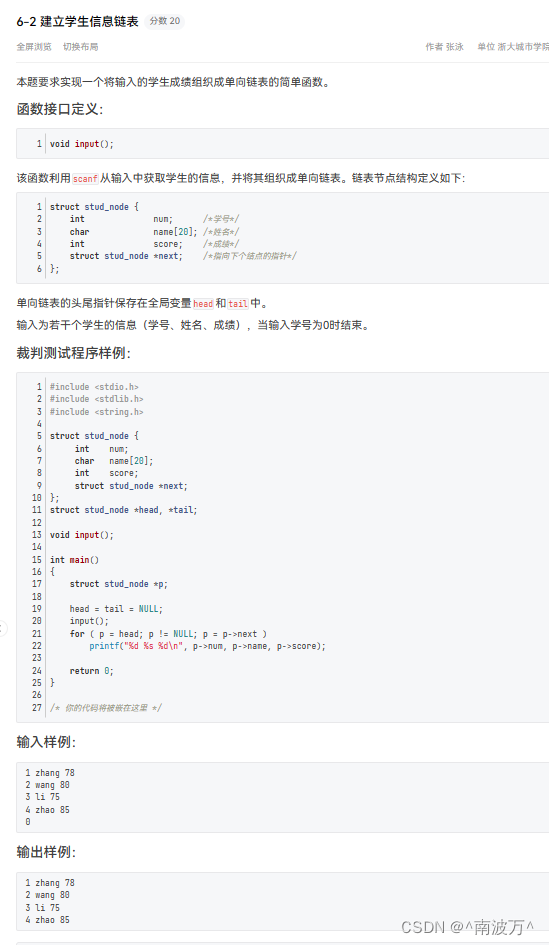
本节均以二分类问题为例进行展开,统一定义类别标签
y
∈
{
+
1
,
−
1
}
y\in\{+1,-1\}
y∈{+1,−1},则分类正确时
y
f
(
x
;
w
)
>
0
yf(x;w)>0
yf(x;w)>0,且值越大越正确;错误时
y
f
(
x
;
w
)
<
0
yf(x;w)<0
yf(x;w)<0,且值越小越错误。不同损失函数间的损失随
y
f
(
x
;
w
)
yf(x;w)
yf(x;w)变化如下图所示:
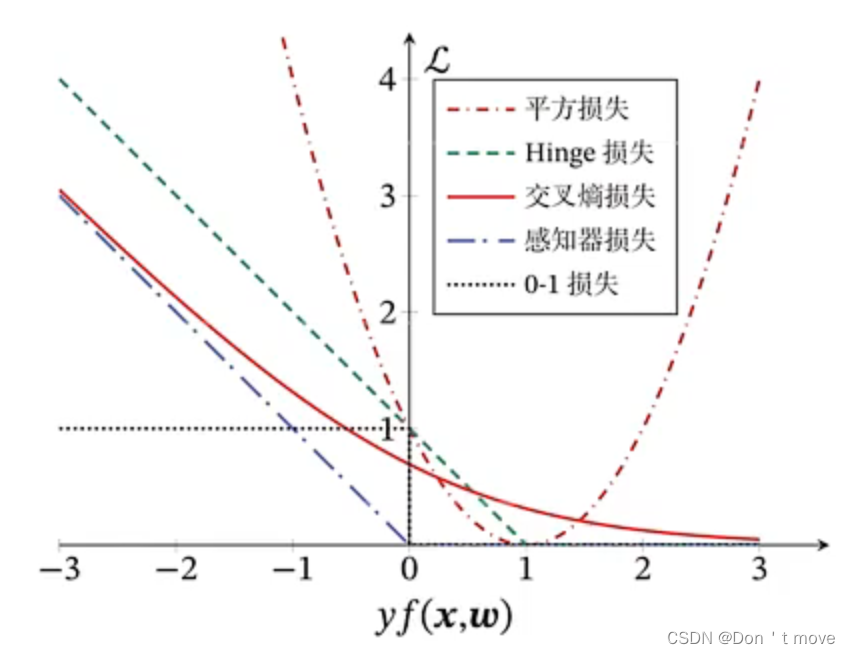
平方损失
L
=
(
y
−
f
(
x
;
w
)
)
2
=
y
2
−
2
y
f
(
x
;
w
)
+
f
2
(
x
;
w
)
=
1
−
2
y
f
(
x
;
w
)
+
y
2
f
2
(
x
;
w
)
=
(
1
−
y
f
(
x
;
w
)
)
2
\begin{aligned} \mathcal{L} &=(y-f(x;w))^2 \\ &=y^2-2yf(x;w)+f^2(x;w) \\ &=1-2yf(x;w)+y^2f^2(x;w) \\ &=(1-yf(x;w))^2 \end{aligned}
L=(y−f(x;w))2=y2−2yf(x;w)+f2(x;w)=1−2yf(x;w)+y2f2(x;w)=(1−yf(x;w))2
对于平方损失来说,当
y
f
(
x
;
w
)
<
1
yf(x;w)<1
yf(x;w)<1时,损失函数单调递减,此时如果用梯度下降进行优化,最终会收敛于点1。但当
y
f
(
x
;
w
)
>
1
yf(x;w)>1
yf(x;w)>1时,损失函数单调递减,同样在进行优化时还是会收敛于1,但事实上
y
f
(
x
;
w
)
yf(x;w)
yf(x;w)越大说明分类越正确。因此可以说,平方损失不适合做分类任务。
Logistic回归的损失函数(交叉熵损失)
L
=
−
I
(
y
=
1
)
log
σ
(
f
(
x
;
w
)
)
−
I
(
y
=
−
1
)
log
(
1
−
σ
(
f
(
x
;
w
)
)
)
=
−
I
(
y
=
1
)
log
σ
(
f
(
x
;
w
)
)
−
I
(
y
=
−
1
)
log
(
σ
(
−
f
(
x
;
w
)
)
)
=
−
log
σ
(
y
f
(
x
;
w
)
)
=
log
σ
−
1
(
y
f
(
x
;
w
)
)
=
log
(
1
+
exp
(
−
y
f
(
x
;
w
)
)
)
\begin{aligned} \mathcal{L} &=-I(y=1)\log\sigma(f(x;w))-I(y=-1)\log(1-\sigma(f(x;w)))\\ &=-I(y=1)\log\sigma(f(x;w))-I(y=-1)\log(\sigma(-f(x;w)))\\ &=-\log\sigma(yf(x;w))\\ &=\log\sigma^{-1}(yf(x;w))\\ &=\log(1+\exp(-yf(x;w))) \end{aligned}
L=−I(y=1)logσ(f(x;w))−I(y=−1)log(1−σ(f(x;w)))=−I(y=1)logσ(f(x;w))−I(y=−1)log(σ(−f(x;w)))=−logσ(yf(x;w))=logσ−1(yf(x;w))=log(1+exp(−yf(x;w)))
对于函数
σ
(
x
)
\sigma(x)
σ(x),可证
1
−
σ
(
x
)
=
σ
(
−
x
)
1-\sigma(x)=\sigma(-x)
1−σ(x)=σ(−x),且
I
I
I是指示函数,
I
(
y
=
1
)
=
1
y
=
1
=
{
1
y
=
1
0
y
=
−
1
I(y=1)=\mathbb{1}_{y=1}=\left\{\begin{aligned} &1&y=1\\\\ &0&y=-1 \end{aligned}\right.
I(y=1)=1y=1=⎩
⎨
⎧10y=1y=−1
I
(
y
=
−
1
)
=
1
y
=
−
1
=
{
1
y
=
−
1
0
y
=
1
I(y=-1)=\mathbb{1}_{y=-1}=\left\{\begin{aligned} &1&y=-1\\\\ &0&y=1 \end{aligned}\right.
I(y=−1)=1y=−1=⎩
⎨
⎧10y=−1y=1
由图像可知,随着
y
f
(
x
;
w
)
yf(x;w)
yf(x;w)的增大,函数损失逐渐减小最终趋于0。这样虽然满足了
y
f
(
x
;
w
)
yf(x;w)
yf(x;w)越大分类效果越好的条件,但其实这是没必要的,因为当损失大于0时就可以完成分类任务。因此虽然说交叉熵损失可以满足分类要求,但造成了一些不必要的计算,仍然具有改进空间。
感知器的损失函数
L
=
max
(
0
,
−
y
f
(
x
;
w
)
)
\mathcal{L}=\max(0,-yf(x;w))
L=max(0,−yf(x;w))
感知器损失解决了交叉熵损失的问题。感知器损失是专门为分类而设计的损失函数,其结果与真实效果基本一致。
软间隔支持向量机的损失函数(Hinge损失)
L
=
max
(
0
,
1
−
y
f
(
x
;
w
)
)
\mathcal{L}=\max(0,1-yf(x;w))
L=max(0,1−yf(x;w))
Hinge损失与感知器损失在几何上的不同仅仅在于Hinge损失在感知器损失的基础上向右平移了一个单位,这就导致了Hinge损失对距离分界面较近的样本(
y
f
(
x
;
w
)
yf(x;w)
yf(x;w)落在0到1之间)造成一定的惩罚。
结论
从模型健壮性角度来讲,选择支持向量机(Hinge损失)来解决一般分类问题的效果更好
各线性分类模型对比如下表所示

XOR问题
感知器和支持向量机虽然在线性可分问题上表现良好,但其无法解决非线性可分问题,例如XOR(异或)问题。
假设空间中有两个变量
(
x
1
,
x
2
)
(x_1,x_2)
(x1,x2),对两个变量分别取与、或、异或逻辑运算,结果如下图所示。

对于与运算和或运算产生的结果来说,总能找到一个分界面来把两类分开,也就是说这两个结果产生的数据集是线性可分的;但异或运算的结果无法直接找到一个分界面,也就是说它的结果数据是非线性可分的。XOR这类非线性可分问题是无法通过线性分类器来解决的。
要解决这类问题,可以借助使用”基函数“的广义线性模型,也就是把线性模型过一个基函数,让线性模型变为非线性的,也就是将
f
(
x
)
=
w
T
x
f(x)=w^Tx
f(x)=wTx变成
f
(
ϕ
(
x
)
)
=
w
T
ϕ
(
x
)
f(\phi(x))=w^T\phi(x)
f(ϕ(x))=wTϕ(x),这样就实现了将非线性可分的数据集映射到另一个空间中,映射的数据集在这个空间中是线性可分的。
以下图为例,
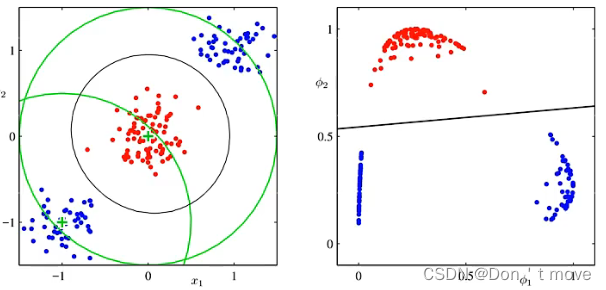
左图表示原来的数据集,可见该数据集是非线性可分的。但它有一个很明显的特征,对于这个数据集来说,可以找到一个中心点,计算样本到中心点的距离,使得中心点某个范围内的为一类,范围外的为另一类,这样就可以构建出一个特征函数,将原本非线性可分的数据集映射到线性可分的数据集上。(上面这个图是按照坐标(-1,-1)附近那个绿色中心点建立的,得到的结果就如右图所示)





![[数据集][目标检测]减速带检测数据集VOC+YOLO格式5400张1类别](https://img-blog.csdnimg.cn/direct/13f3fafa5a0740a392d2c0c3e4302e11.png)


![Siemens-NXUG二次开发-创建平面(无界非关联)、固定基准面[Python UF][20240614]](https://img-blog.csdnimg.cn/direct/cde449a65bd54e3385ef54f1aaa9169b.png#pic_center)