GNN和GCN的入门公式
- 一、GNN的计算
- 二、GCN的计算
跟随B站课程【GNN图神经网络最牛教程】学不会up直接下跪!图神经网络快速入门教程(GNN/GCN)的笔记
一、GNN的计算

对于一个图来说,要更新它自身的特征,也要更新它邻接节点的特征
m i = G ( { W j h j } : j ∈ N i ) m_{i}=G(\{W_{j}h_{j}\}: j \in N_{i}) mi=G({Wjhj}:j∈Ni)
其中 W j W_{j} Wj表示节点间的权重, h j h_{j} hj表示节点的特征值
总的更新公式就是
h i = σ ( W 1 h i + ∑ j ∈ N i W j h j ) h_{i}=\sigma(W_{1}h_{i}+\sum_{j\in N_{i}} W_{j}h_{j}) hi=σ(W1hi+j∈Ni∑Wjhj)
其中后半部分的求和部分还可以根据需求进行替换

二、GCN的计算

一个图计算的时候需要节点特征,邻接矩阵以及度矩阵。
因为邻接矩阵还要考虑自身节点,所以带上对角线变为1(就是节点自己和自己相连,一起引入计算)
A ~ = A + λ I N \tilde A=A+\lambda I_{N} A~=A+λIN

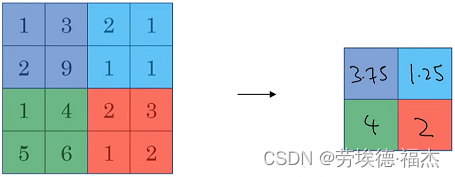
其中度矩阵是用来做归一化scale的(或者说求平均),这时候就需要用度来分化自身的权重。
D ~ − 1 A ~ \tilde D^{-1} \tilde A D~−1A~

D
~
−
1
A
~
X
\tilde D^{-1} \tilde AX
D~−1A~X

然后再乘特征矩阵X,但是这只是对行向量进行了平均,还要考虑对列向量平均
D ~ − 1 A ~ D ~ − 1 X \tilde D^{-1} \tilde A \tilde D^{-1} X D~−1A~D~−1X
但是这等于对行列进行了两次归一化,所以最终的形式是
A ^ = D ~ − 1 2 A ~ D ~ − 1 2 X \hat A= \tilde D^{-\frac{1}{2}} \tilde A \tilde D^{-\frac{1}{2}} X A^=D~−21A~D~−21X
整个两层神经网络的计算公式就是
Z = f ( X , A ) = s o f t m a x ( A ^ R e L U ( A ^ X W ( 0 ) ) W ( 1 ) ) Z=f(X, A)=softmax(\hat A ReLU(\hat AXW^{(0)})W^{(1)}) Z=f(X,A)=softmax(A^ReLU(A^XW(0))W(1))
然后GNN的层数一般比较少,一般两三层比较合适。