一,本文重点
- 线性最优化(LP)和标准线性最优化(Standard LP form)的定义
- 如何将LP转换为Standard LP
- 用Python解决LP问题
- 将非线性最优化问题(NLP)转换为LP
二,定义
1,线性最优化
- 定义
线性最优化问题,或者线性规划(linear programming,缩写:LP)是一个目标函数和所有限制函数(在决策变量中)都是线性的最优化问题。
注意:线性最优化是连续最优化的子集
- 普遍表达
一个LP问题通常可以写成如下模式:

m1,m2,m3是{1,...,m}的子集,n1,n2,n3是{1,...,n}的子集。
注意:最大化问题与之类似。
- 紧凑型表达
借助矩阵的知识,让形式更紧凑

在这里A1,A2,A3都是矩阵(维度为m1xn,m2xn,m3xn),b,d,e都是向量,变量x是维度为n的列向量。
2,标准形式(Standard LP form)
- 定义
标准型通常更系统和紧凑,在不同的课本中对标准形式的定义可能不同,在本系列采用如下形式。

x∈Rn,A是维度为m×n的矩阵,
三,将LP转换为Standard LP
1,说明
标准形式主要用于分析,平时解决问题只需要能够便于理解就行,但LP到Standard LP的转换技巧可以帮助我们分析和解决问题
2,技巧和步骤
(1)步骤
- 首先检查变量范围,Standard LP要求变量非负。
- 然后检查目标函数,将求最大转换为求最小
- 最后检查限制条件,将不等式转换为等式
(2)技巧(数学表达)
- maxx c⊤x → minx −c⊤x
- Ax ≤b →Ax+s =b,s ≥0
- Ax ≥b →Ax−s =b,s ≥0
- xi ≤ 0 →yi =−xi ≥0 free
- xi → xi = x+ i −x− i ,x+ i ≥ 0,x− i ≥ 0
3,示例
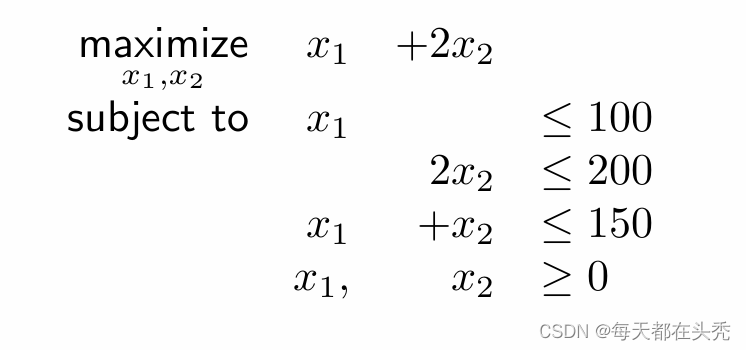
转化为standard LP:
minimize -x1 -2x2
s.t x1 +s1 =100
2x2 +s2 =200
x1 + x2 +s3 =150
x1, x2, s1, s2, s3 >=0
四,用Python解决LP问题
1,方案
被用来解决最优化问题的语言有MATLAB,Python,Julia,而一个非常重要的库是CVX。课上教授用的多是MATLAB,不过笨人更习惯Python,所以会用Python来解决课程中的问题。学习步骤如下:
- 下载cvxpy(Python中的CVX)
- 学习如何使用
- 解决问题
2,示例
以前文的例子为例:
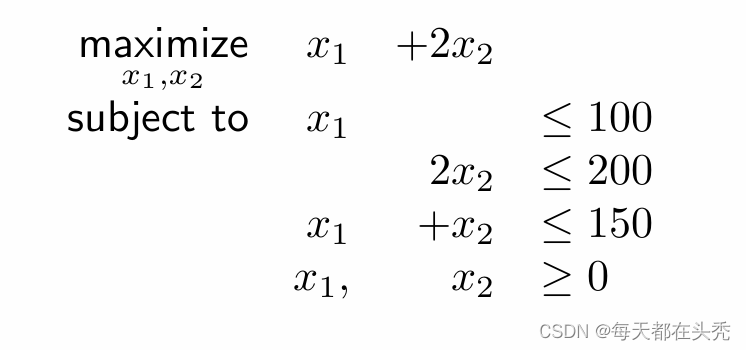
使用Python解决:
#import package
import cvxpy as cp
#decision variable
x1=cp.Variable()
x2=cp.Variable()
#constraint
consts=[x1<=100,2*x2<=200,x1+x2<=150,x1>=0,x2>=0]
#construct problem
obj=cp.Maximize(x1+2*x2)
prob=cp.Problem(obj,consts)
#output result
result=prob.solve()
x1_sol=x1.value
x2_sol=x2.value
print("Best result:",result)
print("Best x1:",x1_sol)
print("Best x2:",x2_sol)
'''
Output:
Best result: 249.99999997999043
Best x1: 49.99999998623639
Best x2: 99.99999999687702
'''五,非线性问题向线性问题的转化。
1,常见的非线性因素
- 目标函数或限制条件自带最大值最小值函数
- 目标函数或限制条件包含绝对值函数
对于两种问题有不同的解决方案
2,对于自带最大值最小值的问题
- 最大化问题
(1)思路
假设变量S小于或等于问题中的min
(2)示例:
原问题:

转换:
结果:
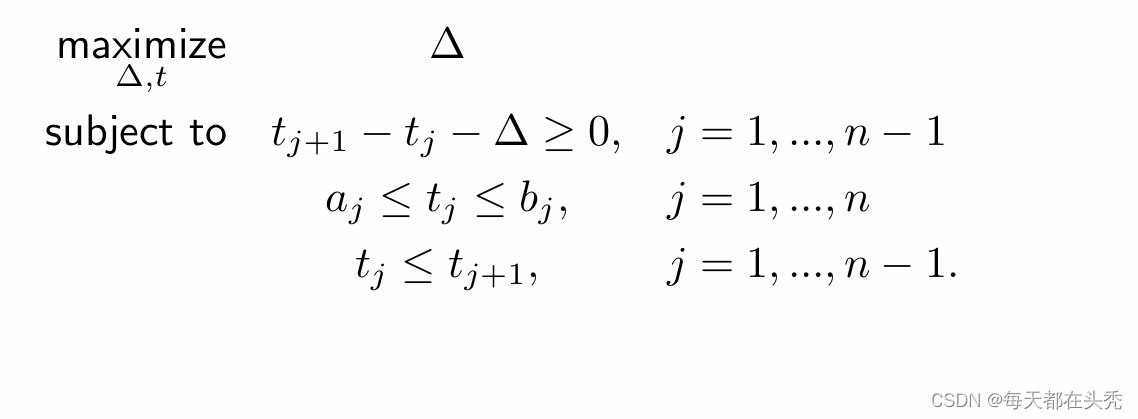
- 最小化问题
(1)思路
假设变量S大于或等于问题中的max
(2)示例
原问题:

转换:

结果:
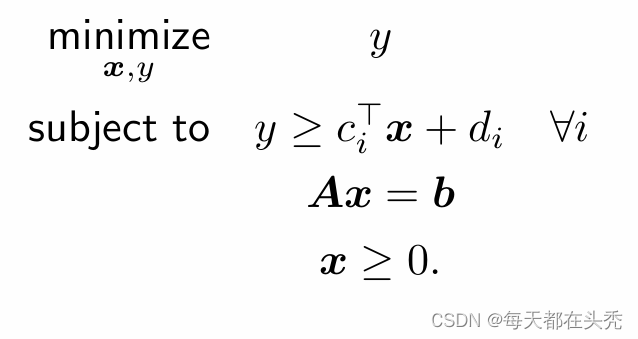
3,对于绝对值
- 最小化问题
采用最大值方式,假设变量t,使t大于或等于绝对值。
- 通用模式(可将绝对值扩展到函数)
假设变量t,使t大于或等于函数。
- 数学表达范例
可以转换成