文章目录
- 离散数学与组合数学-07命题逻辑
- 7.1 命题逻辑-什么是命题
- 7.1.1 数理逻辑发展
- 7.1.2 什么是命题
- 7.1.3 复合命题
- 7.2 命题逻辑-命题联结词
- 7.2.1 否定联结词
- 7.2.2 合取联结词
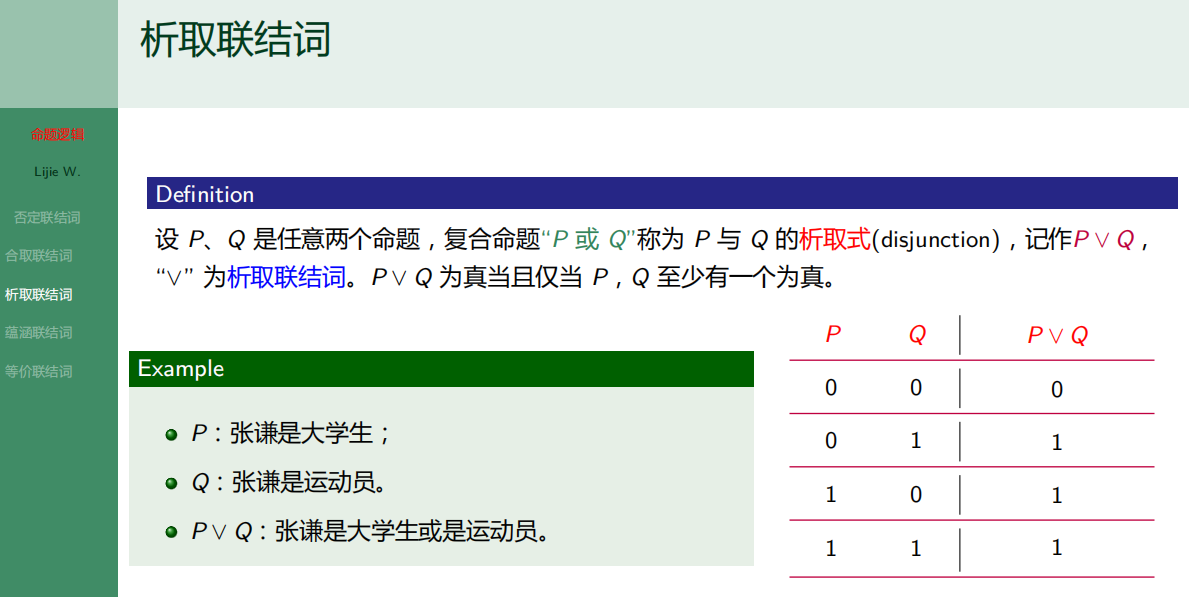
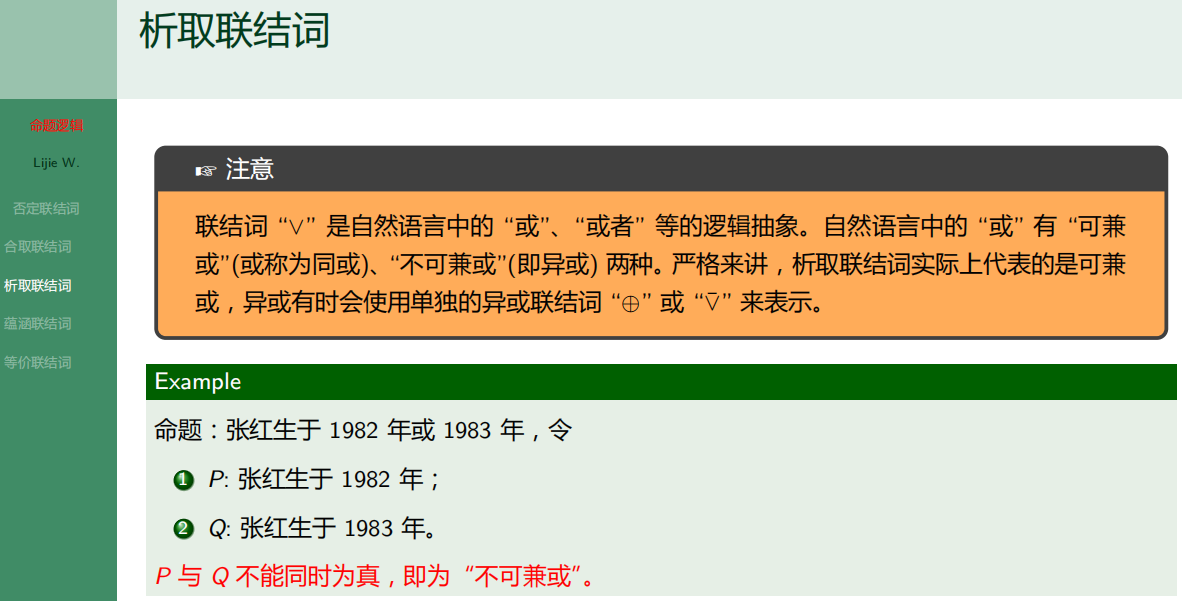
- 7.2.3 析取联结词
- 7.2.4 蕴涵联结词
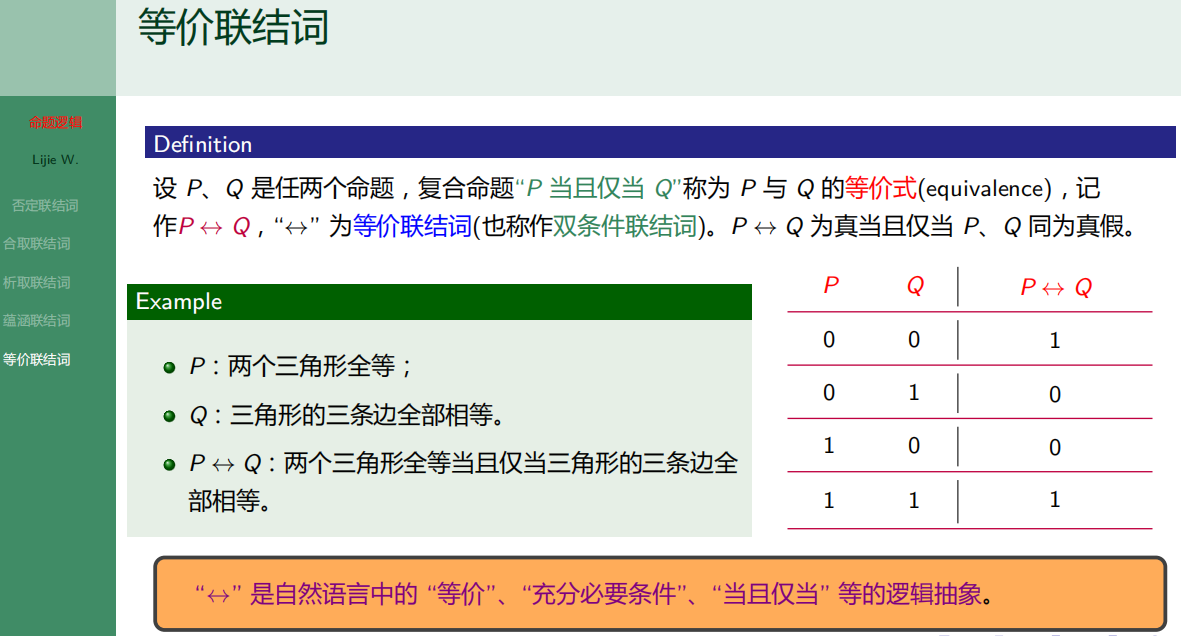
- 7.2.5 等价联结词
- 7.3 命题逻辑-命题符号化及应用
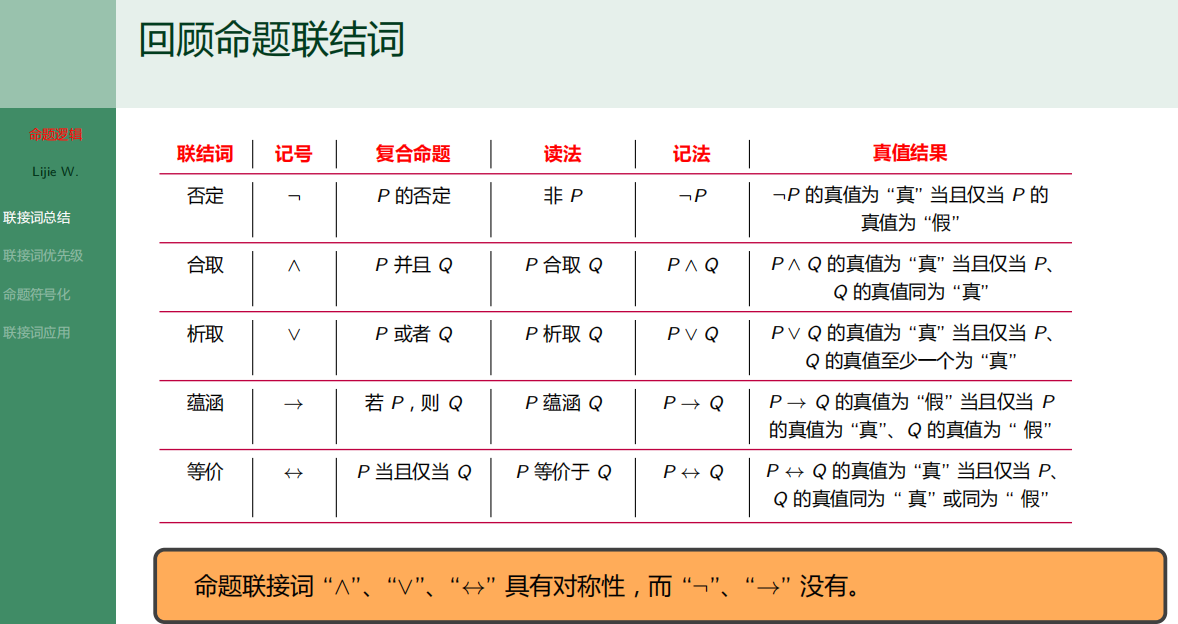
- 7.3.1 联结词总结
- 7.3.2 命题联结词优先级
- 7.3.3 命题符号化
- 7.3.4 联结词应用
- 7.4 命题逻辑-命题公式和真值表
- 7.4.1 命题变元
- 7.4.2 命题公式
- 7.4.3 公式的解释
- 7.4.4 真值表
- 7.5 命题逻辑-公式的分类和逻辑等价
- 7.5 命题公式的分类
- 7.5.2 公式的逻辑等价
- 7.6 命题逻辑-基本等价关系及其应用
- 7.6.1 基本等价关系
- 7.6.2 判断公式类型
- 7.6.3 证明公式等价
- 7.6.4 开关电路化简
- 7.6.5 逻辑电路化简
- 7.6.6 智力游戏
- 7.7 命题逻辑-公式的标准型-范式
- 7.7.1 范式定义
- 7.7.2 范式求解
- 7.8 命题逻辑-基本推理形式和蕴涵公式
- 7.8.1 推理的基本形式
- 7.8.2 基本蕴涵关系
- 7.9 命题逻辑-自然演绎法推理
- 7.9.1 推理规则
- 7.9.2 演绎法推理
- 7.9.3 推理的应用
本文为离散数据与组合数学电子科技大学王丽杰老师的课程笔记,详细视频参考
【电子科技大学】离散数学(上) 王丽杰
【电子科技大学】离散数学(下) 王丽杰
latex的离散数学写法参考: 离散数学与组合数学-01
离散数学公式
!符号 代码 含义
∧
\wedge
∧ \wedge 且
∨
\vee
∨ \vee 或
∩
\cap
∩ \cap 交
∪
\cup
∪ \cup 并
⊆
\subseteq
⊆ \subseteq 子集
⊈
\nsubseteq
⊈ \nsubseteq 不是子集
⊂
\subset
⊂ \subset 真子集
⊄
\not\subset
⊂ \not\subset 不是真子集
∈
\in
∈ \in 属于
∉
\not\in
∈ \not\in 不属于
↔
\leftrightarrow
↔ \leftrightarrow 等价
⇔
\Leftrightarrow
⇔ \Leftrightarrow 等值
¬
\neg
¬ \neg或\lnot 非
R
\mathbb{R}
R \mathbb{R} 实数集
Z
\mathbb{Z}
Z \mathbb{Z} 整数集
∅
\varnothing
∅ \varnothing 空集
∀
\forall
∀ \forall 对任意的
∃
\exists
∃ \exists 存在
≥
\geq
≥ \geq大于等于
≤
\leq
≤ \leq 小于等于
下标的输入命令是:
x
内容
x_{内容}
x内容 x_{内容}
上标的输入命令式:
x
2
x^2
x2 x^2
空格 \quad
R / R\mkern-10.5mu/ R/ R\mkern-10.5mu/ 数值越大,斜杆越往字母左侧移动
离散数学与组合数学-07命题逻辑
7.1 命题逻辑-什么是命题
7.1.1 数理逻辑发展
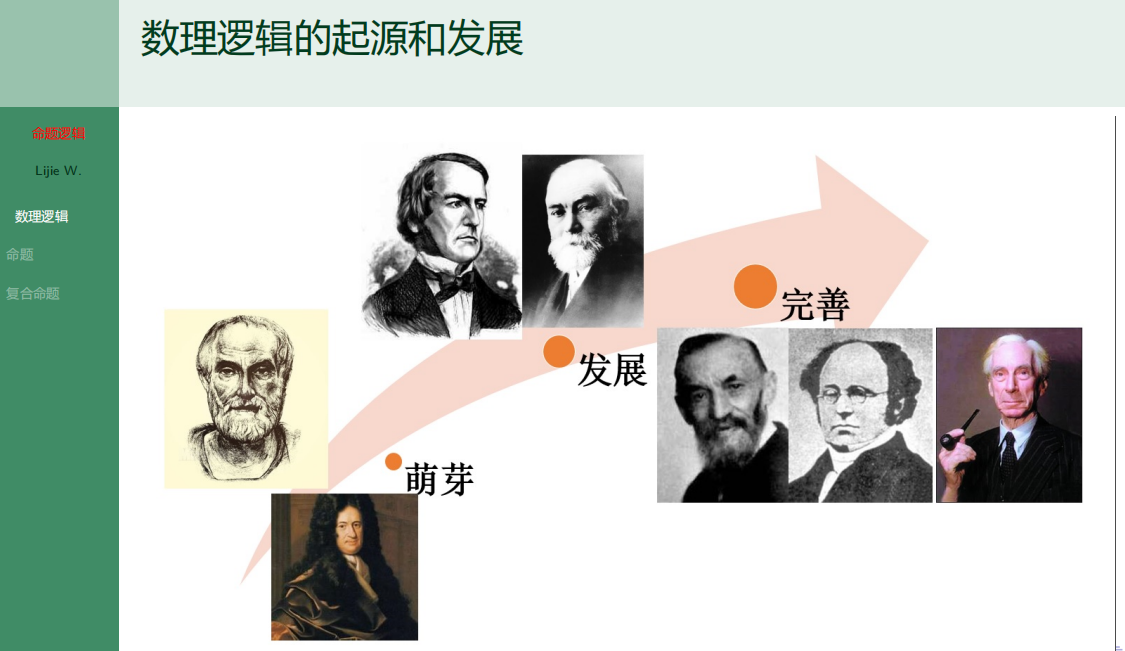
7.1.2 什么是命题

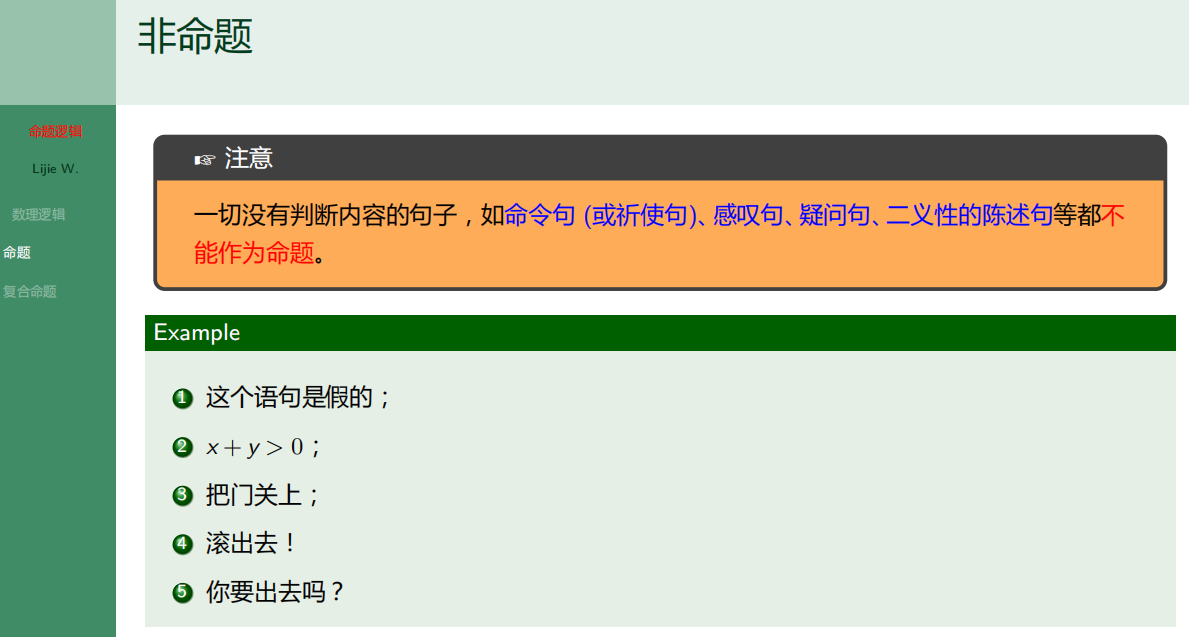
7.1.3 复合命题

7.2 命题逻辑-命题联结词
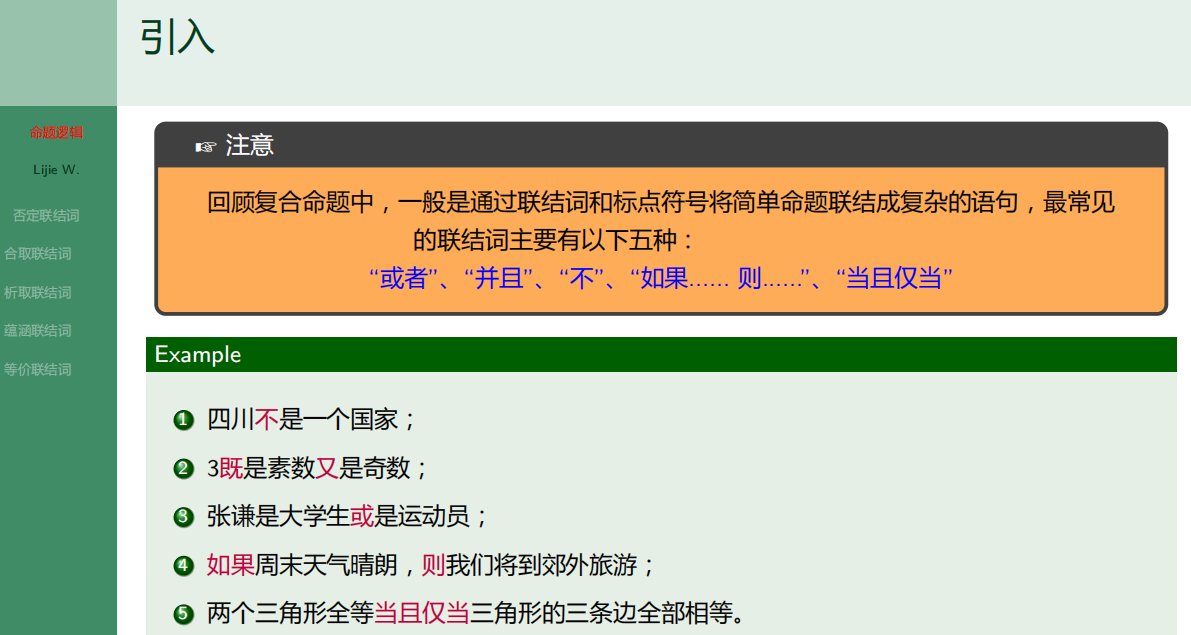
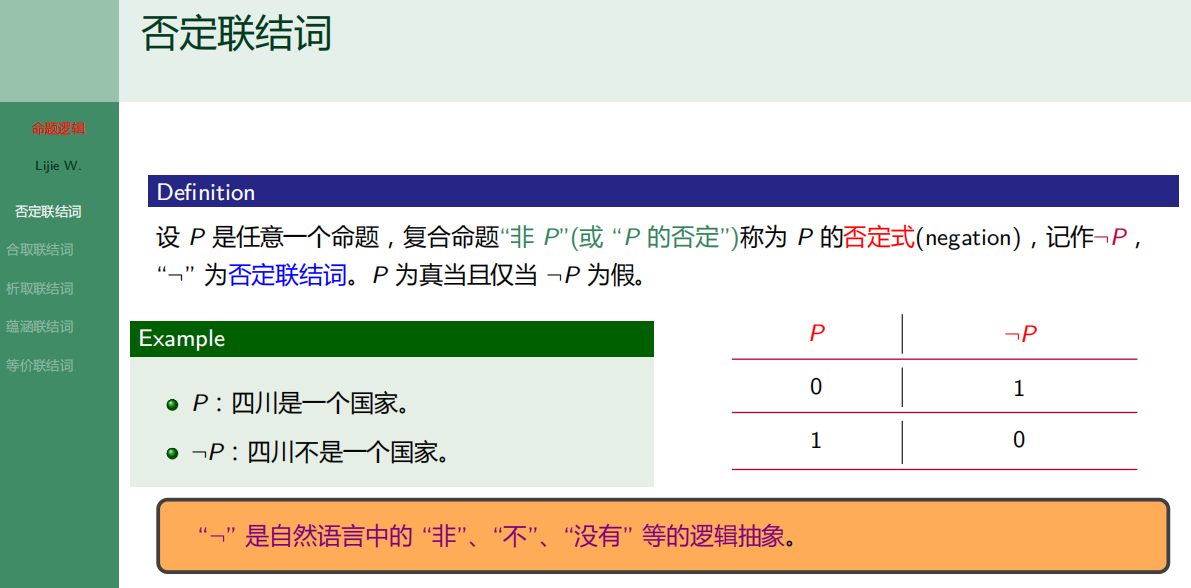
7.2.1 否定联结词
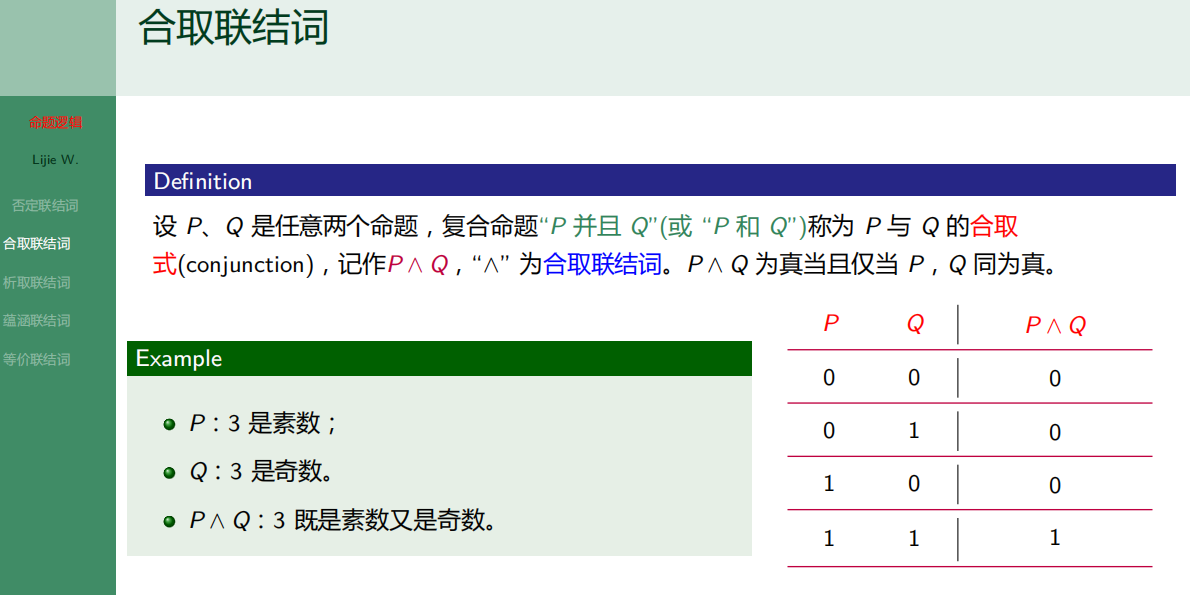
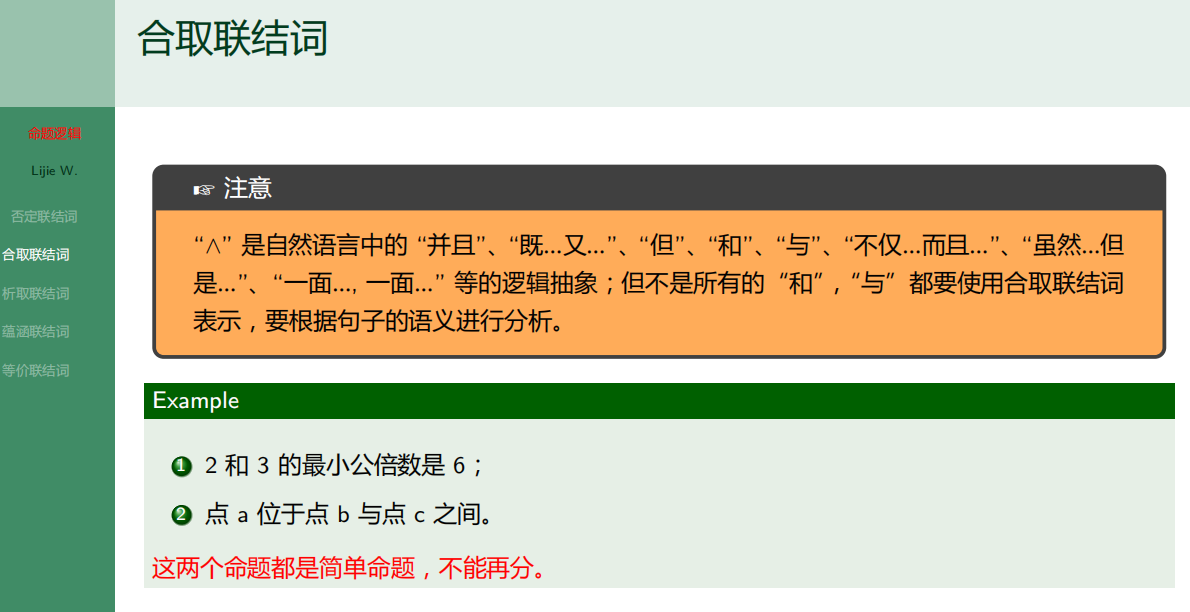
7.2.2 合取联结词
7.2.3 析取联结词
7.2.4 蕴涵联结词



7.2.5 等价联结词
7.3 命题逻辑-命题符号化及应用
7.3.1 联结词总结
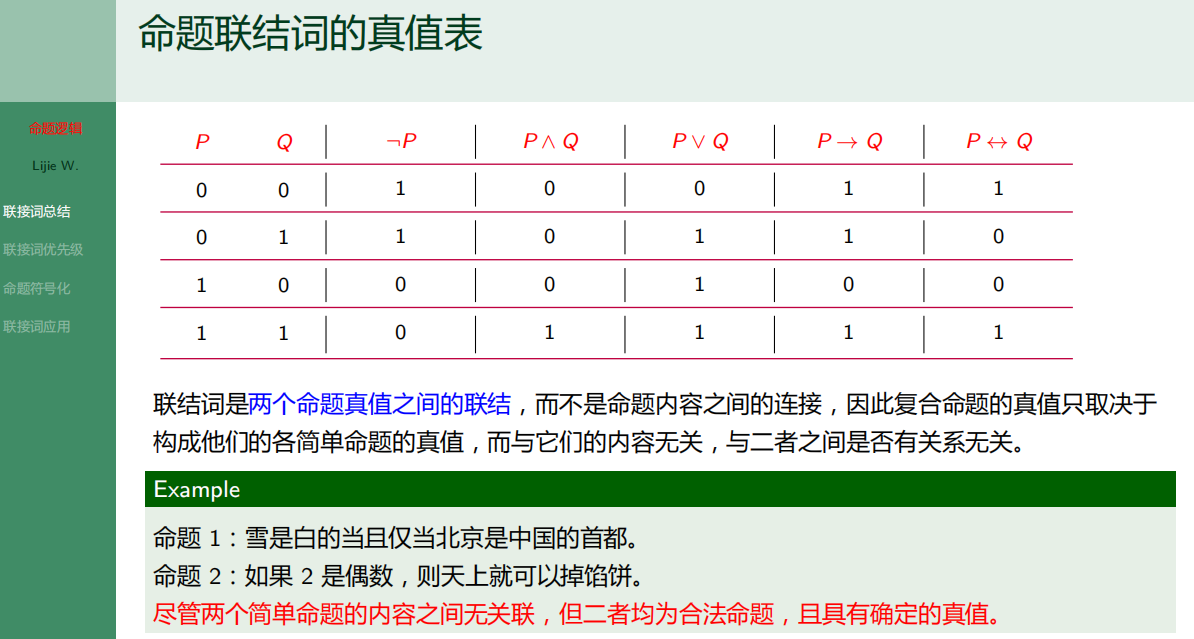
7.3.2 命题联结词优先级

7.3.3 命题符号化

7.3.4 联结词应用
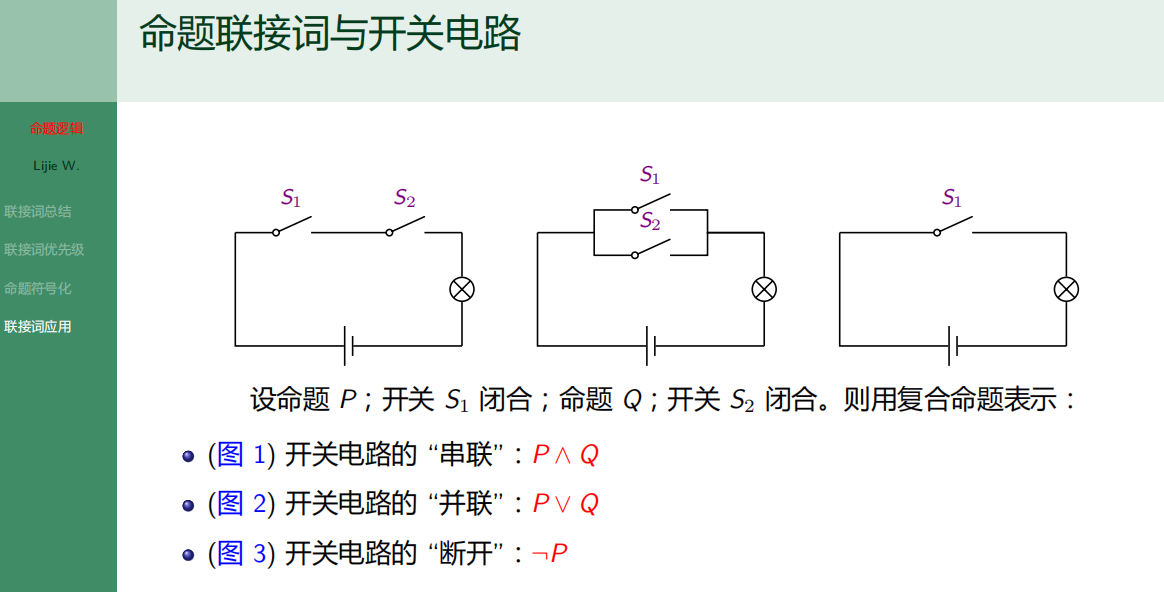


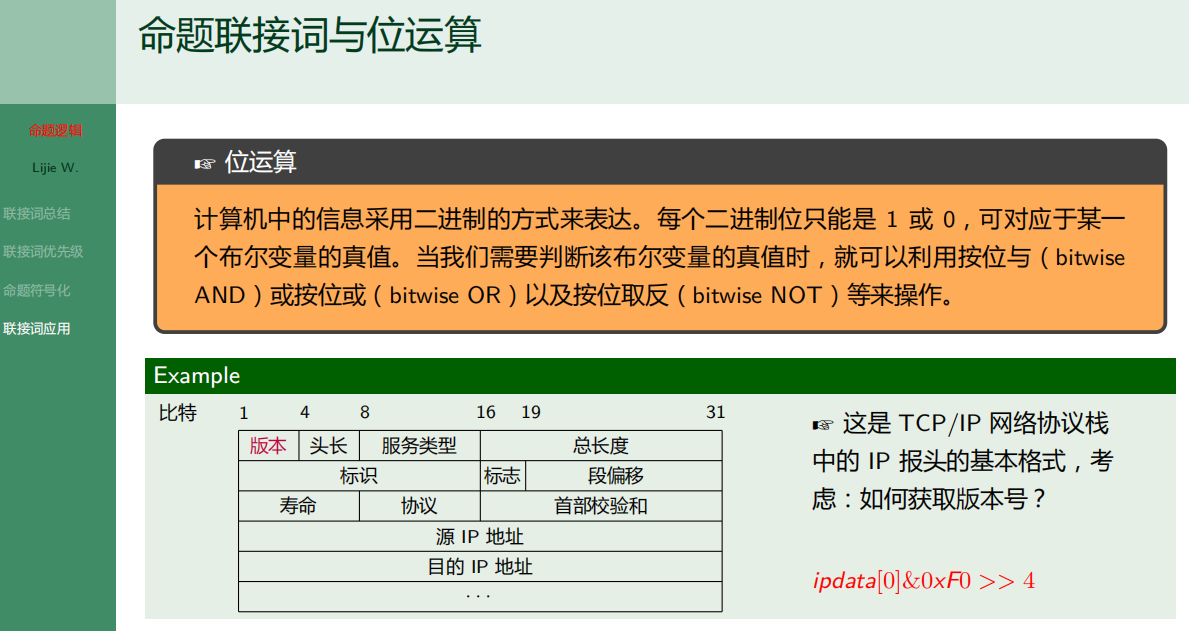
7.4 命题逻辑-命题公式和真值表
7.4.1 命题变元

7.4.2 命题公式

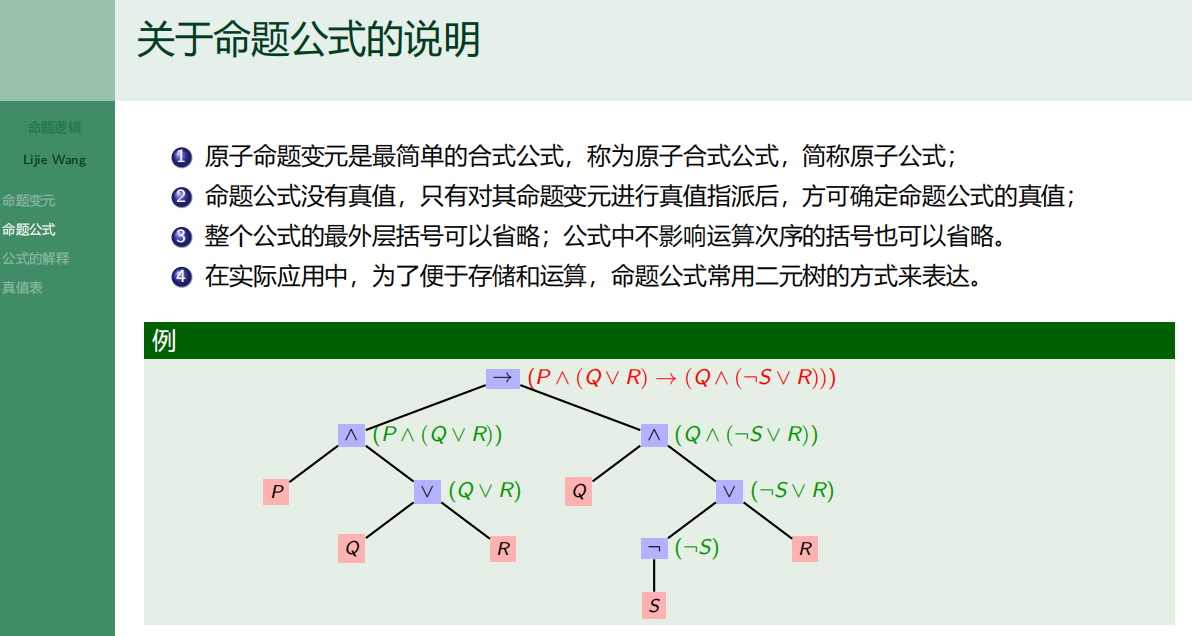
7.4.3 公式的解释

7.4.4 真值表

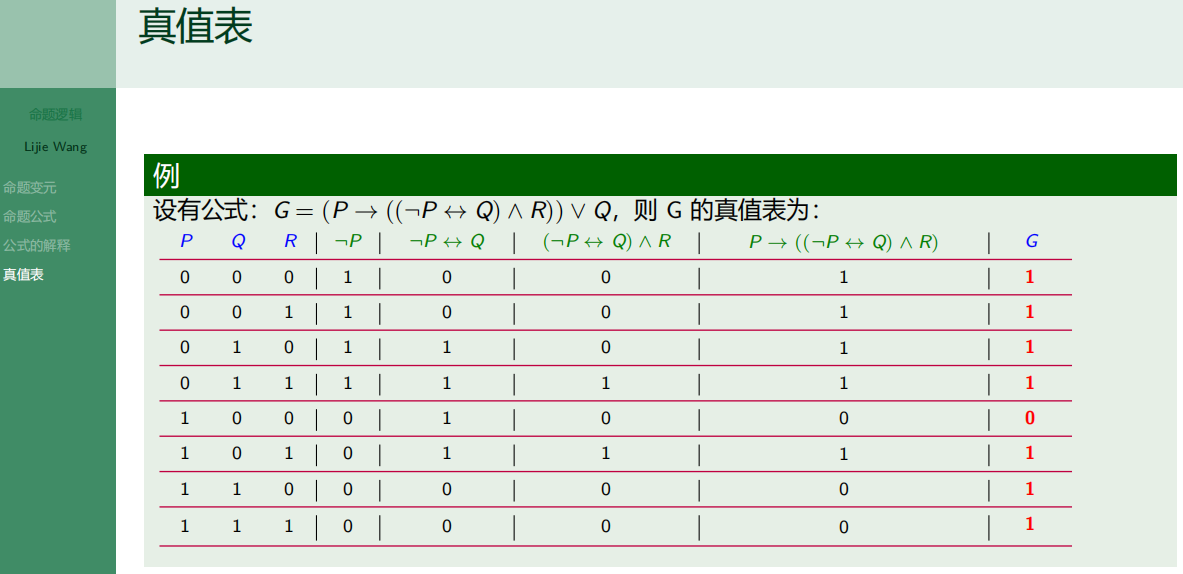
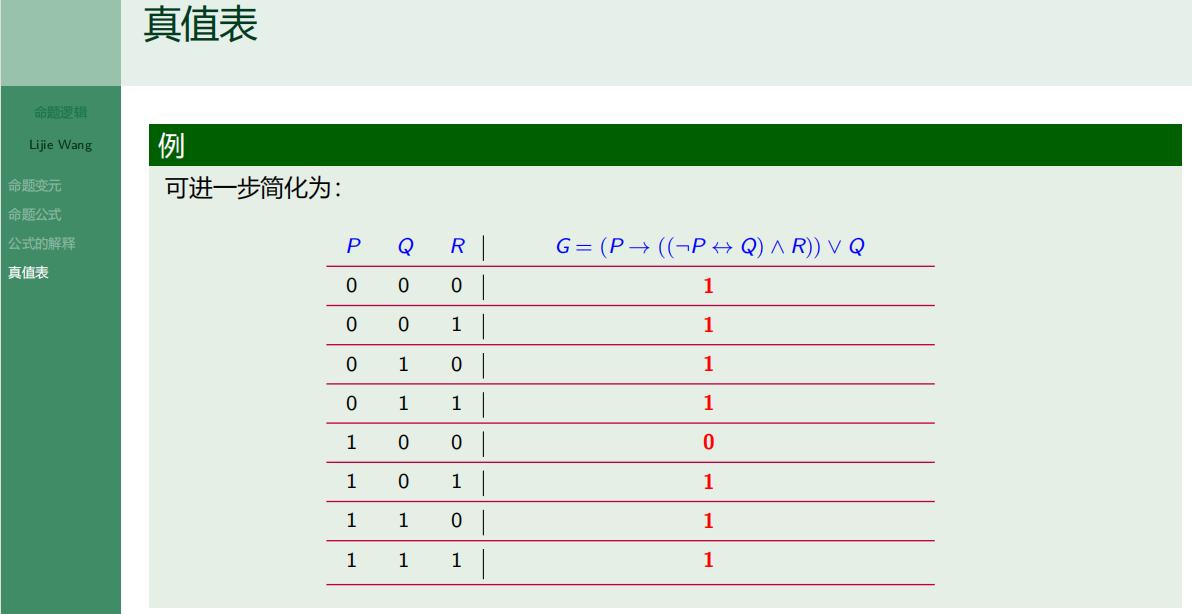
7.5 命题逻辑-公式的分类和逻辑等价
7.5 命题公式的分类


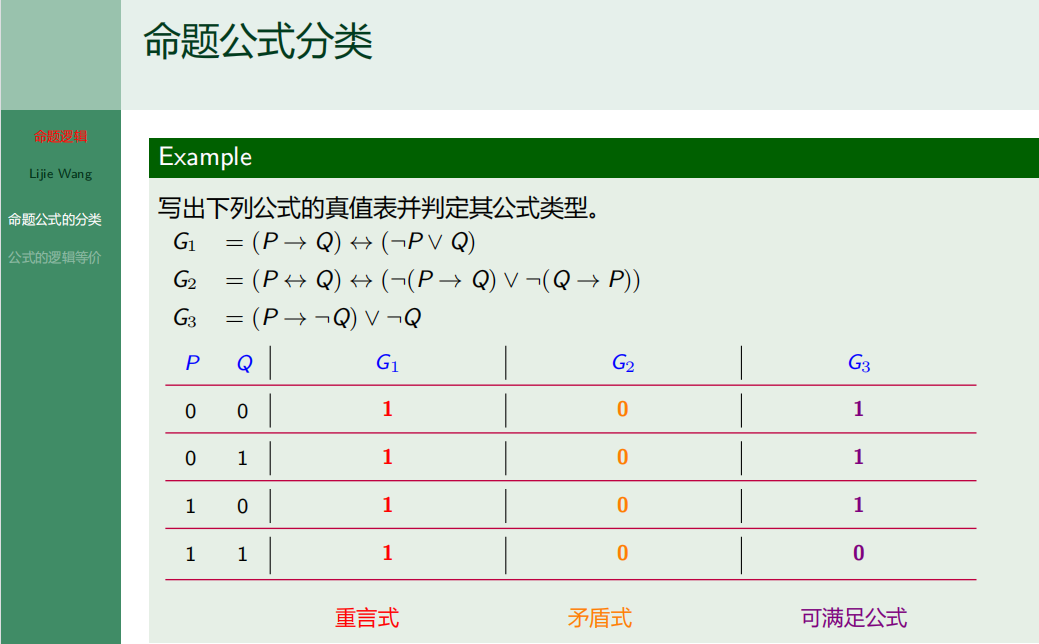
7.5.2 公式的逻辑等价


7.6 命题逻辑-基本等价关系及其应用
7.6.1 基本等价关系



7.6.2 判断公式类型

7.6.3 证明公式等价

7.6.4 开关电路化简
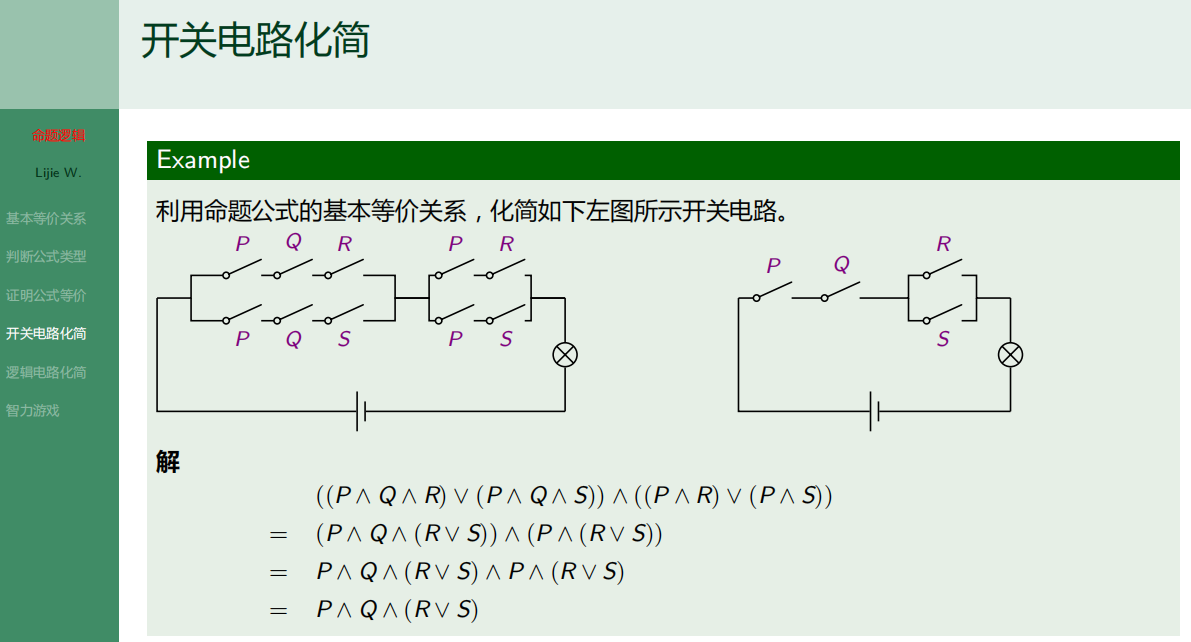
7.6.5 逻辑电路化简
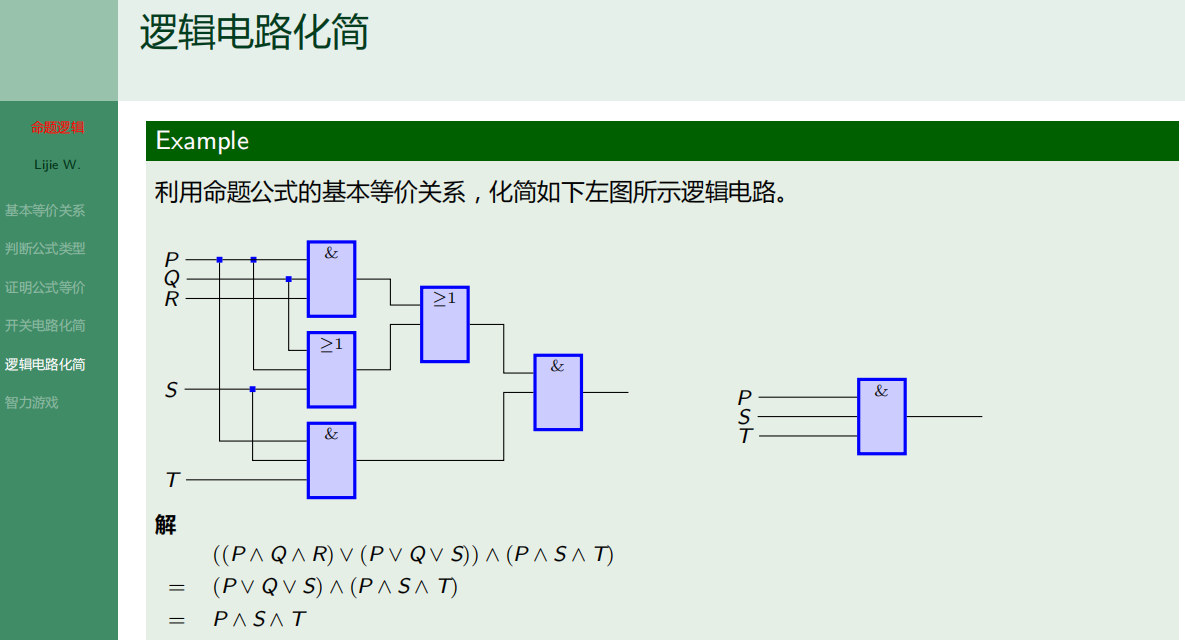
7.6.6 智力游戏
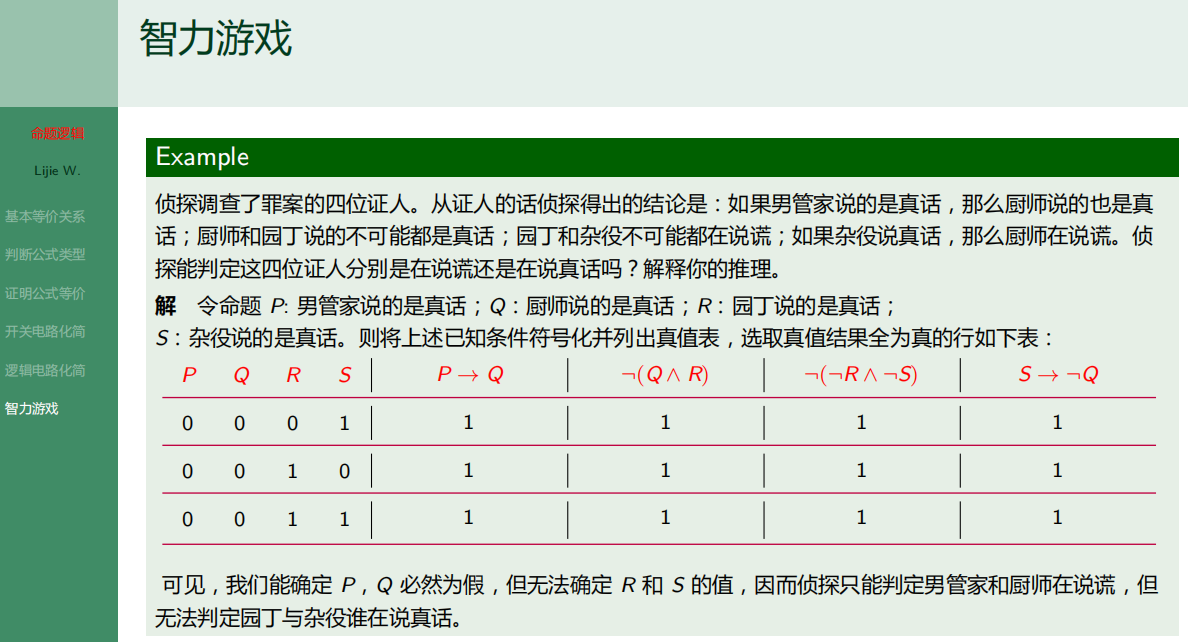
7.7 命题逻辑-公式的标准型-范式
7.7.1 范式定义


7.7.2 范式求解




7.8 命题逻辑-基本推理形式和蕴涵公式
7.8.1 推理的基本形式



7.8.2 基本蕴涵关系


7.9 命题逻辑-自然演绎法推理
7.9.1 推理规则

7.9.2 演绎法推理



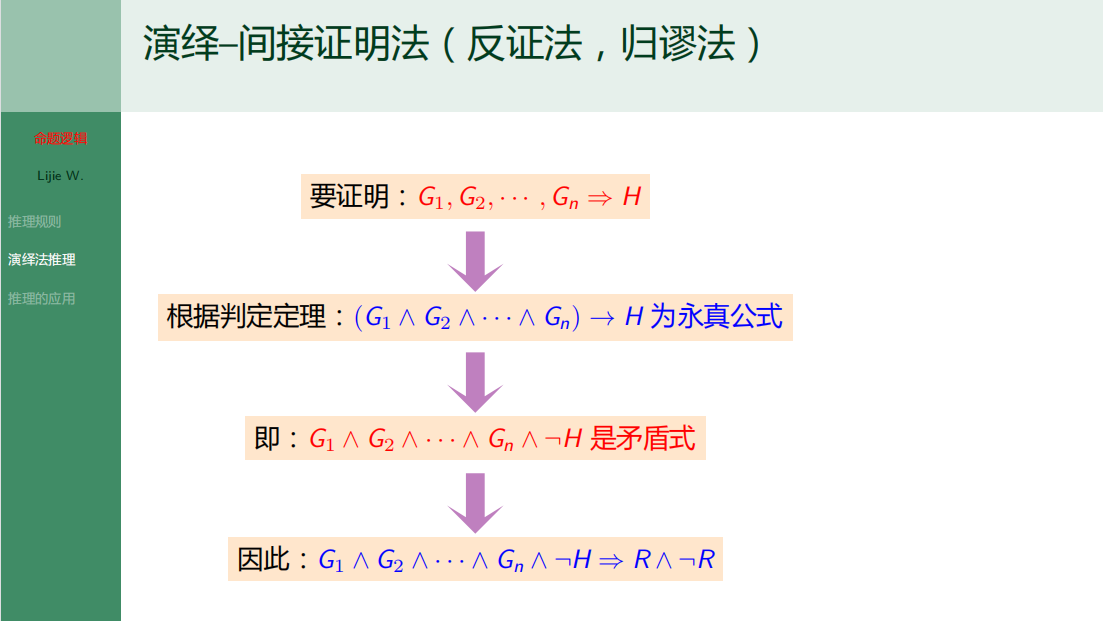
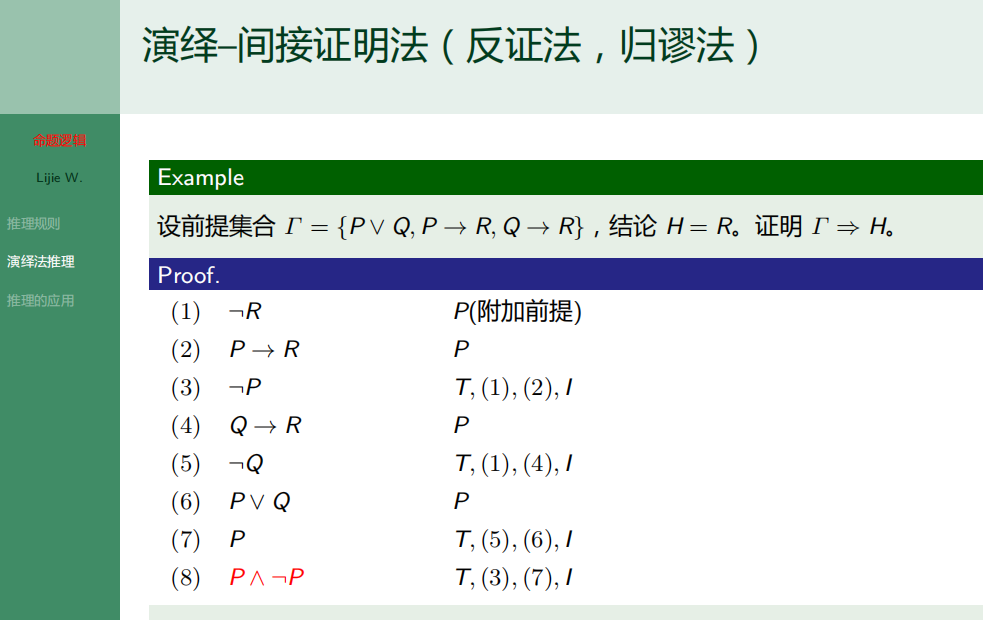

7.9.3 推理的应用