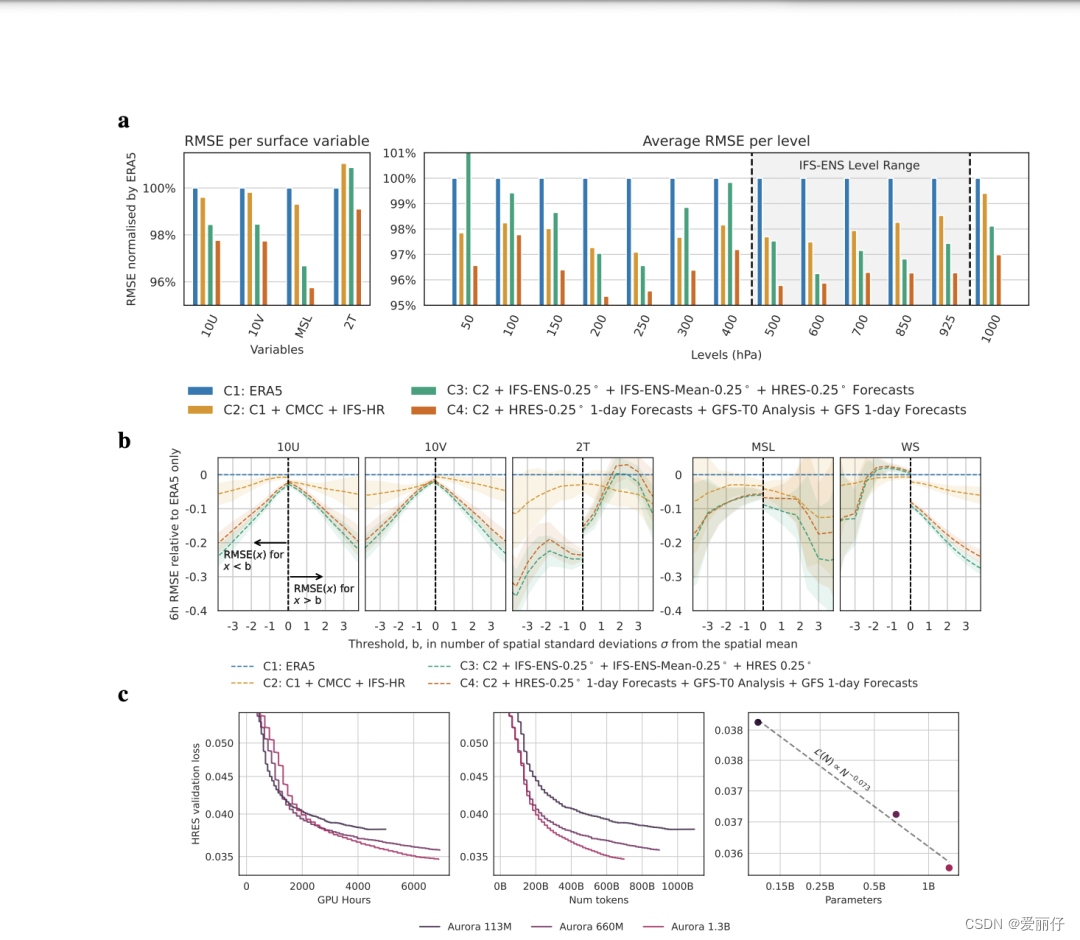
EFuse概念解析
EFUSE Key Parameter
iNOM 代表的是,Efuse运行时候的电流
tNOM 代表的是,Efuse电流与时间的曲线
INOM通过VOC_Thrs设置
VOC_THRS = VOC_THRS/Rsense
Vsense采样小于VOC_THRS时候不动作
Vsense采样大于VOC_THRS时候根据Efuse_I2T曲线来
EFUSE I2T 代表的是电流产生热能的表达式,可以理解为RMS
Melting I2T 代表的是熔断的电流
VHSC_THRS 硬件短路电流保护
VHSC_THRS=VHSC_THRS/Rsense
典型的Fuse I2t曲线计算如下所示

和几何图形计算方法是相同的
机械保险丝的I2T曲线
little Fuse贴片保险丝的曲线

在这里我用 **红线** 标注了保险丝的的熔断时间,使用1/8A的Fuse时候约20s Fuse熔断可以根据Grid格点去寻找熔断时间和电流
结论:通过I2T曲线就可以找出熔断快的保险丝
EFUSE 的I2T曲线
这里以VN1048为例
VOC_Thrs设置为6mV 当过流时候Rshunt电压超过6mV开始积分
VHSC_Thrs设置为160mV 当过流时候Rshunt电压超过160mV直接关断

VN1048 I2T曲线
我们看到30mV以上以及30mV以下都是0.02s 这个是ta的电流分辨率的问题,在这个区间内的电流都是0.02s后关断
看到当电流越大时候跳闸时间越快,所以总的I和T的乘积是不会变的,这就是I2T曲线的函意。
EFUSE NTC Function 电子保险丝NTC方程
相对于普通的FUSE EFUSE提供外部的NTC可以对EFUSE的 MOSFET 进行保护,当ADC采集到过温的阈值以后就会关闭内部外部MOSFET内部框图如下所示

BIAS 提供一个抬高电压,VBG给NTC提供一个基准在进到ADC,内部放大器同相端等于反向端。简单的计算如下所示,结论就是等于VBG和同相端的压差,其中321为预设,无需理会

calcpad代码:
V_BG = ? {3}
V_NTC = ? {2}
R = ? {1}
V_R = V_BG - V_NTC
[calcpadlink](https://calcpad.eu/)
总结
优点
EFUSE 相对于机械保险丝拥有了过压和过流以及过温保护的功能,
EFUSE自带各种保护功能以及诊断,可以让你更加了解你这个系统遇到的问题
缺点
EFUSE 的耐压通常比较低
供电也会麻烦
需要MCU配合
EFUSE 架构设计
再看手册的时候我就想如果外部实现I2T 我会怎么去实现,所以给大家画个简单的框图看看,因为是初版所以还是有很多不足,大家轻喷

当然使用MCU去采集电流做I2T是最简单的,如果让我设计芯片我可能就这种玩法了
好了今天就先聊到这里了