目录
合成控制作为线性回归的一种实现编辑
合成控制作为线性回归的一种实现
为了估计综合控制的治疗效果，我们将尝试构建一个类似于干预期之前的治疗单元的“假单元”。然后，我们将看到这个“假单位”在干预后的表现。合成控制和它所模仿的单位之间的区别在于治疗效果。
要使用线性回归做到这一点，我们将使用 OLS 找到权重。我们将最小化干预前期间供体池中单位的加权平均值与治疗单位之间的平方距离。
为此，我们需要的第一件事是将单位（在我们的例子中为状态）转换为列，将时间转换为行。由于我们有 2 个功能，cigsale 和 retprice，我们将它们堆叠在一起，就像我们在上图中所做的那样。我们将建立一个在干预前看起来很像加利福尼亚的合成控制，并看看它在干预后的表现如何。出于这个原因，重要的是我们只选择干预前的时期。在这里，这些功能似乎具有相似的规模，因此我们不会对它们做任何事情。如果特征的比例不同，一个是千位，另一个是小数，在最小化差异时，较大的特征将是最重要的。为避免这种情况，首先对它们进行扩展很重要。
features = ["cigsale", "retprice"]
inverted = (cigar.query("~after_treatment") # filter pre-intervention period
.pivot(index='state', columns="year")[features] # make one column per year and one row per state
.T) # flip the table to have one column per state
inverted.head()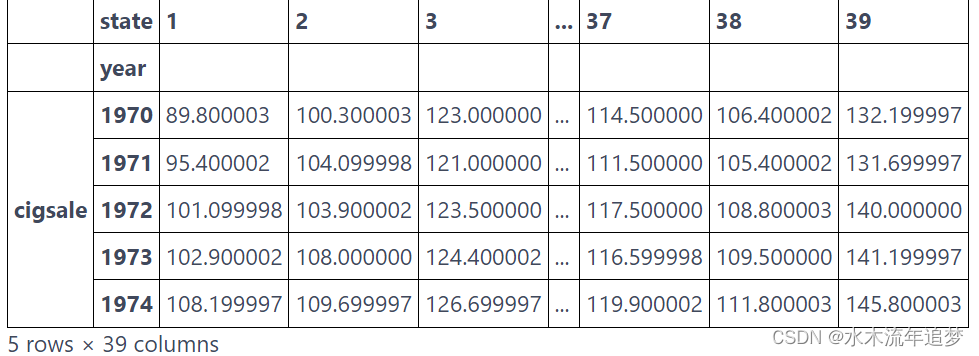
现在，我们可以将 Y 变量定义为加利福尼亚州，将 X 定义为其他州。
y = inverted[3].values # state of california
X = inverted.drop(columns=3).values # other states然后，我们运行回归。 有一个截距相当于添加另一个状态，其中每一行都是 1。你可以这样做，但我认为它更复杂，我就省略了。 回归将返回一组权重，以最小化治疗单位与供体池中单位之间的平方差。
from sklearn.linear_model import LinearRegression
weights_lr = LinearRegression(fit_intercept=False).fit(X, y).coef_
weights_lr.round(3)
array([-0.436, -1.038, 0.679, 0.078, 0.339, 1.213, 0.143, 0.555,
-0.295, 0.052, -0.529, 1.235, -0.549, 0.437, -0.023, -0.266,
-0.25 , -0.667, -0.106, -0.145, 0.109, 0.242, -0.328, 0.594,
0.243, -0.171, -0.02 , 0.14 , -0.811, 0.362, 0.519, -0.304,
0.805, -0.318, -1.246, 0.773, -0.055, -0.032])这些权重向我们展示了如何构建合成控制。 我们将状态 1 的结果乘以 -0.436，状态 2 的结果乘以 -1.038，状态 4 的结果乘以 0.679，依此类推。 我们可以通过池中状态的矩阵和权重之间的点积来实现这一点。
calif_synth_lr = (cigar.query("~california")
.pivot(index='year', columns="state")["cigsale"]
.values.dot(weights_lr))现在我们有了合成控制，我们可以用加利福尼亚州的结果变量来绘制它。
plt.figure(figsize=(10,6))
plt.plot(cigar.query("california")["year"], cigar.query("california")["cigsale"], label="California")
plt.plot(cigar.query("california")["year"], calif_synth_lr, label="Synthetic Control")
plt.vlines(x=1988, ymin=40, ymax=140, linestyle=":", lw=2, label="Proposition 99")
plt.ylabel("Gap in per-capita cigarette sales (in packs)")
plt.legend();
好吧……似乎有些不对劲。这张照片中什么吸引了你的注意力？首先，干预后，合成控制的卷烟销量超过了加州。这表明干预措施成功地降低了卷烟需求。其次，注意干预前的时期是如何完美拟合的。合成控制能够与加利福尼亚州完全匹配。这表明我们的综合控制模型可能过度拟合数据。另一个迹象是干预后综合控制结果变量的巨大差异。注意它是如何不遵循平滑模式的。相反，它会上下波动。
如果我们思考为什么会发生这种情况，请记住我们的供体池中有 38 个州。因此，我们的线性回归有 38 个参数可供使用，以使预处理池与处理尽可能接近。在这种情况下，即使 T 很大，N 也很大，这给我们的线性回归模型提供了太多的灵活性。如果您熟悉正则化模型，可以使用 Ridge 或 Lasso 回归来解决此问题。在这里，我们将研究另一种更传统的避免过拟合的方法。
