那一瞬间定格在记忆中
那一刹那感动到骨髓里
曾经
现在
将来
每一幅画,都是一个故事的开始,一段记忆的延续,它们承载着过去,映照着现在,启迪着未来。在艺术的世界里,每个人都能找到属于自己的那一幅画,那一幅能够触动心灵、刻进记忆的画。

梵高用《星夜》诠释了他对生命无尽的热爱和对宇宙深邃的探索
莫奈用《睡莲》展现了自然之美的宁静与和谐
毕加索用《格尔尼卡》诠释了战争的残酷和对和平的渴望
即使我们平凡的一生都有一幅画记忆或者向往……

嘉之音专注于将聚酯艺术融入生活。嘉之音中古风真丝彩绘画精选顶级桑蚕丝,通过热压工艺,将图案控制在1微米之内,突出真丝的天然纹理和光泽,使作品更具层次感,做到绘画与真丝完美融合,确保色彩的鲜艳和细节的完美呈现,让艺术的生命力在真丝上得到延续。嘉之音中古风真丝彩绘画不仅是一幅画作,更是一个故事、一段回忆、一种信念、一种向往。当凝望大师的名作,与之相关的记忆便会涌上心头,这些作品承载着灵魂,代表了“你”。

嘉之音真丝彩绘画还具备出色的吸音效果。它能够有效吸收室内噪音,降低回声改善声场均匀性,提高声音的清晰度和可听性,创造独特的视觉和听觉效果。无论是家居装饰,还是在酒店、咖啡厅等商业空间的布置,嘉之音真丝彩绘画都能完美融入,成为空间的点睛之笔。


一生一幅画,嘉之音中古风真丝彩绘画,让艺术不仅仅停留在记忆中,也代表你的向往、你的期望……
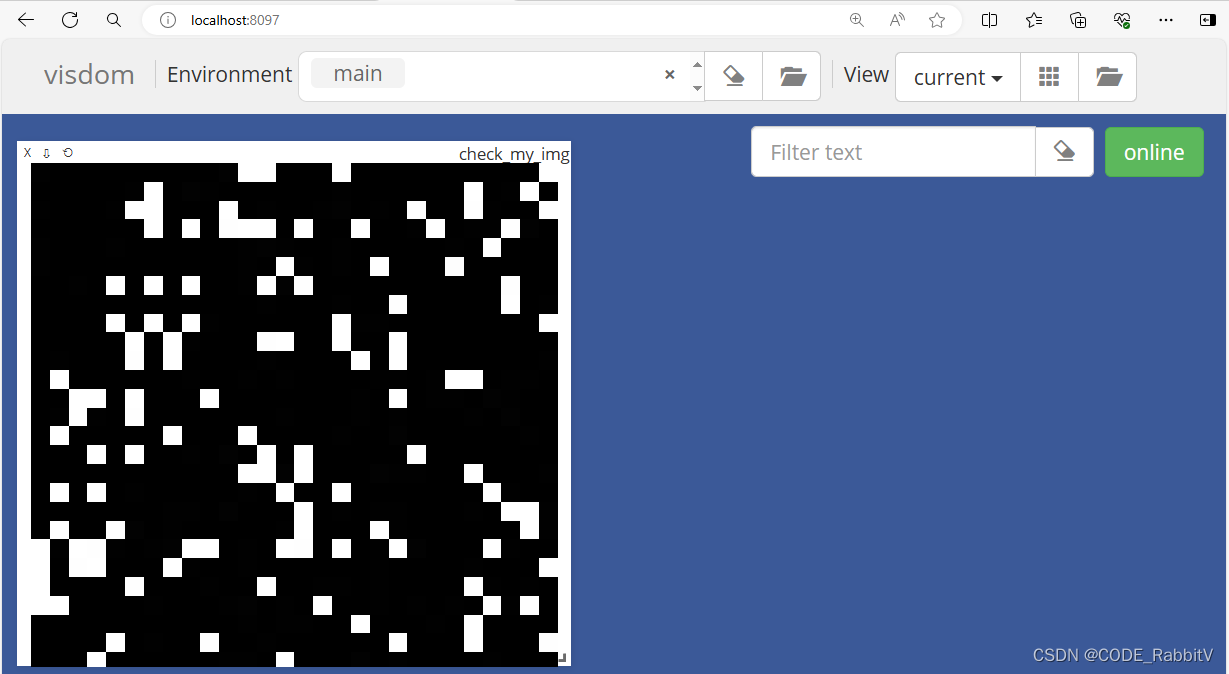





![[图解]《分析模式》漫谈02-第2章图的多重性错误](https://img-blog.csdnimg.cn/direct/1071b4e489da42239dd932444540cc72.png)