算法：模拟题目练习

题目一：替换所有的问号

题目二：提莫攻击

题目三：N字形变换

题目四：外观数列

题目五：数青蛙

首先先解释一下模拟算法是什么，其实模拟算法就是题目让我们干什么我们就干什么，思路比较简单，因为题目已经将解法告诉我们了，主要考察的就是代码能力，考察我们能不能根据这个思路转化成为代码，并且能不能将转化的代码进行优化

所以在做模拟算法题目时的步骤是：

①模拟算法流程(在草稿纸上过一遍流程)
②把流程转化成代码

题目一：替换所有的问号

给你一个仅包含小写英文字母和 '?' 字符的字符串 s，请你将所有的 '?' 转换为若干小写字母，使最终的字符串不包含任何 连续重复 的字符。

注意：你不能修改非 '?' 字符。

题目测试用例保证除 '?' 字符之外，不存在连续重复的字符。

在完成所有转换（可能无需转换）后返回最终的字符串。如果有多个解决方案，请返回其中任何一个。可以证明，在给定的约束条件下，答案总是存在的。

示例 1：

输入：s = "?zs"
输出："azs"
解释：该示例共有 25 种解决方案，从 "azs" 到 "yzs" 都是符合题目要求的。只有 "z" 是无效的修改，因为字符串 "zzs" 中有连续重复的两个 'z' 。

示例 2：

输入：s = "ubv?w"
输出："ubvaw"
解释：该示例共有 24 种解决方案，只有替换成 "v" 和 "w" 不符合题目要求。因为 "ubvvw" 和 "ubvww" 都包含连续重复的字符。

提示：

1 <= s.length <= 100
s 仅包含小写英文字母和 '?' 字符

这道题目要求很简单，就是给一个字符串，将字符串中的 ? 替换成小写字母，只要保证替换后不包含连续重复的字符即可，有多个方案返回一个即可

整体的算法思路就是：在 ? 这个位置，将 a~z 字符代入，判断是否会和 ? 前面或后面的字符重复，找到不重复的字符返回即可

有特殊情况， ? 在字符串最前面或是在字符串最后面，这时候就只需要比较一次即可

所以在 if 语句中，(i == 0 || ch != s[i-1])就表示，如果 i == 0 说明是首位，就不需要和前面的字符进行比较了，如果不是首位，在比较和前面的字符是否相等

(i == n-1 || ch != s[i+1])同理可得

代码如下：

class Solution {
public:
    string modifyString(string s) {
        int n = s.size();
        for(int i = 0; i < n; i++)
        {
            if(s[i] == '?')//替换
            {
                for(char ch = 'a'; ch <= 'z'; ch++)
                {
                    //特殊情况需要处理
                    if((i == 0 || ch != s[i-1]) &&(i == n-1 || ch != s[i+1]))
                    {
                        s[i] = ch;
                        break;
                    } 
                }
            }
        }
        return s;
    }
};

题目二：提莫攻击

在《英雄联盟》的世界中，有一个叫 “提莫” 的英雄。他的攻击可以让敌方英雄艾希（编者注：寒冰射手）进入中毒状态。

当提莫攻击艾希，艾希的中毒状态正好持续 duration 秒。

正式地讲，提莫在 t 发起攻击意味着艾希在时间区间 [t, t + duration - 1]（含 t 和 t + duration - 1）处于中毒状态。如果提莫在中毒影响结束前再次攻击，中毒状态计时器将会重置，在新的攻击之后，中毒影响将会在 duration 秒后结束。

给你一个 非递减 的整数数组 timeSeries ，其中 timeSeries[i] 表示提莫在 timeSeries[i] 秒时对艾希发起攻击，以及一个表示中毒持续时间的整数 duration 。

返回艾希处于中毒状态的总秒数。

示例 1：

输入：timeSeries = [1,4], duration = 2
输出：4
解释：提莫攻击对艾希的影响如下：
- 第 1 秒，提莫攻击艾希并使其立即中毒。中毒状态会维持 2 秒，即第 1 秒和第 2 秒。
- 第 4 秒，提莫再次攻击艾希，艾希中毒状态又持续 2 秒，即第 4 秒和第 5 秒。
艾希在第 1、2、4、5 秒处于中毒状态，所以总中毒秒数是 4 。

示例 2：

输入：timeSeries = [1,2], duration = 2
输出：3
解释：提莫攻击对艾希的影响如下：
- 第 1 秒，提莫攻击艾希并使其立即中毒。中毒状态会维持 2 秒，即第 1 秒和第 2 秒。
- 第 2 秒，提莫再次攻击艾希，并重置中毒计时器，艾希中毒状态需要持续 2 秒，即第 2 秒和第 3 秒。
艾希在第 1、2、3 秒处于中毒状态，所以总中毒秒数是 3 。

提示：

1 <= timeSeries.length <= 104
0 <= timeSeries[i], duration <= 107
timeSeries 按 非递减 顺序排列

这道题的意思就是说：题目会给一个中毒维持时间duration，表示每次会中毒几秒

如果在中毒期间还没结束时，又中毒，那么中毒时间就会重置，前面没有完全结束的时间就不用管了，只需要管新中毒的开始时间

例如示例2所示，数组中元素是1,2，说明在第1秒和第2秒都会中毒，本来第1秒中毒，会在第3秒时才正常，但是第2秒又中毒，所以此时只中毒了1秒，就被重置了，此时就不用管上次没有完成的中毒时间了，从第2秒开始中毒两秒后结束，所以总的时间就是1+2=3秒

所以总结一下：

假设有a、b、c三个中毒时间，中毒维持时间是d秒

那么如果 b - a >= d，说明a和b这两个中毒时间没有关联，b是在a中毒维持时间过了以后才中毒的
而如果 b - a < d，说明b是在a还没有中毒结束就又中毒了，此时只需要加上 b-a 的值，表示前一段的中毒时间即可

代码如下：

class Solution {
public:
    int findPoisonedDuration(vector<int>& timeSeries, int duration) {
        int n = timeSeries.size(), num = 0;
        if(n == 1) return duration;
        for(int i = 1; i < n; i++)
        {
            int tmp = timeSeries[i] - timeSeries[i-1];
            if(tmp >= duration) num += duration;
            else num += tmp;
        }
        return num + duration;
    }
};

题目三：N字形变换

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。

比如输入字符串为 "PAYPALISHIRING" 行数为 3 时，排列如下：

P   A   H   N
A P L S I I G
Y   I   R

之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如："PAHNAPLSIIGYIR"。

请你实现这个将字符串进行指定行数变换的函数：

string convert(string s, int numRows);

示例 1：

输入：s = "PAYPALISHIRING", numRows = 3
输出："PAHNAPLSIIGYIR"

示例 2：

输入：s = "PAYPALISHIRING", numRows = 4
输出："PINALSIGYAHRPI"
解释：
P     I    N
A   L S  I G
Y A   H R
P     I

示例 3：

输入：s = "A", numRows = 1
输出："A"

提示：

1 <= s.length <= 1000
s 由英文字母（小写和大写）、',' 和 '.' 组成
1 <= numRows <= 1000

这道题初一看，N字形变换，其实就是将题目所给的字符串，按照下面的方式一次列举出来，然后再从第一行开始每行读取出来：

题目所给的numRows是几，每一条黑线上就有几个数，最后按照绿色的虚线按顺序读取出来即可

解法一：模拟

给出一个长度为len的字符串，还给出一个n，这就表示所需要一个宽为n的矩阵，因为向下的黑线上最多存在4个数字，也就是整个矩阵只有4行，那么矩阵的列有多少呢？可以精准计算出来，但是太麻烦了，我们就权当需要len列，这样肯定是够用的

所以这种解法需要的时间复杂度和空间复杂度都是O(N*len)

如果题目对于空间复杂度有要求，那么这个方法就不能使用了

解法二：找规律

下面用字符串的下标表示某一个字符，观察下图找规律，其中字符串共16哥字符，n等于4：

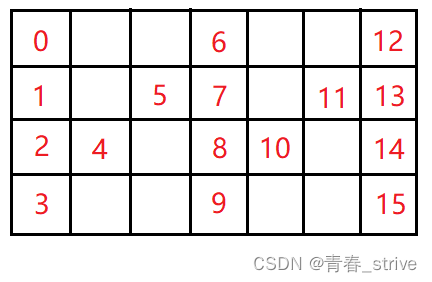
可以发现第 0 行和第 n-1 行中的数字公差d是6，也就是d = 2n - 2，相当于把5移动到第2列中，两列数字减去两个空格，就是公差，所以：

第0行： 0 -> 0+d -> 0+2d

第k行： (k, d-k) -> (k+d,d-k+d) -> (k+2d,d-k+2d)

第n-1行：n-1 -> n-1+d -> n-1+2d

除去第 0 行和第 n-1 行，中间的 k 行都是两个数字一个规律的

代码如下：

class Solution {
public:
    string convert(string s, int numRows) {
        if(numRows == 1) return s;//边界情况
        string ret;
        int n = s.size(), d = 2 * numRows - 2;
        //处理第0行
        for(int i = 0; i < n; i += d)
            ret += s[i];
        //处理中间行
        for(int k = 1; k < numRows - 1; k ++)//枚举每一行
        {
            //每次枚举两个字符
            for(int i = k,j = d-k; i < n || j < n; i+=d,j+=d)
            {
                if(i < n) ret += s[i];
                if(j < n) ret += s[j];
            }
        }
        //处理最后一行
        for(int i = numRows - 1; i < n; i += d)
            ret += s[i];
        return ret;
    }
};

题目四：外观数列

「外观数列」是一个数位字符串序列，由递归公式定义：

countAndSay(1) = "1"
countAndSay(n) 是 countAndSay(n-1) 的行程长度编码。

行程长度编码（RLE）是一种字符串压缩方法，其工作原理是通过将连续相同字符（重复两次或更多次）替换为字符重复次数（运行长度）和字符的串联。例如，要压缩字符串 "3322251" ，我们将 "33" 用 "23" 替换，将 "222" 用 "32" 替换，将 "5" 用 "15" 替换并将 "1" 用 "11" 替换。因此压缩后字符串变为 "23321511"。

给定一个整数 n ，返回 外观数列 的第 n 个元素。

示例 1：

输入：n = 4

输出："1211"

解释：

countAndSay(1) = "1"

countAndSay(2) = "1" 的行程长度编码 = "11"

countAndSay(3) = "11" 的行程长度编码 = "21"

countAndSay(4) = "21" 的行程长度编码 = "1211"

示例 2：

输入：n = 1

输出："1"

解释：

这是基本情况。

对于外观数列这个题意，除第1行外，下一行是对上一行的解释，即如果上一行是11，下一行就是21，21的含义是2个1：

第一行：1
第二行：11(一个1)
第三行：21(两个1)
第四行：1211(一个2，一个1)
第五行：111221(一个1，一个2，两个1)
第六行：312211(三个1，两个2，一个1)

如上即为所举示例的六行，下面的以此类推，括号中是解释

解法：模拟 + 双指针

模拟上述的过程，双指针是为了找连续相同的数的区间，便于解释

如果right与left相同，right就++，如果不同，就解释，然后left = right，以此类推

代码如下：

class Solution {
public:
    string countAndSay(int n) {
        string ret = "1";//第一行是固定的1
        for(int i = 1; i < n; i++)//解释n-1次
        {
            string tmp;
            int left = 0, right = 0;
            while(right < ret.size())
            {
                while(right < ret.size() && ret[right] == ret[left]) right++;
                int count = right - left;
                tmp += to_string(count) + ret[left];
                left = right;
            }
            ret = tmp;
        }
        return ret;
    }
};

题目五：数青蛙

给你一个字符串 croakOfFrogs，它表示不同青蛙发出的蛙鸣声（字符串 "croak" ）的组合。由于同一时间可以有多只青蛙呱呱作响，所以 croakOfFrogs 中会混合多个 “croak” 。

请你返回模拟字符串中所有蛙鸣所需不同青蛙的最少数目。

要想发出蛙鸣 "croak"，青蛙必须依序输出 ‘c’, ’r’, ’o’, ’a’, ’k’ 这 5 个字母。如果没有输出全部五个字母，那么它就不会发出声音。如果字符串 croakOfFrogs 不是由若干有效的 "croak" 字符混合而成，请返回 -1 。

示例 1：

输入：croakOfFrogs = "croakcroak"
输出：1 
解释：一只青蛙 “呱呱” 两次

示例 2：

输入：croakOfFrogs = "crcoakroak"
输出：2 
解释：最少需要两只青蛙，“呱呱” 声用黑体标注
第一只青蛙 "crcoakroak"
第二只青蛙 "crcoakroak"

示例 3：

输入：croakOfFrogs = "croakcrook"
输出：-1
解释：给出的字符串不是 "croak" 的有效组合。

提示：

1 <= croakOfFrogs.length <= 105
字符串中的字符只有 'c', 'r', 'o', 'a' 或者 'k'

这道题题意是 croak 代表一声蛙鸣，一只青蛙需要将 croak 这一声叫完才能叫第二声，所以看示例1，字符串是：croakcroak，一只青蛙croak叫完后，继续croak再叫一声，所以示例一最少需要一只青蛙

示例二：字符串是crcoakroak，可以通过我标记的颜色看出来，第一只青蛙还没有叫完的时候，也就是紫色的croak还没有结束时，绿色的croak出现了，所以绿色的croak需要另一只青蛙叫，所以示例二至少需要两只青蛙

示例三：croakcrook，紫色的croak代表一声蛙鸣，而后面的绿色字符串并不是croak，所以这个就不是有效组合，所以返回-1

以上即为题目的解释

解法一：模拟 + 哈希表(多个if/else判断)

因为青蛙每次叫的都是 croak，所以 roak 这4个字符每次都需要去哈希表中找一下前驱字符：
如果存在，那就前驱字符个数--，当前字符个数++
如果不存在，那就不需要遍历了，直接返回-1

如果遍历到 c 这个字符时，需要找最后一个字符 k 是否在哈希表中，表示是否有青蛙叫完后处于空闲状况：
如果存在，那就最后一个字符个数--，当前字符个数++
如果不存在，那就说明没有空闲青蛙，当前字符++即可

而当处理到最后的时候，如果哈希表中 croa 这4个字符的个数是否为0，如果都为0，就返回 k 字符的个数，如果存在就返回-1，说明不是有效组合

代码如下：

class Solution {
public:
    int minNumberOfFrogs(string croakOfFrogs) {
        string t = "croak";
        int hash[26] = {0};
        int n = croakOfFrogs.size();
        for(int i = 0; i < n; i++)
        {
            char ch = croakOfFrogs[i];
            if(ch == 'c')//字符c,只需要看字符k的个数
            {
                if(hash['k'-'a'] != 0) hash['k'-'a']--;
                hash['c'-'a']++;
            }
            else //表示是 roak 这4个字符
            {
                if(ch == 'r')//字符r,需要判断 c 是否有个数
                {
                    if(hash['c'-'a'] == 0) return -1;
                    hash['c'-'a']--;
                    hash[ch - 'a']++;
                }
                if(ch == 'o')//字符o,需要判断 r 是否有个数
                {
                    if(hash['r'-'a'] == 0) return -1;
                    hash['r'-'a']--;
                    hash[ch - 'a']++;
                }
                if(ch == 'a')//字符a,需要判断 o 是否有个数
                {
                    if(hash['o'-'a'] == 0) return -1;
                    hash['o'-'a']--;
                    hash[ch - 'a']++;
                }
                if(ch == 'k')//字符k,需要判断 a 是否有个数
                {
                    if(hash[0] == 0) return -1;
                    hash[0]--;
                    hash[ch - 'a']++;
                }
            }
        }
        //最后观察哈希表 croa 这4个字符的个数是否为0
        for(auto it : croakOfFrogs)
            if(hash[it - 'a'] != 0 && it != 'k') return -1;
        return hash['k'-'a'];
    }
};

解法二：模拟 + 哈希表(哈希表记录下标，哈希映射的方式)

上面的解法一使用了非常多的if、else语句，使得可读性不强，下面第二种方法：
同样采用数组模拟哈希表，并且加上一个哈希表unordered_map，用于映射青蛙叫的那几个字符的下标

解法二的数组模拟的哈希表只有5个元素，优化了解法一每次都需要 -'a' 来映射进数组中，变为了使用新加的unordered_map哈希表，得到对应字母的下标

代码如下：

class Solution {
public:
    int minNumberOfFrogs(string croakOfFrogs) {
        string t = "croak";
        int n = t.size();
        vector<int> hash(n);
        unordered_map<char, int> index;//映射x和x对应的下标
        for(int i = 0; i < n; i++)
            index[t[i]] = i;
        for(auto it : croakOfFrogs)
        {
            if(it == 'c')
            {
                if(hash[n-1] != 0) hash[n-1]--;
                hash[0]++;
            }
            else
            {
                int i = index[it];//根据映射关系，由字符得到下标
                if(hash[i - 1] == 0) return -1;
                hash[i - 1]--;
                hash[i]++;
            }
        }
        //最后观察哈希表 croa 这4个字符的个数是否为0
        for(int i = 0; i < n-1; i++)
            if(hash[i] != 0) return -1;
        return hash[n-1];
    }
};

模拟算法的题目到此结束