---

---

题目1 杨氏矩阵

有一个数字矩阵，矩阵的每行从左到右是递增的，矩阵从上到下是递增的，请编写程序在这样的矩阵中查找某个数字是否存在。
要求：时间复杂度小于O(N);

思路:
我们可以通过题目要求分析得到：矩阵最右上角的数是一行中最大的数，是一列中最小的数
我们可以将这个数和需要查找的数进行比较:
如果这个数比查找的数大，说明查找的数肯定不在这一列，往左查找。
如果这个数比查找的数小，说明该行肯定没有这个数，往下查找。

举例分析:
矩阵
1 2 3
4 5 6
7 8 9
如果我们要查找5
(1)先和最右上角的3进行对比，5比3大，3又是第0行最大的数，所以该行肯定没有5，往下查找。
查找的范围为:
4 5 6
7 8 9

(2)此时最右上角的数为6，6比5大，6这一列的数肯定都比6大，所以这一列肯定没有5，往左查找。
查找的范围为:
4 5
7 8

(3)此时最右上角的数为5，成功找到该数并打印出所在矩阵的位置。
其他情况依次类推。

代码如下:

#include <stdio.h>
#define N 3
int main()
{
	int arr[N][N] = { {1,2,3},{4,5,6},{7,8,9} };
	int num;
	int flag;
	while (scanf("%d", &num) != EOF)
	{
		int i = 0;
		int j = N - 1;			//开始的i和j定位到矩阵最右上角的数
		flag = 0;				//假设最开始找不到该数
		while(i < N && j >= 0)
		{
			if (arr[i][j] > num)//如果最右上脚的数比查找的数大，则可以不用再查找这一列
			{
				j--;
			}
			else if (arr[i][j] < num)
			{
				i++;
			}
			else
			{
				flag = 1;
				break;
			}
		}
		if (flag == 1)
		{
			printf("成功查找到该数,该数处于第 %d 行,第 %d 列\n", i + 1, j + 1);
		}
		else
		{
			printf("该矩阵中找不到该数\n");
		}
	}
	return 0;
}

结果如图:

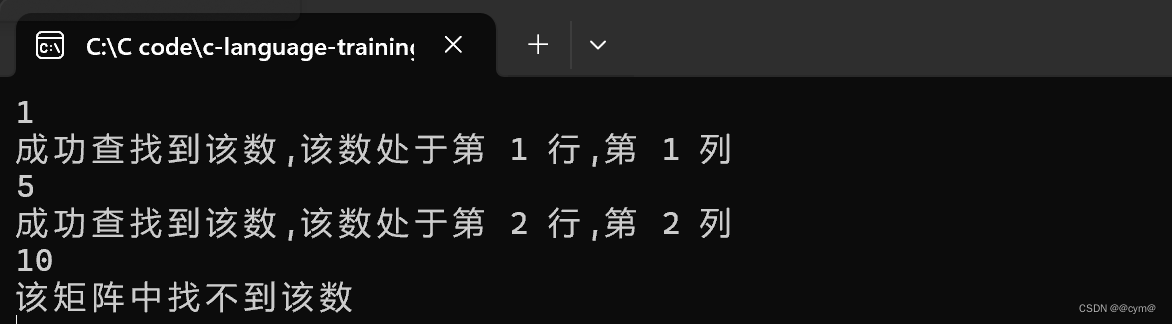
题目2 杨辉三角

在屏幕上打印杨辉三角：
1
1 1
1 2 1
1 3 3 1
……

思路:
首先我们观察杨辉三角的例子，可以找到规律:假设这是一个正方形，空白的地方对应的数是0，除去第一列的数都是1，每一行后面的每个数都是由上面一行该位置的数加上其前面的一个数之和。

我们可以发现，从第二行开始，每一行只和上面一行有联系，所以我们可以填一行的数组就打印一行，不用二维数组来解决，降低空间复杂度。

我们可以用一维数组的方式来实现，除去第一列，每一行后面的数的值等于当前位置的数加上前面一个位置的数之和。

因为我们每次将两个数相加时，要保证这两个数的值都没有被修改过
如果我们从左往右赋值，后面的数在进行相加的时候前面的数已经被修改了，会导致后面的数都是一样的，所以，我们需要从右往左依次计算结果。

举例分析:
假如我们想要输出杨辉三角前三行。
我们可以把杨辉三角看成
1 0 0
1 1 0
1 2 1
(0只是方便我们思考与计算，最终不用打印出来)
(1)首先每一列第一个数都是1，第一行直接打印1就行。
(2)此时数组的值分别为1 0 0，开始打印第二行，把第一行的数转换成第二行的数，可以发现第二行跟第一行的区别就是第二行第二个数是1，在第一行的基础上，我们可以将第二个数0和前面的1相加(标重的字体),将结果得到的1替换掉当前位置的0，然后直接输出，继续下一行的打印。
(3)此时数组的值分别为1 1 0，第三行后面两个数都和第二行不同，如果用刚才的思路，从左往右计算，那么，第三个数的计算就会变成0+2替换掉0，数组为1 2 2，显然不满足题目要求，第二个数先被修改了导致第三个数错误，所以，为了满足前面的数不被修改，我们需要从右往左计算。
(4)数组为1 1 0，首先计算第三个数，0+1=1，替换掉0，得到数组1 1 1，然后计算第二个数，1+1=2，替换掉当前位置的1，得到数组1 2 1，将第二行转换成第三行，之后输出结果。

代码如下:

#include <stdio.h>
#define N 10
int main()
{
	int arr[N] = { 1 };
	printf("1\n");						//第一行只有一个1，直接打印
	int i = 0;
	for (i = 1; i < N; i++)				//从第二行开始赋值
	{
		int j = 0;
		for (j = i; j > 0; j--)
		{
			arr[j] += arr[j - 1];		//从右往左依次计算
		}
		for (j = 0; j <= i; j++)
		{
			printf("%d ", arr[j]);
		}
		printf("\n");
	}
	return 0;
}