文章目录
- 一、Graham 凸包扫描算法
- 1、凸包概念
- 2、常用的凸包算法
- 3、Graham 凸包扫描算法
- 二、Graham 算法前置知识点
- 1、角排序
- 2、叉积
- 3、算法过程分析
- 三、代码示例
- 1、完整代码示例
- 2、执行结果
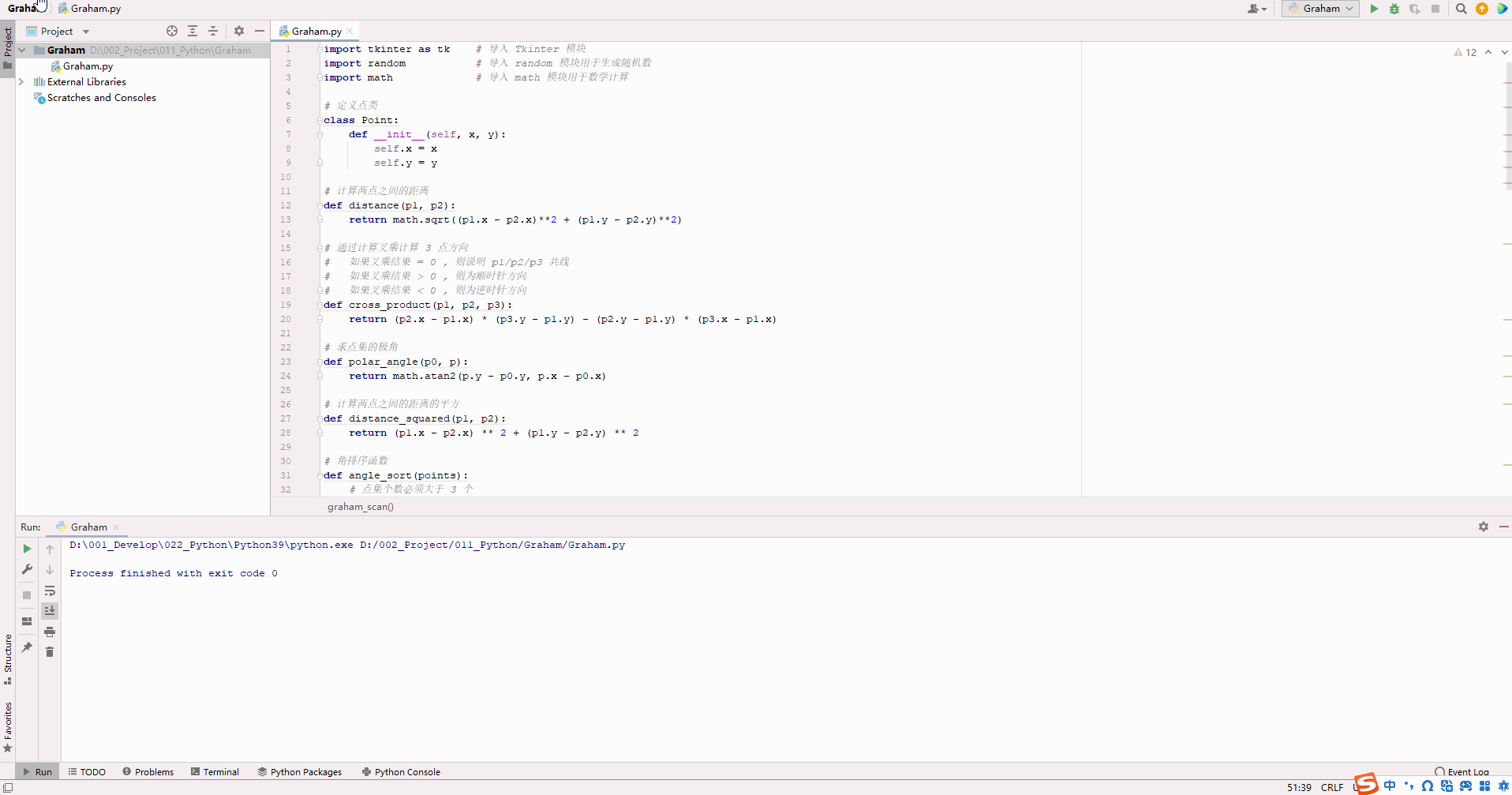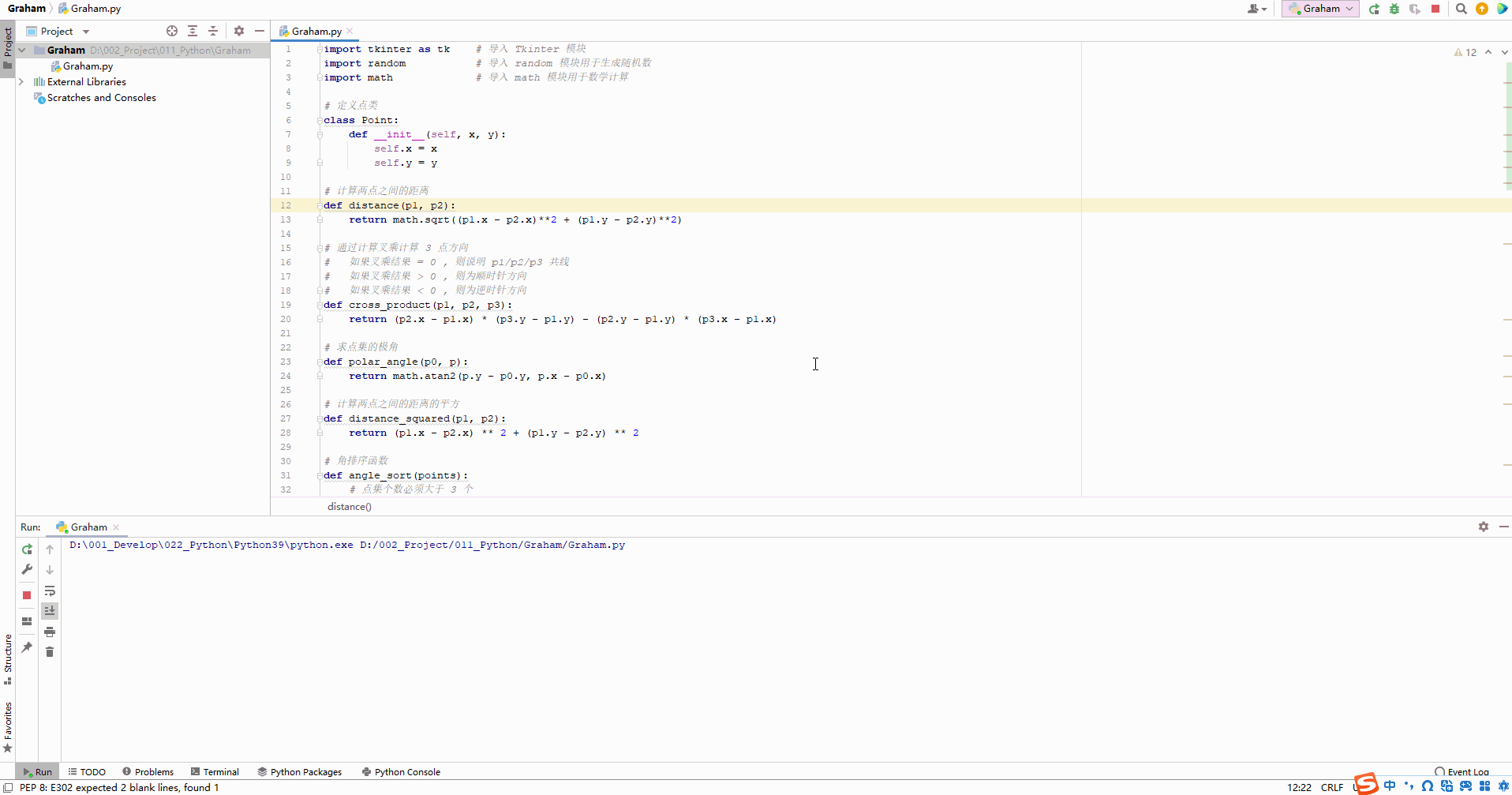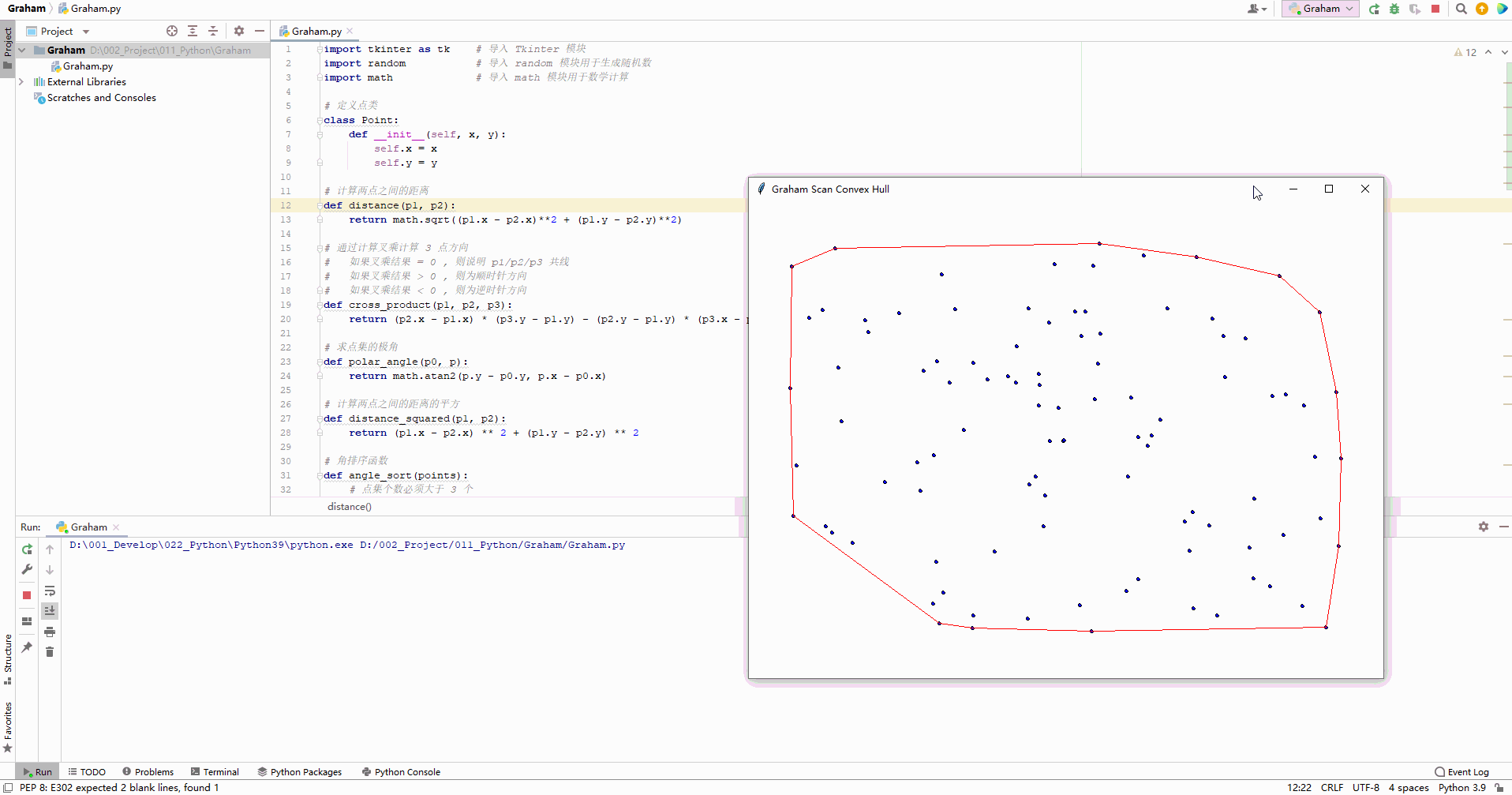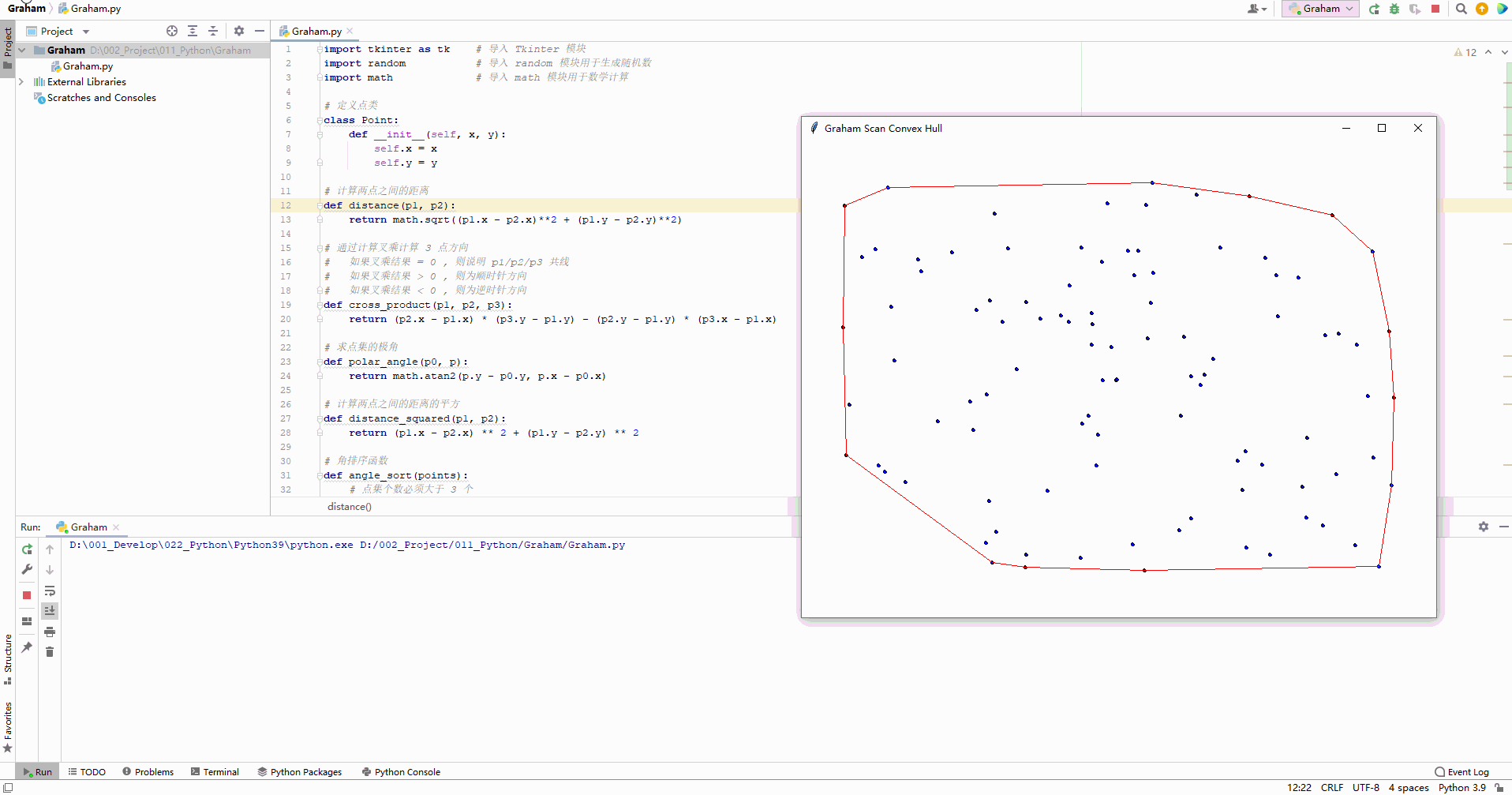
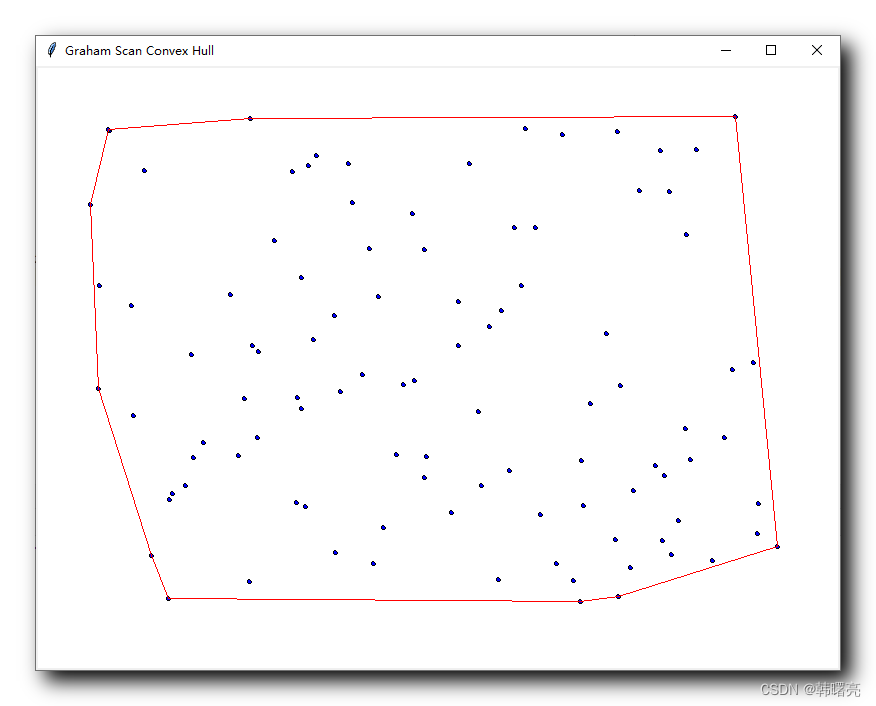
使用 Graham 算法绘制的凸包效果 :
博客代码下载 : https://download.csdn.net/download/han1202012/89428182
- 使用 PyCharm 打开 , 使用 Python 3.9 开发 ;
一、Graham 凸包扫描算法
1、凸包概念
凸包概念 : 在二维平面中 , 包围点集的最小凸多边形 , 其顶点集包含了给定点集中的所有点 , 并且不存在任何一条线段可以穿过这个多边形的内部而不与多边形的边界相交 ;
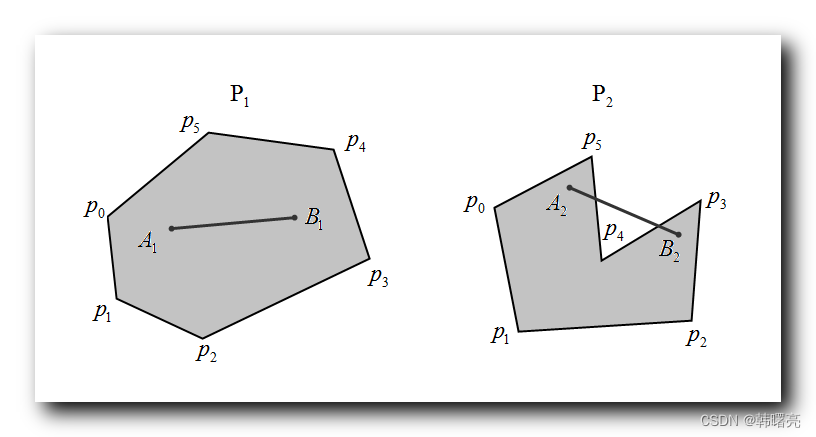
下图中 ,
- 左侧的 P1 图是凸包 ;
- 右侧的 P2 图不是凸包 , 因为该图中 , A2 到 B2 的点连接线与 凸多边形 的边界发生了相交 ;
2、常用的凸包算法
常用的凸包算法有 :
- Graham 扫描法
- Jarvis 步进法
- 快速凸包算法
3、Graham 凸包扫描算法
在二维平面上给出一个有限个点的点集 , 其坐标都为 (x , y) ;
Graham 格雷厄姆 凸包扫描算法 , 可以找到上述点集的 凸包边界 , 其时间复杂度是 O(nlogn) ;
二、Graham 算法前置知识点
1、角排序
角排序 是 以角度大小进行排序 , 这里的角度是 选定的基准点 与 点集中的点 的 极角 进行排序 ;
角排序 是一种在计算几何学和算法设计中常用的技术 , 用于对点集中的点按照其与某一基准点的极角进行排序 ;
极角 , 又称为 " 极坐标角度 " , 是指一个点相对于 极点 与 极轴 之间的夹角 , 极角通常用来描述点在 极坐标系 中的位置 ;
- 极点 是 中心的点 ;
- 极轴 是 水平 x 轴 ;
极坐标系如下图所示 , 一个点的位置由 极角 ( 从极轴到点到极点连线的方向的角度 ) 和 极径 ( 点到极点的距离 ) 确定 ;
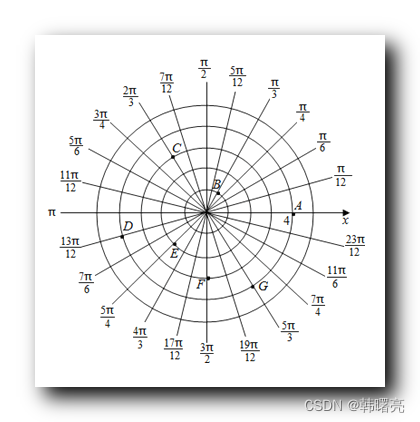
在角排序中 , 极角是指从基准点出发到其他点的连线与某一固定方向的夹角 ;
角排序用于解决凸包算法中的子问题 , 例如 Graham 扫描算法中 , 需要对点集中的点按照其与基准点的极角进行排序 , 以便确定凸包的边界顺序 ;
在本算法中 , 以极坐标的原点为中心 , 进行角排序 ;
2、叉积
叉积 , 又称为 " 向量积 " 或 " 矢量积 " , 是两个向量之间的一种运算 , 叉积 的结果是一个新的向量 , 值为两个向量所张成的平行四边形的面积 , 方向垂直于这个平行四边形的平面 , 符合右手定则 ;
判断 B 点 在 向量 OA 的左侧还是右侧 :
- B 在 向量 OA 左侧 , 则 OA 与 OB 的 叉积为负数 ;
- B 在 向量 OA 右侧 , 则 OA 与 OB 的 叉积为正数 ;
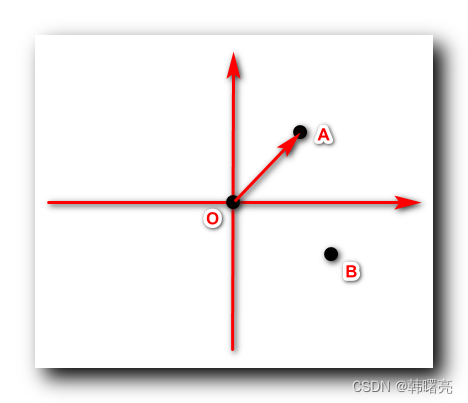
给定平面上 3 个点 ABC , 叉积 可以判断一个 点 C 在向量 AB 的哪一边 ,
- 如果 C 点在 向量 AB 左边 , 则 AB 与 AC 的叉积为正 ;
- 如果 C 点在 向量 AB 右边 , 则 AB 与 AC 的叉积为负 ;
3、算法过程分析
设置一个 栈 数据结构 ,
将左下角的 2 个点放入 栈 中 ,
从 第三个点开始循环 , 循环内容如下 :
先将要遍历的点放入 栈中 , 判断 新放入的点 是否在 栈顶 2 个元素组成的向量的左边 ,
- 如果在左边 , 说明该点是凸包上的点 , 栈中保留该点 , 则继续遍历下一个点 ;
- 如果在右边 , 说明该点不是凸包上的点 , 从栈中弹出该点 , 继续遍历下一个点 ;
三、代码示例
博客代码下载 : https://download.csdn.net/download/han1202012/89428182
- 使用 PyCharm 打开 , 使用 Python 3.9 开发 ;
1、完整代码示例
import tkinter as tk # 导入 Tkinter 模块
import random # 导入 random 模块用于生成随机数
import math # 导入 math 模块用于数学计算
# 定义点类
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
# 计算两点之间的距离
def distance(p1, p2):
return math.sqrt((p1.x - p2.x)**2 + (p1.y - p2.y)**2)
# 通过计算叉乘计算 3 点方向
# 如果叉乘结果 = 0 , 则说明 p1/p2/p3 共线
# 如果叉乘结果 > 0 , 则为顺时针方向
# 如果叉乘结果 < 0 , 则为逆时针方向
def cross_product(p1, p2, p3):
return (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x)
# 求点集的极角
def polar_angle(p0, p):
return math.atan2(p.y - p0.y, p.x - p0.x)
# 计算两点之间的距离的平方
def distance_squared(p1, p2):
return (p1.x - p2.x) ** 2 + (p1.y - p2.y) ** 2
# 角排序函数
def angle_sort(points):
# 点集个数必须大于 3 个
if len(points) < 2:
return points
# 找到最左下方的点作为起始点
# p0 点作为极坐标的原点
p0 = min(points, key=lambda p: (p.y, p.x))
# 按照极角和距离的平方排序
# 先按照极角进行排序 如果极角相同 则按照 p0 点到该点的距离排序
sorted_points = sorted(points, key=lambda p: (polar_angle(p0, p), distance_squared(p0, p)))
# 返回按照极角进行排序的 Point 集合
return [p0] + sorted_points[1:]
# Graham 扫描法找凸包
def graham_scan(points):
if len(points) < 3:
return points
# 进行角排序
sorted_points = angle_sort(points)
# 栈数据结构
stack = []
for p in sorted_points:
# 如果栈中的元素大于 2 个开始执行循环, 计算 p 点 在 栈顶两个元素(倒数第二个在前,倒数第一个再后)组成的向量的左侧还是右侧
while len(stack) >= 2 and cross_product(stack[-2], stack[-1], p) <= 0:
# 如果 p 点在栈顶两个元素组成的向量的左侧 则说明该点是凸边中的点 , 栈顶元素不是凸边中的点 , 将栈顶出栈 , 将本元素入栈
stack.pop()
# 向栈中添加新元素
stack.append(p)
return stack
# 生成随机点集
# 界面为 800x600 , x 方向上在 50 ~ 750 之间生成点, y 方向上在 50 ~ 550 之间生成点
def generate_points(num_points):
points = []
for _ in range(num_points):
x = random.randint(50, 750) # 生成 x 坐标范围在 50 到 750 之间的随机数
y = random.randint(50, 550) # 生成 y 坐标范围在 50 到 550 之间的随机数
points.append(Point(x, y))
return points
# 在画布上绘制点
def draw_points(canvas, points):
for point in points:
canvas.create_oval(point.x - 2, point.y - 2, point.x + 2, point.y + 2, fill="blue") # 绘制圆点
# 在画布上绘制凸包
def draw_convex_hull(canvas, convex_hull):
for i in range(len(convex_hull)):
p1 = convex_hull[i]
p2 = convex_hull[(i + 1) % len(convex_hull)]
canvas.create_line(p1.x, p1.y, p2.x, p2.y, fill="red") # 绘制凸包的边
# 主函数
def main():
num_points = 100 # 点的数量设置为 200 个
points = generate_points(num_points) # 生成随机点集
convex_hull = graham_scan(points) # 使用 Graham 扫描法找凸包
root = tk.Tk() # 创建 Tkinter 窗口
root.title("Graham Scan Convex Hull") # 设置窗口标题
canvas = tk.Canvas(root, width=800, height=600, bg="white") # 创建画布
canvas.pack() # 将画布放置在窗口中央
draw_points(canvas, points) # 绘制点集
draw_convex_hull(canvas, convex_hull) # 绘制凸包
root.mainloop() # 进入 Tkinter 主循环
if __name__ == "__main__":
main() # 调用主函数
2、执行结果
执行上述代码后 , 在画面中随机生成了 100 个点 , 并进行 Graham 扫描算法 , 计算出了点集的凸集 , 绘制效果如下 :