1.真实的世界

         经过前面的变换，再到三角形遍历，深度缓存后，屏幕上每个像素都有了对应的颜色，显示的结果大概是如下左图的样子，我们发现物体每个面的颜色都一样，看起来不够真实。而如下右图显得更加真实，物体每个面看起来颜色不太一样。这就是着色(Shading)的效果。

                                        

        那么真实的世界是什么样的呢？如下图所示，物体在真实世界中存在各种不同的效果(材质)，比如反射，光滑度等等，这就是接下来要做的事情，也就是着色。

2.着色(Shading)

2.1着色的定义

        在图形学中，着色是对不同物体应用不同材质的过程。

        举一个简单的例子，最基础的着色模型，叫做Blinn-Phong反射模型。

        如上图所示，物体表面受光照影响分为环境光、漫反射和高光反射三部分，如果通过一种方式可以分析并表示一个光源的这三部分影响，那我们就可以通过计算得到如上图杯子的材质。

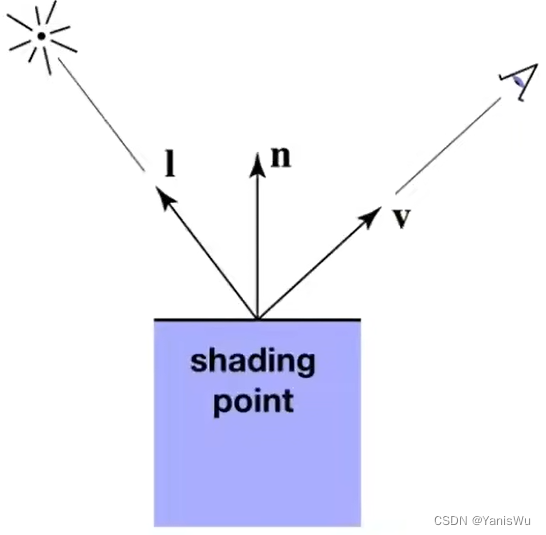
        如上图，我们把物体表面任意一点当做一个着色点(Shading point)，物体表面不一定是平整的，但是在局部一个极小范围内可以认为是一个平面。然后定义法线n，垂直于物体表面，v表示观测方向，通常指相机，i表示光源方向，看向光照的方向。定义的三个方向都可以做单位向量，后面出现默认都是指单位向量，长度是1。另外，还要定义物体表面的颜色(color)，光亮(shininess)。

着色是局部的

        着色是局部的，就是说任何一个点的着色情况，不考虑其他物体的存在，比如不考虑其他物体产生的阴影。如下图所示，红色指向位置着色不考虑其他物体产生的阴影。那么阴影如何生成，之后再说。

2.2着色模型

2.2.1漫反射

        如上图所示，一条光线打到物体表面某个点，会被均匀地反射到四面八方，这种现象叫作漫反射(Diffuse Reflection)。表面颜色所在所有观测方向都是一样的。但是为什么实际上，在同一个光源下，物体表面的亮度不尽相同呢？主要以下两个原因：

1.光源与表面法线夹角

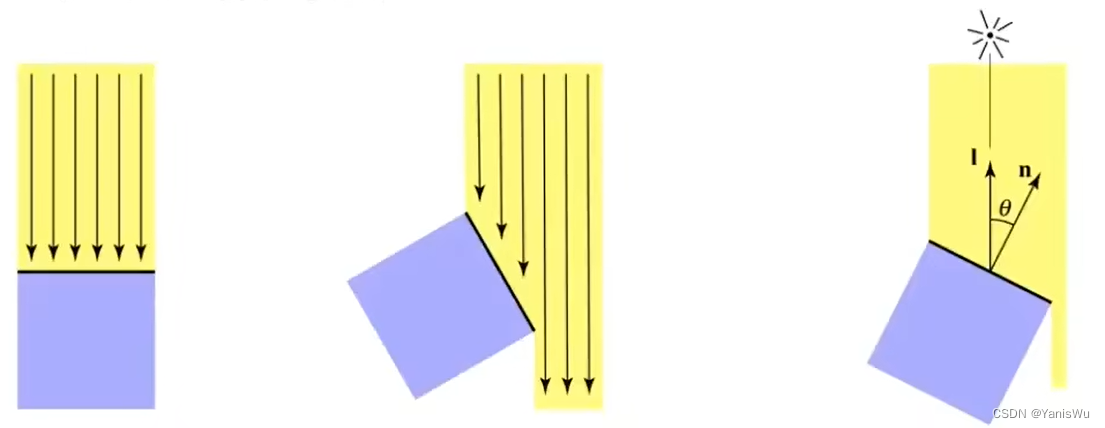
        如上图所示，假设一个光源有6根离散光线照射到物体表面，该表面大小为单位面积。当光线与物体表面垂直时，6根光线被物体表面全部接收，当物体表面与光线呈45度时，物体表面只能接收到一半的光线，只有一半能量，物体表面会暗一点。由此推出结论，物体接收光源能量的大小与光源与物体表面法线有关，成正比cosθ = l · n。

2.光源与着色点的距离(衰减)

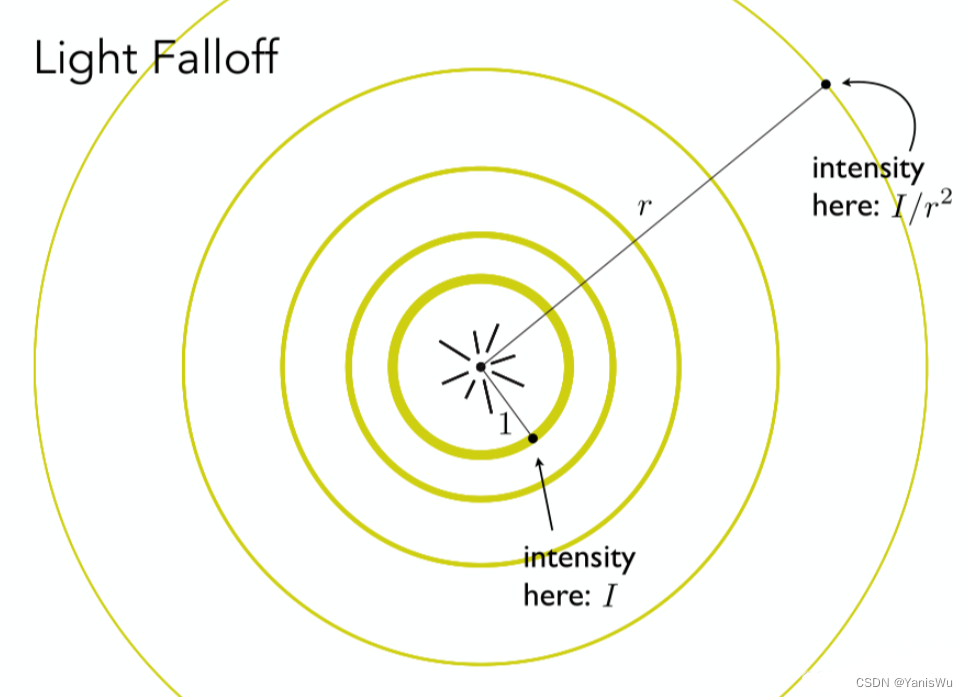
        如上图，假设光源位于中心，发射出的能量是I，随着时间的推移在三维空间中向周围均匀的辐射开来，图中的圆圈表示三维中的球壳，你会发现半径越大线越细，线的粗细表示能量的大小，从球心开始，半径越大球的表面面积越大，分到单位面积上的能量就越小。依据能量守恒定律(假设在真空传播，没有能量损失)，某一时刻球壳上的能量与上一时刻球壳上的能量是相等的，因此某一点的能量与球的半径的平方成反比。

漫反射模型

        依据上述理论，人们总结得到了漫反射的计算模型Ld = kd(I/)max(0,n·l)，它是经验模型。

        max(0,n·l)表示光线与物体表面法线夹角的影响，之所以使用max将点乘结果为负的结果排除，因为点乘结果为负数时，表示光源在物体表面的下方，计算光照没有意义。

        I/表示光照衰减。

        kd表示漫射射系数或漫反射光颜色，物体表面本身颜色。如下图为kd系数影响漫反射情况。

        漫反射与光源方向有关，与观测角度v无关，也就是从任何角度看同一个表面，看到的颜色都是相同的。

2.2.2高光反射

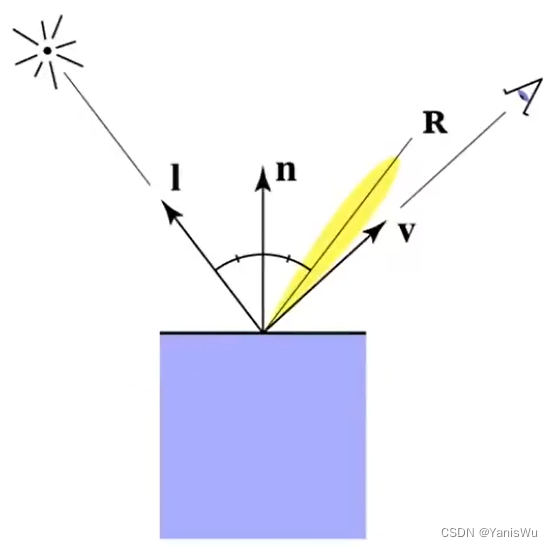
        如上图，假设物体表面非常光滑，那么光线照射的到物体表面会反射出去，上图中R表示反射光线，为镜面反射方向。这时从v方向望去，在R附近一定的范围内(黄色部分)，会有大量的光线射入眼睛，这时会观察到物体表面的高光。也就是v方向与镜面反射方向足够接近的时候，会产生高光反射，这个模型被称为Phong模型。

        后来人们发现判断视线v与反射光线R是否接近，可以用视线v和光源i的半程向量h与表面法线n是否接近来替代，这就是大名鼎鼎的Blinn-Phong模型，它也是经验模型。

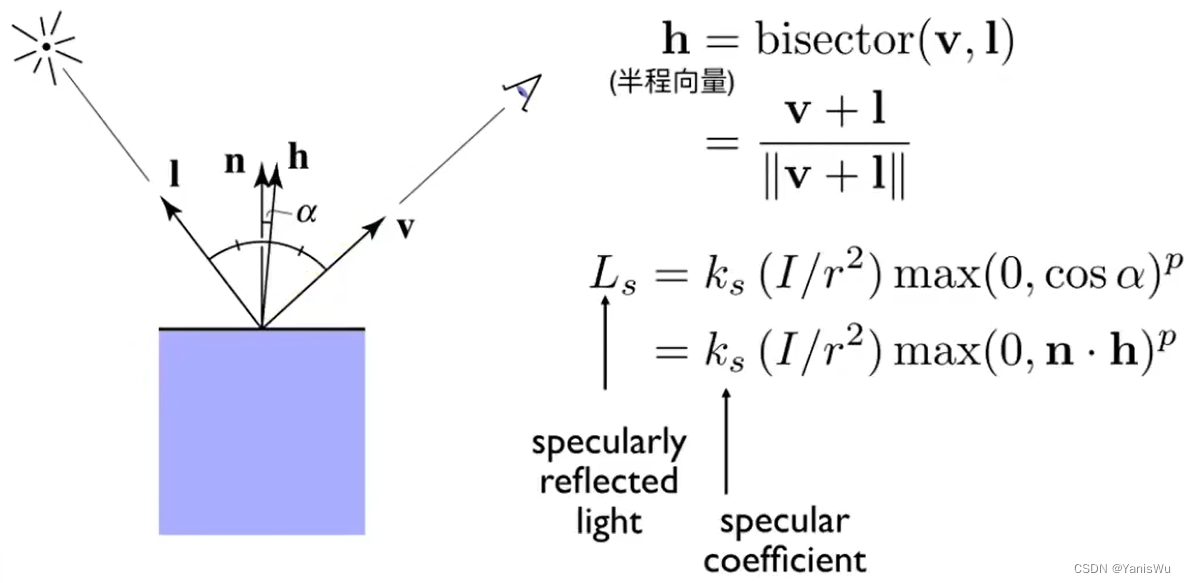
       如上图所示，求半程向量h非常简单，只需要将v与i相加，这就是为什么用Blinn-Phong模型，因为比Phong模型的R好算。

        为了判断h和n是否接近使用向量点乘，点乘结果越接近1表示两个向量越近，越接近0表示越远。

        与之前的漫反射计算不同的是计算高光反射时进行p次幂计算呢，现实中物体表面高光通常会比较小，这个p次幂是为了加速高光衰减，使其在较小的角度内就衰减完。如下图所示：

        用余弦夹角可以来判断两个向量是否接近，但是容忍度太低了。如上图最左边所示，就算在45度也是一个比较大的值，也就是有还有很高的高光，而现实世界中的高光一般是一个很小非常亮的一个点，也就是能看到高光的夹角非常小，于是给它进行次幂运算，发现64次幂时，大约20度左右就可以衰减到0。在Blinn-Phong模型中指数p通常会取100到200之间的数。

        计算高光参数与渲染结果的关系如下图所示：

        Ks表示镜面反射系数，从上到下，随着系数的增大，高光不断变量，来控制高光的亮度。
        从左到右随着指数p不断增长，看到高光的范围越来越小，也就是上文提到的通过指数来加速高光的衰减速度，使高光看起来更符合现实物体的高光。

2.2.3环境光

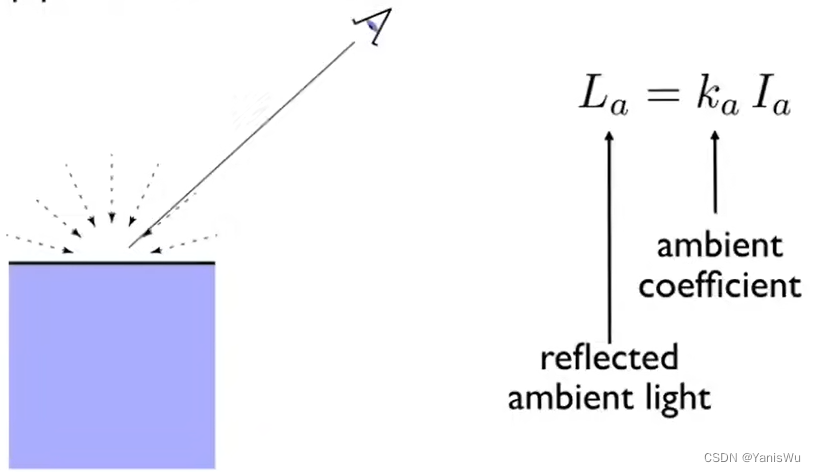
        在真实场景中，有些地方没有光源直接照射，但是通过光的反射到四面八方，所以这些地方间接的接收到了光。但是这个间接光是个很复杂的过程(全局光照)，所以就假设一个恒定的环境光来模拟，用Ia来表示环境光照强度，Ka表示环境光的系数或颜色。

        环境光与直接光照的方向l无关，与观测方向v和表面法线向量n也无关，所以环境光是一个常数，也就是某一种颜色。所以环境光的作用是为了保证没有地方完全是黑的，提升一个亮度。

2.2.4Blinn-Phong模型使用

        如上图，一个物体将它的环境光、漫反射、高光依据模型计算后累加，可以获得非常不错的渲染效果，使用这种方式计算材质的模型叫作Blinn-Phong反射模型。

        着色模型是考虑任何一个点(Shading point)长什么样，那么下一步自然是对所有的点进行着色操作，那整个场景就能看到了。

2.3着色频率

       如下图所示，三个球拥有完全相同的几何形状，为什么使用同一种着色后结果各不相同呢？因为着色频率(Shading Frequencies)不同。

        所谓着色频率，就是把着色运用到哪些点上。如果着色应用到每个面上，就是面着色(Flat Shading)，如上图第一个球所示。

        如果着色应用到每个面的顶点上，就是顶点着色(Gouraud Shading)，如上图第二个球所示。

        如果着色应用到每个像素上，就是片元(像素)着色(Phong Shading)，如图上第三个球所示。

2.3.1面着色

        以物体的表面为单位进行着色计算，由于每个面只有一个法线，所以同一个面有相同的光照效果。一个面的法线比较好获取，取任意两个边做个叉乘得到的结果就是法线。面着色每个面着色一次，所以着色效果较差。

2.3.2顶点着色

        在每个顶点上进行一次着色，每个顶点有自己的法线，三角形内部通过插值的方法获得对应位置的法线。一般来说，顶点着色效果比面着色较好。

如何计算顶点法线

        我们已经知道三角面的法线可以通过三角面上任意两边叉乘得到。如下图所示，已知围绕顶点v的四个面的法线，要想获得顶点v的法线，思路是将共用该顶点四个面法向求和取平均值即 Nv = (N1+N2+N3+N4)/4。

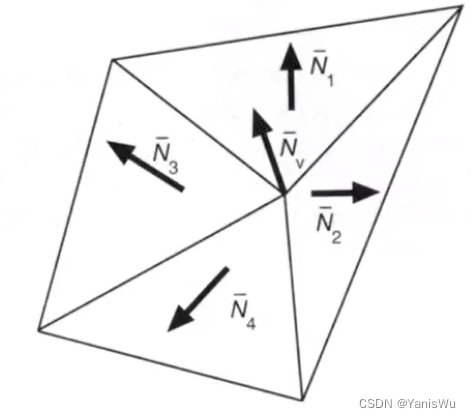
        但是这种实用与周边三角形面积差异不大的情况，如果其中一个三角形面积特别大还有一个面积特别小，简单的求平均值算出来的法线无法准确描述这个顶点的法线，这时就需要通过加权平均来获得更真实的结果，这里加权平均的权就是对应三角形的面积。

        我们知道两个向量叉乘得到这两个向量组成的平面的法线，同时该法线的长度等于原向量合成的平行四边形的面积。

        三角形的面积是平行四边形的一半，即所求三角形的法线的长度的一半为该三角形的面积。

2.3.3片元(像素)着色

        片元着色就是针对每个像素进行一次着色计算，会发现计算的高光更加圆润真实。但计算量也会更大。

        每一个像素的法线同样通过插值计算得到。如下图所示，假设已经知道了左右两个顶点的法线，那么中间每个像素的法线可通过两个顶点法线的插值得到。因为法线表示的是一个方向，所以计算后要记得归一化(调用normalize函数)变成单位向量。

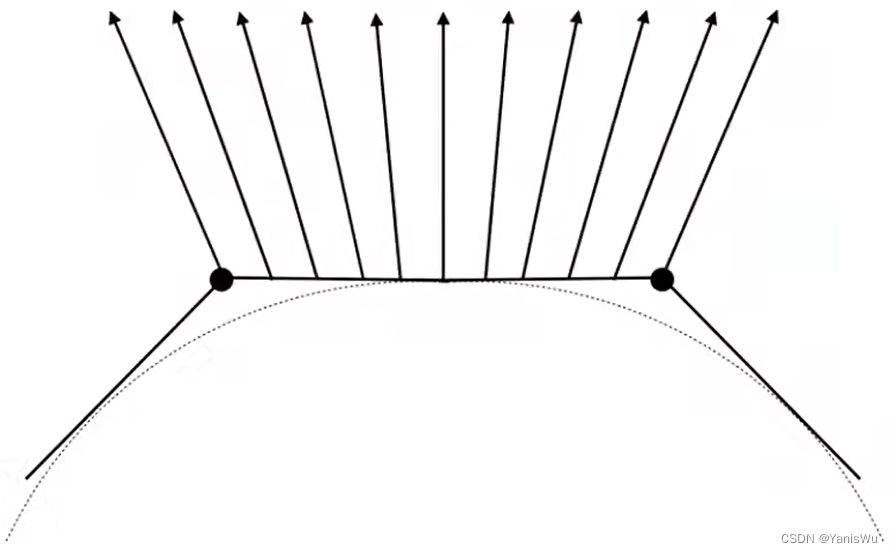
        那么怎么样插值出中间的法线呢？这里就要用到重心坐标的方式。

2.3.4三种着色频率区别

        三种着色频率的区别也是取决于不同模型，也不能说面着色效果就一定是最差的。如上图所示，从上到小，球模型的几何形态更加光滑，三角型面数更多。可以发现，当几何足够复杂的情况下，面着色也能渲染出很好的效果，但是计算量也会增加。所以说，选择什么着色频率(方式)，应综合考虑几何体的顶点数、想要达到的效果以及计算性能来决定。