一个正整数 N 的因子中可能存在若干连续的数字。例如 630 可以分解为 3×5×6×7，其中 5、6、7 就是 3 个连续的数字。给定任一正整数 N，要求编写程序求出最长连续因子的个数，并输出最小的连续因子序列。

输入格式：

输入在一行中给出一个正整数 N（1<N<231）。

输出格式：

首先在第 1 行输出最长连续因子的个数；然后在第 2 行中按 因子1*因子2*……*因子k 的格式输出最小的连续因子序列，其中因子按递增顺序输出，1 不算在内。

输入样例：

630

输出样例：

3
5*6*7

L1-006 连续因子_星河欲转。的博客-CSDN博客

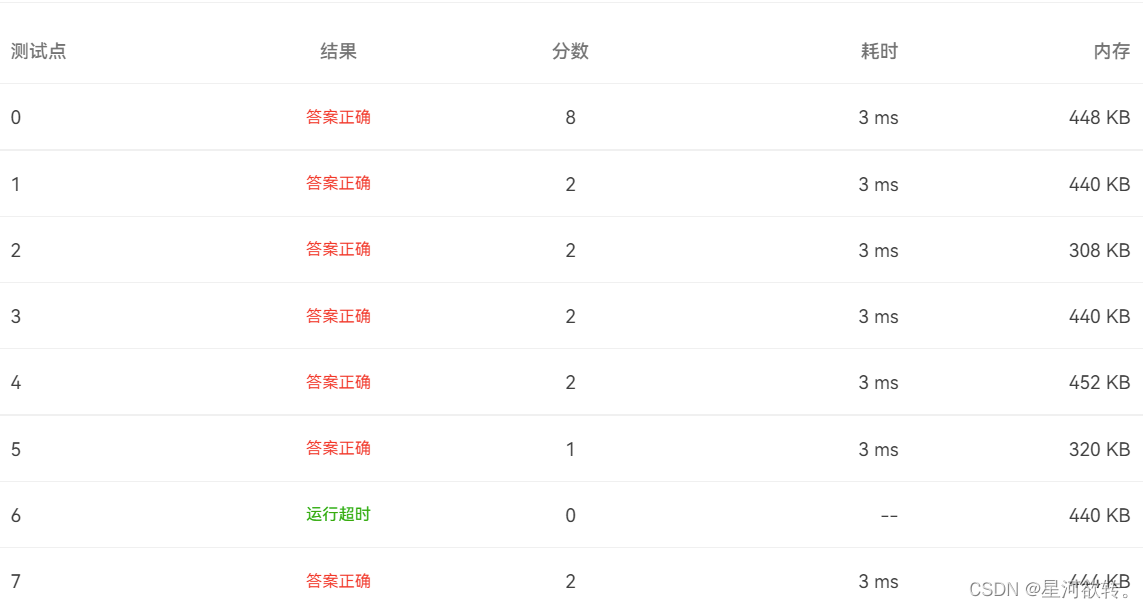
//真的是服了这个老六，以前做这道题刚开始是满分，后面增加了一个测试点之后变成19，好不容易找到了那个测试点，现在测试点又进行了改变，变成了超时。

//本人的代码相对之前没有太大变化，只是题目测试点有所改动，但是从题意上来说，本人这个更易理解。

我们要求的是最长的连续因子，记住，最长and连续and因子，同长的话取最小，不过这个不用考虑，因为我们就是从小到大开始的，x作用为记录我们所求连续因子的第一个，d记录长度，方便后面进行长度比较，a来记录连续因子乘积。

代码解析：我们令x=n，如果d等于0，输出1和n（也就是x），然后我们寻找能被n的因子，又从该因子开始，进行累乘，如果累乘结果不是n的因子或者超过了n，那么跳出这层循环，接着判断，从刚才跳出的位置减去开始的位置的这个长度是否大于之前的长度，大于则替换长度d值和起始因子x，如果d不为0，那就输出d和x，又从x的下一个位置输出，直到长度满足d。

第二个循环目的就是取连续因子，从前面第一个循环判断是因子那个位置开始进行连乘，再继续判断这个结果又是否是n的因子，然后又不断判断更新d和x。

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,x,i,j,d=0,a=1;
    cin>>n;
    x=n;
    for(i=2;i<=n/2;i++){
        if(n%i)continue;
        a=1;
        for(j=i;j<=n/2;j++){
            a*=j;
            if(n%a||a>n)break;
        }
        if(j-i>d){
            d=j-i;
            x=i;
        }
    }
    if(d==0)cout<<"1\n"<<x;
    else cout<<d<<endl<<x;
    for(i=x+1;i<x+d;i++)cout<<"*"<<i;
    return 0;
}

 //下面是学弟的满分代码,主要区别在于第二个循环.

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int n;

    cin >> n;

    int ans1 = 0, ans2;

    for (int i = 2; i <= sqrt(n); i ++){
        int temp = n;
        int x = i;
        int len = 0;
        while (temp % x == 0 and temp != 0){
            len ++;
            temp /= x;
            x ++;
        }
        if (len > ans1){
            ans1 = len;
            ans2 = i;
        }
    }

    if (ans1 == 0){
        cout << 1 << endl << n << endl;
    }else {
        int o = 0;
        cout << ans1 << endl;
        for (int i = ans2; i < ans2 + ans1; i ++){
            if (o ++) cout << '*';
            cout << i;
        }
    }
    
    return 0;
}