源自:系统工程与电子技术
作者:张杰 刘开蓉 陈金宝 张迎雪 陈传志 余虹志 张云啸
注:若出现无法显示完全的情况,可 V 搜索“人工智能技术与咨询”查看完整文章
摘 要
针对3维空间对抗环境下, 具有非线性二阶积分器动力学模型的多智能体系统(multi-agents system, MAS)时变编队机动与队形变换控制问题, 提出一种可抑制外部干扰的MAS时变编队机动与队形变换策略。首先, 根据空间对抗环境分析常见编队队形的效用, 设计一种基于应力矩阵和领导-跟随策略的24机编队立体构型, 通过灵活地仿射变换队形, 提高MAS编队空间对抗效率。其次, 基于一致性理论、滑模理论和鲁棒性控制, 利用时变编队应力矩阵, 设计了一种鲁棒一致性跟踪控制器, 以在外部未知扰动条件下, 确保MAS时变编队在机动与仿射变换时跟随者对领导者的精确协同跟踪。然后, 通过构造Lyapunov函数证明了外界未知扰动下3维MAS时变编队连续机动和队形变换的稳定性。最后, 通过仿真实验验证了所提出的控制器能够使时变编队在机动和队形变换过程中实现精确协同跟踪。
关键词
多智能体系统, 空间对抗, 编队队形控制, 应力矩阵
引言
多智能体系统(multi-agents system, MAS)在复杂空间对抗环境下交互作战是一种新型作战模式, 是根据自然界鸟群、蜂群、蚁群等群居动物生物种群的交流合作方式而诞生的[1]。相较于传统空间对抗载体, 大规模、低成本的MAS可利用内部拓扑网络实现协同侦察、协同打击、协同干扰等功能, 可被有效应用于反恐维稳、远程突防、战机护航等作战任务[2]。合适的MAS的集群化载荷部署还可以增强空间生存和打击能力, 扩大信息获取范围, 缩短复杂空间任务的完成周期, 是地-空-天联合体系的重要平台[3]。
协同控制是MAS时变编队控制的重要研究内容。按照协同控制策略, 协同编队可以分成基于领航-跟随控制编队、基于虚拟结构控制编队、基于行为控制编队、一致性控制编队、人工势场控制编队。随着控制方法的发展深入, 针对MAS时变编队队形保持、变换与避障等问题, 将上述研究策略和各类先进智能控制方法混合使用效果更佳。基于领航-跟随框架, 更容易应用复杂的控制算法, 例如动态逆控制[4-6]、滑模控制[7-8]、自适应控制[9-11]、模型预测控制[12-15]和模糊控制[16-19]等。
近年来, 基于图论的刚性理论分布式编队控制方法[20]被广泛研究。Lin等[21]将图论拉普拉斯矩阵的交互权重由正实数拓展到实数, 形成仿射队形, 该方法也被称为仿射编队控制。Wang等[22]将仿射编队控制的拓扑图由无向图延伸到有向图。文献[23]完整总结了无向图和有向图的仿射控制充分必要条件。
针对3维甚至更高维度的MAS时变编队控制策略已有诸多成果。Kwon等[24]将Park等[25]提出的弱刚性概念拓展到3维空间的三角形编队。Tang等[26]基于方位和相对速度解决了3维空间中的编队控制问题, 并用4个智能体的仿真实验验证了该方法的有效性。Zhao等[27]探究了轴承刚度理论, 提出适用于任意维度空间的基于方位的分布式编队控制策略, 并用8个智能体组成的立方体验证该方法。随后, Xu等[28]实现了用任意积分动力学控制跟随者, 成功跟踪领导者在任意维度上的任意阶多项式轨迹, 并分别用由9个智能体组成的立方体编队和由10个智能体组成的平面楔形编队验证该策略。上述文献中研究的MAS时变编队大多是由3~10个智能体组成的3维编队, 且编队队形简单, 没有考虑外部干扰, 对于实际空间对抗任务需求, 算法应用依旧比较困难。
本文针对3维空间对抗环境中的大型MAS时变编队机动与队形变换稳定控制问题, 设计了一种大型MAS编队立体矩形基础构型, 并提出一种可有效抑制外部未知扰动的MAS时变编队的鲁棒一致性跟踪控制器。与现有研究成果相比, 本文工作的创新性体现如下:
(1) 基于空间对抗环境, 分析了一字形、楔形、菱形等常规编队队形的对抗效用, 设计了一种基于应力矩阵和领航-跟随控制策略的3维24机编队立体矩形构型, 其可通过灵活仿射变换为一字形、菱形等其他队形, 从而达到多种队形的对抗与避障效果, 提高对抗效能;
(2) 为实现24机立体构型编队在机动与队形变换中的稳定控制, 考虑外界未知扰动情况, 基于一致性理论、滑模理论和鲁棒性控制, 设计了MAS时变编队跟随者的鲁棒一致性跟踪控制器。该控制器可有效抑制外界未知扰动, 消除跟踪过程误差, 解决领航-跟随时变编队协同控制中的跟随者跟踪控制问题。
1 预备知识
图论是分布式控制和一致性理论的基础[29]。在一致性理论中, 拉普拉斯矩阵十分重要, 其具有许多重要性质[30], 尤其是半正定性对于控制系统稳定性证明十分重要。
1.1 无向图
作为MAS通信拓扑工具, 严格来说, 各类图的强度效果根据“有向图<强连接图<生成树<平衡图<无向图”逐渐加强[31]。无向图G=(V, E)由n个节点集V={V1, V2, …, Vn}和边集E={(i, j): i, j∈V, i≠j}组成的拓扑通信网络, 用于描述智能体之间的相互作用。其中, Vi表示智能体i, 边(i, j)∈E或(j, i)∈E表示Vj∈V和Vi∈V是彼此的邻居。对于智能体i, 所有可访问智能体的集合表示为Ni, 也称为i的邻居集, 即Ni={Vi|(i, j)∈E}, Ni是智能体i的邻居数量。无向图G的邻接矩阵为A=[aij]∈Rn×n, 其中若(i, j)∈E, 则(j, i)∈E也存在, 且aij=aji=1, 否则为0。
考虑在欧几里得空间Rd中的一组n个智能体, 其中d≥3, n≥d+1。设pi∈Rd是智能体i的位置, 则p=[p1T,p2T, …,pnT]T∈Rd是所有智能体的配置矩阵。在不失一般性的情况下, 假设前nl个智能体是领导者, 剩余的智能体则为跟随者nf=n-nl, 则领导者和跟随者分别为Vl={1, 2, …, nl}, Vf=V/ Vl。领导者和跟随者的位置分别表示为pl=[p1T,p2T, …,pnlT]T和pf=[pnl+1T,pnl+2T, …,pnT]T。将无向图G及其相应的配置矩阵P=[pl,pf]置于Rd中, 从而获得编队(G, P)。
1.2 仿射空间
编队的配置矩阵P∈Rn×d和增广矩阵 P∈Rn×(d+1)为
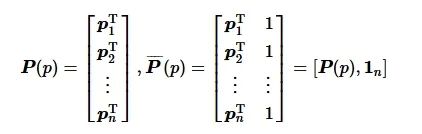
(1)
式中:
![]()
。
引理1 仿射空间的秩条件[32]。当且仅当n≥d+1时, 点集{pi}i=1n仿射空间为Rd且rank(P(p))=d+1。
定义一个非奇异矩阵A=Rd×d表示队形伸缩、旋转等变换, 位移向量b∈Rd表示在上述变换之上进行位置偏移, 均在时间t上连续。标称配置矩阵r代表所需要保持的集群队形, 智能体i∈V在目标编队中的理想位置为
![]()
(2)
其中,
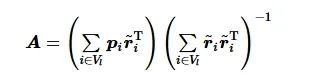
(3)
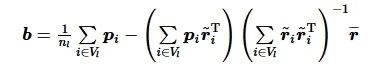
(4)
且
![]()
。
MAS时变编队协同控制的目的可以表达为:
![]()
。
1.3 应力矩阵
应力矩阵又称为符号拉普拉斯矩阵, 与拉普拉斯矩阵类似, 均表述了个体之间的通信拓扑关系, 不同之处在于应力矩阵包含了个体与邻居的位置关系, 表征的是一个构型或者图的内部力平衡状态。
在数学和力学理论与应用中, 参数ωij是图G的边(i, j)上的一个标量权重, 建模了智能体之间的拓扑信息流结构, 且ωij=ωji成立。当ωij>0时, 表示边(i, j)存在引力, 反之则为斥力。向量ωij(pj-pi)表示智能体 j 通过边(i, j)施加在智能体 i上的力。对于一个编队(G, P), 若能满足下述要求
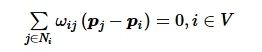
(5)
则称ω为配置矩阵P的平衡应力。因此, 式(5)意味着由智能体j∈Ni施加在智能体i上的力是平衡的。将ω=(ω1, ω2, …, ωm)T∈Rm表示应力向量, 其中ωk对应于第k个无向边, k=1, 2, …, m。
值得注意的是, 平衡应力只能在标量因子的范围内确定, 即若ω是平衡应力向量, 那么对于任何k∈R≠0, kω也是平衡应力向量。将式(5)写为矩阵形式, 即为
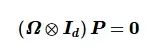
(6)
应力矩阵
![]()
定义如下:
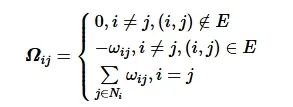
(7)
应力矩阵的性质与编队结构的通用刚性密切相关。下面给出需要用到的两个关于应力矩阵的引理, 分别用于建立应力矩阵与结构为通用刚性、仿射映像的关系。
引理2 仿射编队通用刚性条件[33]。给定一个具有n个节点的无向图G和通用配置矩阵P, 且n≥d+2。当且仅当存在一个应力矩阵Ω,Ω是半正定的, 且rank(Ω)=n-d-1, 则编队(G, P)是通用刚性的。
引理3 仿射可定位的应力条件[33]。当且仅当领导者的标称配置
![]()
仿射空间为Rd, 同时具有半正定应力矩阵Ω且rank(Ω)=n-d-1, 当且仅当增广应力矩阵 Ωff模块是非奇异时, 标称编队(G, r)是仿射可定位的,pf可以被唯一确定, 且pf=- Ωff-1Ωflpl。根据领导者和跟随者将增广应力矩阵分解为
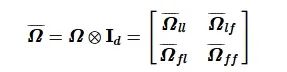
(8)
式中:
![]()
。
进一步定义跟随者跟踪误差和速度误差为
![]()
(9)
![]()
(10)
假设1 编队可仿射变换的条件。假设MAS时变编队领导者数目n>d+1且有半正定应力矩阵Ω, rank(Ω)=n-d-1。
注1 基于图论、应力矩阵、全局刚性、仿射空间的引理1、引理2表述集群编队的队形结构, 以及通信拓扑需满足的要求, 是引理3的前置条件。基于仿射定义与仿射可定位的引理3, 给出了集群编队的期望信息, 可由领导者位置求解跟随者位置, 通过领导者位置与队形配置信息确定整体队形变换。
2 大型空间对抗编队队形设计
从有人机长期作战经验可了解到, 合理有效的空间对抗MAS队形可以充分发挥空中兵力的整体威力, 提高协同作战效率, 满足获取战场态势信息的及时性、增加编队飞行的安全性和隐身性、提高任务完成率等任务要求。常用的空间对抗编队队形有“一”字形、楔形、菱形等多种队形[34]。
“一”字形编队可分为平行编队与纵向编队, MAS间距根据智能体的侦查设备载荷的搜索能力、航行安全距离来调整。如图 1所示, 在平行编队队形中, 智能体横向一字排开, 主要用于大面积搜索目标, 智能体数量的增加可以明显扩大搜索范围, 提高作战效率。纵向编队主要用于躲避障碍物、轰炸地面目标等任务, 当编队在没有对方威胁的区域航行时, 编队领导者可以带领编队航行, 穿越、躲避空间障碍物。
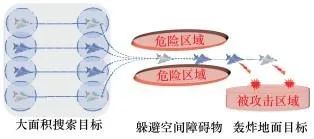
图1 “一”字形编队
楔形紧密编队主要用于出航和返航, 编队最前方为领航机, 有利于MAS减小燃油消耗, 增大航程。菱形编队主要用于攻击, 有利于提高攻击效率, 增加完成任务的概率。处于前方的智能体攻击目标之后对攻击效果进行评估, 如果需要二次攻击, 处于斜后方的智能体可以执行二次攻击, 否则斜后方的智能体可以继续执行其他任务。这样, 前方的智能体无需掉头进行二次攻击, 从而节省智能体能量消耗。MAS编队领导者可以处于编队的后方安全区域, 并且实时监督每颗智能体的飞行状态和任务执行情况, 必要时可直接修改智能体作战任务。
菱形编队还可实现保护MAS领导者安全的效果。当编队遭遇强于自身的空间力量袭击时, MAS跟随者在领导者周围保护领导者迅速撤离战场, 跟随者吸引敌方来袭, 必要时以机身来阻挡来袭袭击, 以最大限度地保护领导者。编队功能如图 2所示。
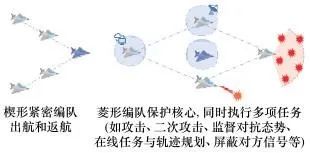
图2 楔形紧密编队和菱形编队
矩形编队分为大纵深的队列布阵和浅纵深宽横面的方阵。相比于适用于扩大拦截面积的浅纵深宽横面方阵, 大纵深队列布阵更适合执行协同任务, 火力载荷装备在前排智能体上, 光学探测或其他重要载荷装备在前排阵后, 横排数量少, 可以有效提高航行、对抗及应战速度。
相较于其他队形(如楔形、圆形等)作为仿射变换基础队形的单一效果, 基于矩形的仿射变换可变换为“一”字形、菱形, 可达到楔形队形的巡航和轰炸、圆形队形的围攻和信号屏蔽等队形的作战效果, 如图 3所示。基于此, 本文选用矩形编队为空间对抗的MAS基础队形。
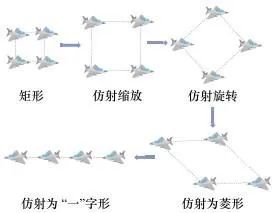
图3 矩形编队仿射变换
3 MAS时变编队跟踪控制器设计
3.1 问题描述
假定在欧几里得空间R3中, 所有智能体考虑如下二阶积分器动力学模型:
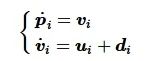
(11)
式中:pi是智能体的位置;vi为智能体的速度;ui是所需设计的控制输入;di是外界扰动。
假设2 编队领导者的轨迹保持。领导者轨迹提前由智能轨迹规划器生成, 且其时刻位于目标编队位置内, 即对于任意时刻t, 均有
![]()
。
3.2 无扰动的跟随者一致性跟踪控制器设计
考虑MAS动力学模型为式(11), 当di≡0 时, 基于假设1、假设2, 对每个跟随者i∈Vf 设计如下一致性跟踪控制器:
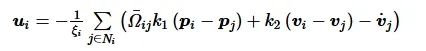
(12)
式中:k1、k2是正常数的控制增益;
![]()
, 由于 Ωff是正定矩阵, ξi≥0恒成立。
定理1 考虑MAS动力学模型为式(11), 基于假设1与假设2, 式(12)跟随者一致性跟踪控制器可使时变编队在无外界扰动下, 形成并维持期望的仿射变换队形, 且机动过程中跟随者位置误差||δpf(t)||和速度误差||δvf(t)||全局指数地快速收敛至零。
证明 根据式(12)有
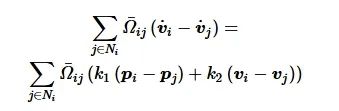
(13)
将式(13)写为矩阵-向量形式:
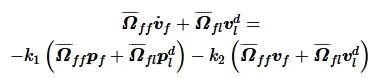
(14)
其中,定义
![]()
。
化简式(14)可得:
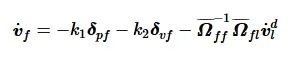
(15)
由于 Ωff是非奇异的, 将式(15)代入式(10)得
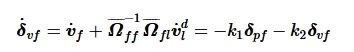
(16)
将式(16)写为矩阵-向量形式:
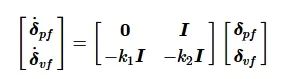
(17)
式(17)也为误差动力学, 其状态矩阵的特征值为
![]()
, 对于任何k1、k2, 它总是具有负实部, 具有渐进稳定性。
定义
![]()
, 且S是包含控制增益k1、k2的状态矩阵。当且仅当S是Hurwitz时,φ可以收敛至零, 从而推断出k1、k2是正常数。证毕
3.3 存在未知扰动的跟随者鲁棒一致性跟踪控制器设计
考虑MAS动力学模型为式(11), 当di 不为零时, 在式(12) 控制器基础上, 对di 采用扰动估计, 从而进行扰动补偿。
假设3 外界扰动有界性。外界未知扰动di是有界的, 且存在常数dmax≥0使得||di||≤dmax。
假设4 扰动估计有界性。令
![]()
是扰动估计器对外界未知扰动di 的估计值, 存在扰动估计器使得
![]()
是有界的, 且
![]()
。
基于假设3与假设4, 考虑对每个跟随者i∈Vf设计如下鲁棒一致性跟踪滑模控制器:
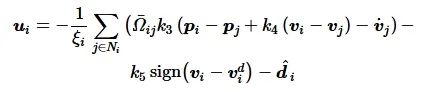
(18)
式中:k3,k4,k5是正常数的控制增益;
![]()
, 由于 Ωff是正定矩阵, ξi ≥0恒成立,
![]()
是扰动di 估计值。
定理2 考虑MAS动力学模型为式(11), 基于假设3与假设4, 式(18)跟随者鲁棒一致性跟踪滑模控制器可使时变编队在外界未知扰动下, 能够形成并维持期望的仿射变换队形, 且机动过程中跟随者位置误差
![]()
全局指数地快速收敛至零。
证明 根据式(18)有
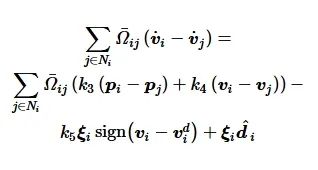
(19)
将式(19)写为矩阵-向量形式:
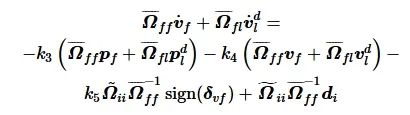
(20)
其中, 定义
![]()
。
化简式(20)可得:
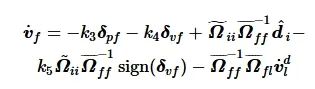
(21)
由于 Ωff是非奇异的, 将式(21)代入跟踪误差式(10)得
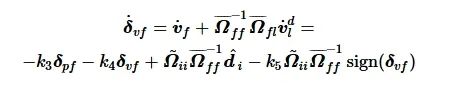
(22)
将式(22)写为矩阵-向量形式:
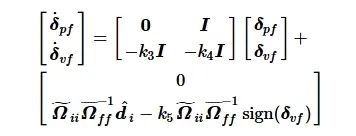
(23)
式(23)也称为误差动力学, 其状态矩阵的特征值为
![]()
, 对于任何k3、k4, 它总是具有负实部, 具有渐进稳定性。
定义
![]()
, 且S是包含控制增益k1、k2的状态矩阵。当且仅当S是Hurwitz时,φ可以收敛至零, 从而可推断出k3、k4是正常数。
构造Lyapunov函数如下:
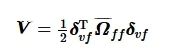
(24)
对式(24)求导得
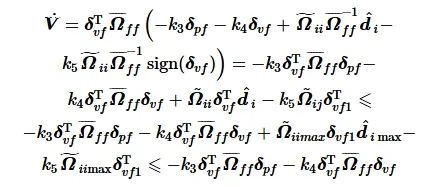
(25)
由式(19)可知, 当
![]()
成立, 即
![]()
。由Barbalat引理可得, 当t→∞时, 实现
![]()
。式(18)控制律使得MAS时变编队的跟随者跟踪领导者时变运动状态, 编队保持构型稳定。证毕
3.4 扰动估计器设计
考虑对跟随者i∈Vf 设计外界未知扰动估计器。令
![]()
的拉普拉斯表达式满足关系式:
![]()
(26)
其中Q为低通滤波器, 保证了系统正则性和可实现性。取Q拉氏变换为
![]()
(27)
令
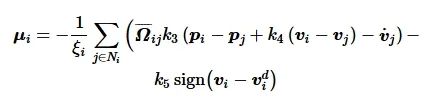
(28)
由式(26)、式(27)和式(28)得
![]()
(29)
从而得外界未知扰动估计值为
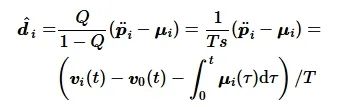
(30)
定理3 式(30)扰动估计器使得
![]()
是有界的, 且
![]()
。
证明 引入扰动估计误差
![]()
为
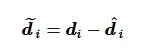
(31)
根据式(26)和式(31), 得
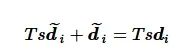
(32)
式(32)的时域表达式为
![]()
(33)
将式(33)视为输入为
![]()
, 状态为
![]()
的系统。当
![]()
成立时, 由于式(33)是全局输入状态稳定的, 显然可得
![]()
。且滤波器截止频率为T-1。具体证明推导过程与文献[35]过程类似, 在此不再赘述。
证毕
至此, 针对式(11)具有外部扰动的MAS模型, 本文提出了MAS时变编队跟随者的鲁棒一致性跟踪控制器式(18), 其控制结构如图 4所示。该控制器由两个部分组成: 一部分是基于应力矩阵的一致性滑模跟踪控制, 作为系统稳定器; 另一部分为外部扰动估计器, 可以有效抑制系统受到的外界未知扰动。
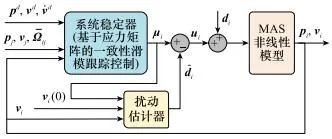
图4 MAS时变编队跟随者的鲁棒一致性跟踪算法
4 仿真与分析
4.1 标称队形和标称配置矩阵设计
为了实现所提出的MAS时变编队跟随者鲁棒一致性跟踪控制器式(18), 需要设计满足引理3与假设1条件的标称编队队形。在3维空间内至少需要4个领导者, 基于领航-跟随策略, 设计了4×3×2阵列的24机MAS时变编队为标称编队, 给定对应的配置矩阵P(r)∈ R24×3和邻接矩阵A=R24×24。编队构型如图 5所示, 图中红色标记为领导者, 蓝色标记为跟随者, 黑色连接线代表智能体间的邻接通信拓扑关系。该MAS时变编队领导者数量满足4≥d+1=3+1, 而且领导者的位置并不共面, 对应的无向图也是4根的。
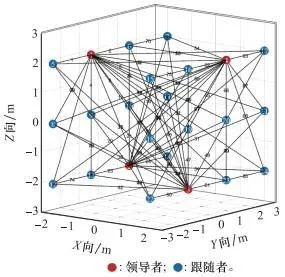
图5 24机智能体的标称编队
24机编队标称配置矩阵P(r)为
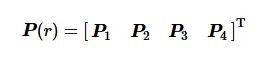
(34)
其中,

24机编队邻接矩阵A可由图 5得出。
4.2 应力矩阵计算
根据本文应力矩阵分析与刚性集群要求, 应力矩阵应满足引理2、引理3。Zhao等[32]提出一种用于构造普遍刚性框架的正半定应力矩阵的算法。该构造方法基于矩阵奇异值分解(singular value decomposition, SVD)和乘法逆特征值(multiplicative inverse eigenvalues, MIE)算法, 其中需要无向图的配置矩阵全局信息。但其所提出的基于应力矩阵的编队控制器是完全分布式的, 不需要全局信息, 与分布式控制文献中经常使用的控制设计策略“集中式设计, 分布式实现”一致[36]。
根据Zhao等[32]的应力矩阵求解算法, 通过配置矩阵与邻接矩阵解算即可得到24机编队的应力矩阵Ω。
注2 一个MAS编队的应力矩阵可视为符号拉普拉斯图, 其结构由无向图G确定, 但应力矩阵元素的值由编队构型(即标称配置矩阵和邻接矩阵)共同确定。由于一个MAS编队构型的标称配置矩阵、邻接矩阵具有多解, 因此其应力矩阵通常是不确定的。
4.3 MAS时变编队机动与仿射变换仿真实验
在仿真实验中, MAS选用模型式(11), 领导者智能体以时变且连续的理想加速度进行预设轨迹运动, 式(18)作为MAS时变编队跟随者的鲁棒一致性跟踪滑模控制器, 外界干扰di(t)=5sin(100t), 并赋予MAS时变编队初始位置随机位置误差。
实验得到24机MAS时变编队机动与仿射变换轨迹如图 6和图 7所示, 红色标记的为4个领导者, 蓝色标记的为20个跟随者。t=0 s时标称队形位置具有随机位置误差; t=6 s前迅速恢复至标称队形位置并起飞; t=17 s和t=39 s时连续仿射放大队形通过大型障碍; t=62 s时仿射缩小, 队形渡过障碍; t=75 s时由矩形立体构型仿射为矩形2维平面, 可用于屏蔽信号、围攻; t=118 s时矩形2维平面旋转渡过狭长障碍; t=179 s时矩形2维平面仿射变换为一字形队形渡过狭小障碍, 该队形也可用于自杀式攻击; t=179 s时由一字形队形仿射为矩形立体3维构型; t=269 s时整体旋转绕过危险区域; t=364 s时发现前下方为作战危险区域, 准备仿射变换为菱形队形作战; t=450 s时仿射变换为菱形队形, 扩展面积攻击下方危险区域, 也可用于攻击前方、保护核心智能体。
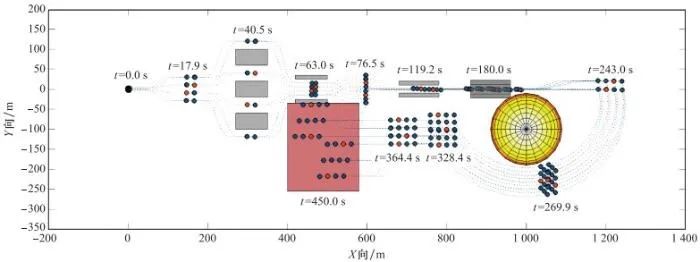
图6 时变扰动下MAS时变编队的鲁棒一致性跟踪控制仿真轨迹(X-Y平面视角)
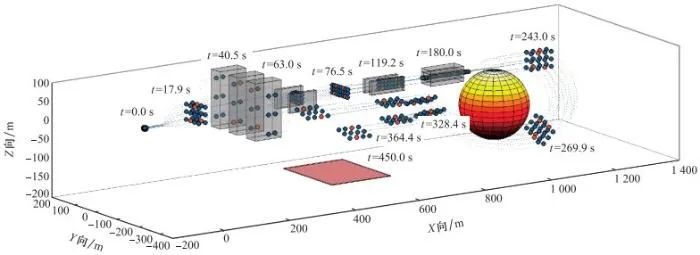
图7 时变扰动下MAS时变编队的鲁棒一致性跟踪控制仿真轨迹(3维视角)
24机MAS时变编队跟随者位置误差变化如图 8(a)所示, 可以看出跟随者位置跟踪误差的l2 范数能够快速收敛至零, 且在整个过程中基本保持在零附近。为了更清楚地对比扰动估计器的作用, 还针对式(18)进行了有无扰动估计器的对比实验, 无扰动估计器的位置跟踪误差变化如图 8(b)所示。
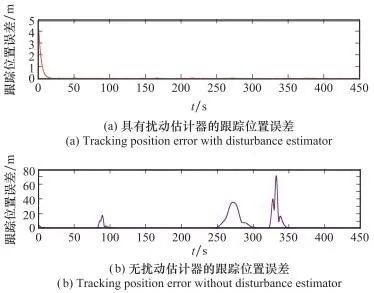
图8 时变扰动下MAS时变编队的跟随者位置跟踪误差
相应地, 24机MAS时变编队速度、加速度的变化如图 9和图 10所示, 从图中可以看出当产生机动时, 跟随者的速度和加速度没有产生明显的波动。
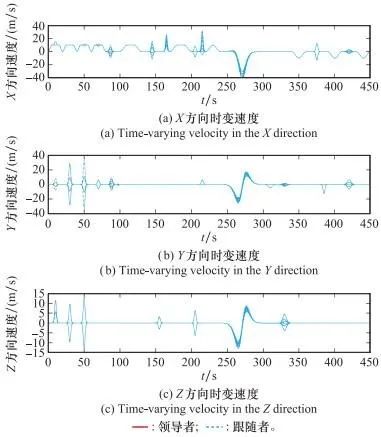
图9 时变扰动下MAS时变编队在X、Y和Z方向的速度变化
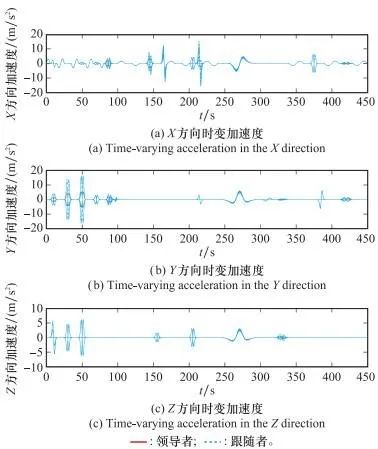
图10 时变扰动下MAS时变编队在X、Y和Z方向的加速度变化
从实验中可以看出, MAS时变编队的领导者智能体在机动过程中无须始终保持在空间内的仿射张成。机动过程中领导者编队会出现共线情况, 例如, 领导者编队连续机动合并为一字形、矩形平面、菱形编队, 但MAS时变编队的定位性和稳定性不会受到影响。本文所提出的鲁棒一致性跟踪滑模控制器能够实现MAS时变编队在不同方向上的连续平移、旋转、放缩, 且能够使得整个MAS时变编队在复杂空间对抗环境内增大攻击效能、拥有可变形避障功能。
5 结论
本文面向空间对抗环境设计了一种基于leader-foll-ower框架和应力矩阵的3维24机编队矩形立体构型, 提出一种可有效抑制外部扰动的MAS时变编队的鲁棒一致性跟踪控制器, 只需控制少量编队领导者, 即可实现整个编队的稳定机动与仿射变换。
仿真实验考虑了外界未知扰动、外界威胁和环境障碍规避等情况, 经过验证, 在本文提出的控制器作用下, 本文设计的24机编队可以快速消除外界未知扰动和机动过程误差, 执行直线飞行、旋转等机动动作, 灵活、稳定地仿射变换为具有对抗、保护、围攻、避障性能的其他队形, 从而只采用一个基础编队构型便能具有多种队形对抗效能, 适用于复杂任务作战情景, 为MAS编队作战提供了参考。
但是本文没有考虑智能体之间、智能体与环境之间的避碰, 未来可考虑进一步融合拟态物理学(artificial phy-sics, AP)算法, 使得MAS时变编队在更为复杂的空间对抗环境内进一步提升系统的环境自适应性与稳定性。
声明:公众号转载的文章及图片出于非商业性的教育和科研目的供大家参考和探讨,并不意味着支持其观点或证实其内容的真实性。版权归原作者所有,如转载稿涉及版权等问题,请立即联系我们删除。
注:若出现无法显示完全的情况,可 V 搜索“人工智能技术与咨询”查看完整文章