一、研究背景和意义
随着房地产市场的快速发展,房价数据成为了人们关注的焦点。了解房价的分布特征、影响因素以及不同区域之间的差异对于购房者、房地产开发商、政府部门等都具有重要的意义。通过对房价数据的聚类分析,可以深入了解房价的内在结构和规律,为相关决策提供科学依据。
研究意义:
- 为购房者提供参考:通过聚类分析,可以将房价数据分为不同的类别,购房者可以根据自己的需求和预算选择适合的房源。
- 帮助房地产开发商制定营销策略:了解不同区域的房价特征和需求,可以帮助房地产开发商制定更有针对性的营销策略,提高销售效率。
- 为政府部门提供决策支持:政府部门可以通过房价数据的聚类分析,了解房地产市场的发展趋势和存在的问题,制定相应的政策措施,促进房地产市场的健康发展。
- 推动房地产市场的研究:房价数据的聚类分析是房地产市场研究的重要内容之一,通过对房价数据的深入分析,可以推动房地产市场的研究不断深入。
二、实证分析
首先导入数据集基本的包
数据和代码
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt然后读取数据集和展示
# 读取文件
file_path = 'df_cleaned2.csv'
data = pd.read_csv(file_path, encoding='utf-8')
# 展示数据的前几行以了解结构
print(data.head())
随后查看数据类型

接下来查看缺失值的情况
# 查看缺失值情况
missing_values = data.isnull().sum()
missing_values
# 绘制缺失值情况的柱状图
# 绘制缺失值情况的柱状图
plt.bar(missing_values.index, missing_values.values, color=['black' if value == 0 else 'white' for value in missing_values.values])
plt.xlabel("变量")
plt.ylabel("缺失值数量")
plt.title("数据集缺失值情况")
plt.xticks(rotation=90)
plt.show()
从上面的结果和可视化可以发现该数据集没有缺失值,接下来进行统计学描述性分析
# 描述性分析
data.describe()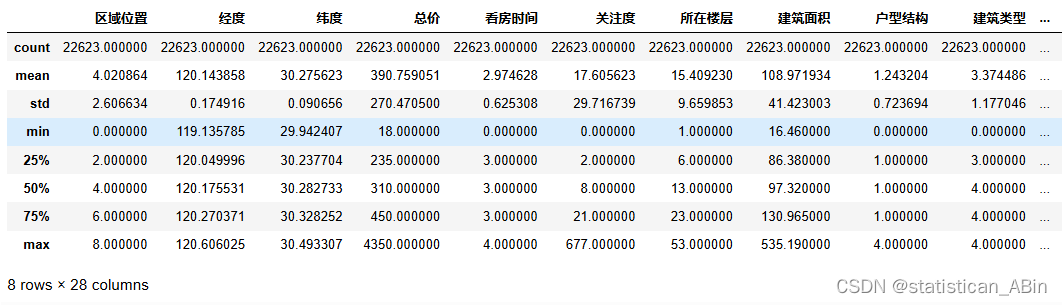
接下来进行特征可视化,首先进行房价直方图可视化
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif'] = ['KaiTi'] #中文
plt.rcParams['axes.unicode_minus'] = False #负号
# 可视化
# 绘制总价的直方图
plt.hist(data["总价"], bins=20,color='pink')
plt.xlabel("总价")
plt.ylabel("频数")
plt.title("总价分布直方图")
plt.show()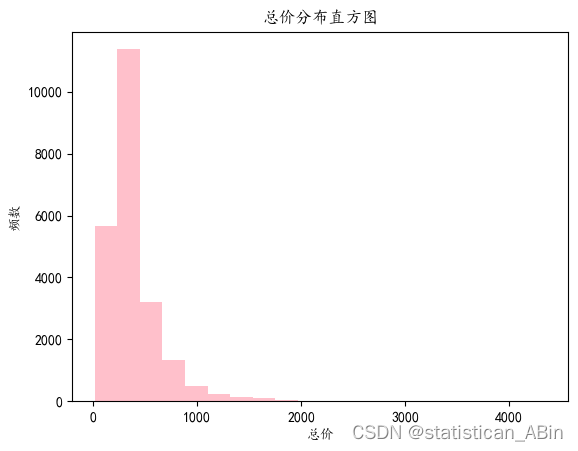
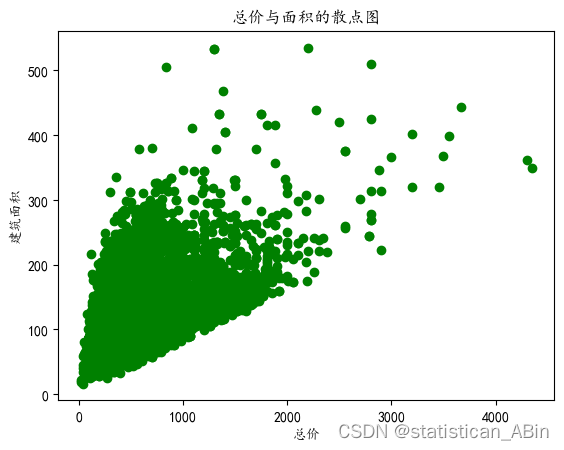
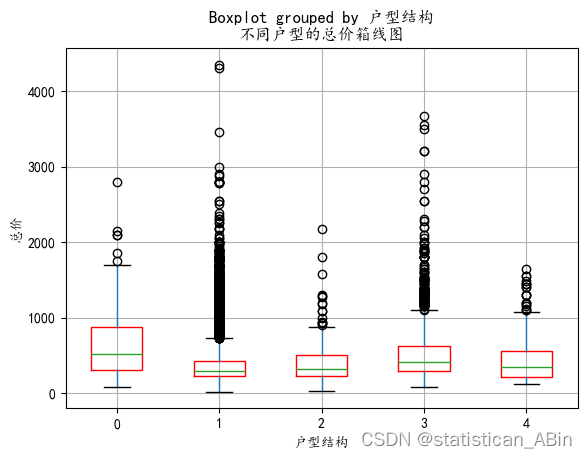
接下来进行区域分析
# 区域分析
data["区域位置"] = data["区域位置"].astype("category")
data.boxplot(column="总价", by="区域位置",boxprops={'color':'blue'})
plt.xlabel("区域")
plt.ylabel("总价")
plt.title("不同区域的总价箱线图")
plt.show() 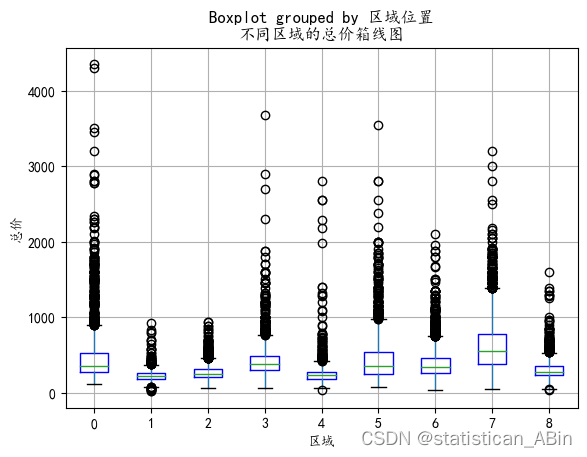
# 绘制不同户型的平均总价柱状图
data.groupby("户型结构")["总价"].mean().plot(kind="bar",color='orange')
plt.xlabel("户型")
plt.ylabel("平均总价")
plt.title("不同户型的平均总价柱状图")
plt.show()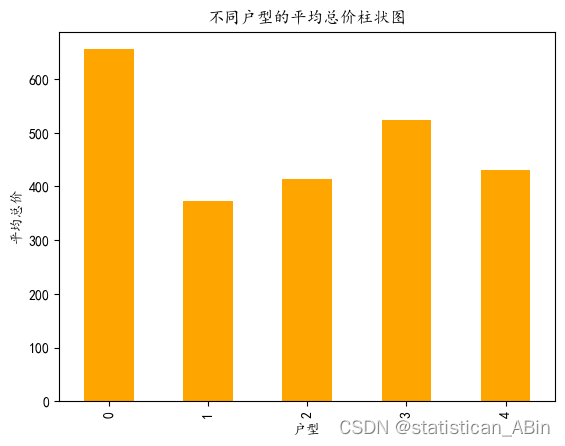
接下来计算特征直接的相关系数
correlation_matrix = data.corr()
correlation_matrix 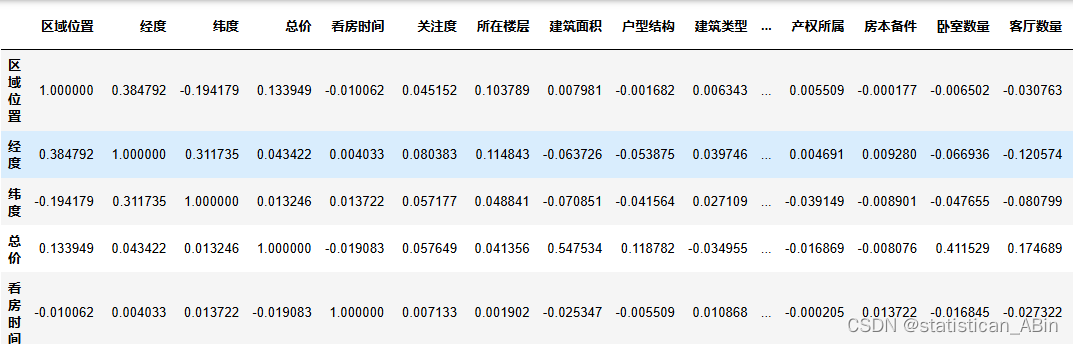
热力图:
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap="coolwarm")
plt.title("相关系数热力图")
plt.show()接下来进行聚类分析,首先进行特征选择,选择特征:关注度、总价、卫生间数量、建筑面积,然后标准化特征
随后使用手肘方法和轮廓系数确定最佳 K 值
sse = {}
silhouette_scores = {}
for k in range(2, 11): # 从 2 开始,因为轮廓系数至少需要 2 个簇
kmeans = KMeans(n_clusters=k, random_state=42).fit(scaled_selected_features)
sse[k] = kmeans.inertia_
silhouette_scores[k] = silhouette_score(scaled_selected_features, kmeans.labels_)
# 绘制手肘图
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(list(sse.keys()), list(sse.values()), marker='o')
plt.xlabel("Number of Clusters (K)")
plt.ylabel("SSE (Sum of Squared Errors)")
plt.title("Elbow Method for Determining Optimal K Value")
plt.grid(True)
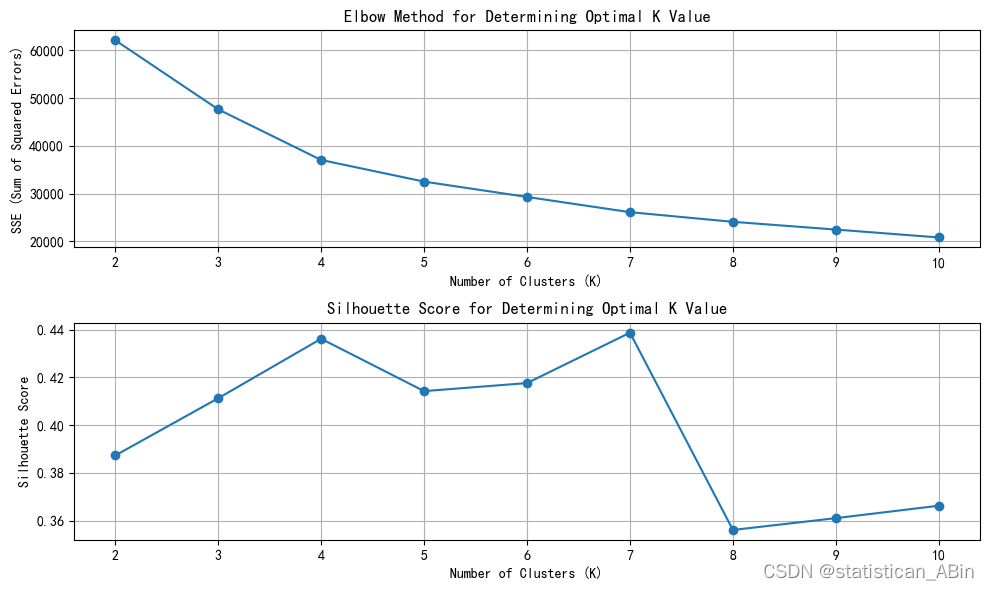
接下来使用 PCA 进行降维以便于可视化
pca = PCA(n_components=2) # 降至 2 维
pca_result = pca.fit_transform(scaled_selected_features)
# 可视化聚类结果
plt.figure(figsize=(10, 6))
plt.scatter(pca_result[:, 0], pca_result[:, 1], c=labels, cmap='viridis', marker='o')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title(f'K-means Clustering with K={k} (PCA Reduced)')
plt.grid(True)
plt.show()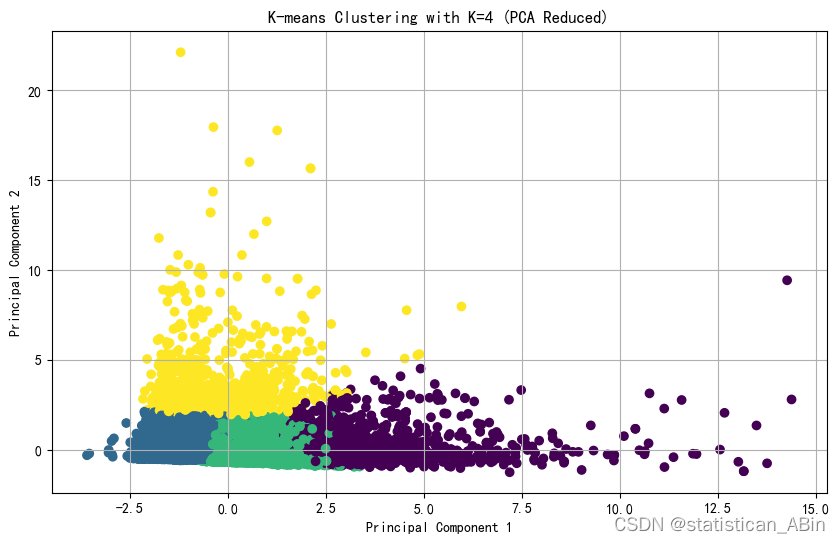
随后得出聚类中心
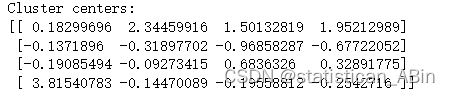
接下来根据聚类中心画出雷达图
# 标签,用于表示不同的聚类中心
labels = ['Cluster 1', 'Cluster 2', 'Cluster 3', 'Cluster 4']
# 特征数
num_features = len(centers[0])
angles = np.linspace(0, 2 * np.pi, num_features, endpoint=False).tolist()
# 将第一个特征点重复以闭合雷达图
centers = np.concatenate((centers, centers[:,[0]]), axis=1)
angles += angles[:1]
fig, ax = plt.subplots(figsize=(8, 8), subplot_kw=dict(polar=True))
ax.set_theta_offset(np.pi / 2)
ax.set_theta_direction(-1)
# 绘制雷达图
for i in range(len(centers)):
ax.plot(angles, centers[i], linewidth=2, label=labels[i])
ax.fill(angles, centers[i], alpha=0.25)
# 添加标题和图例
plt.title('Radar Chart of Clusters')
plt.legend(loc='upper right', bbox_to_anchor=(1.1, 1.1))
plt.show()
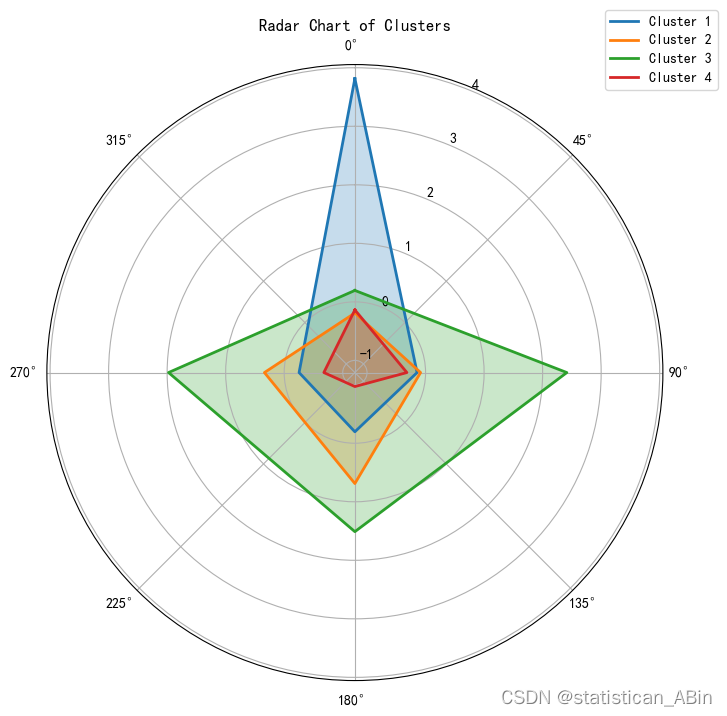
接下来可视化主成分
# 可视化主成分 1 的载荷
plt.figure(figsize=(8, 4))
colors = ['red', 'green', 'blue', 'yellow', 'purple', 'orange', 'pink', 'brown', 'gray', 'cyan']
plt.bar(pca_loadings_df.columns, pca_loadings_df.loc['PC1'], color=colors)
plt.xlabel('Features')
plt.ylabel('Loadings for PC1')
plt.title('PCA Loadings for Principal Component 1')
plt.show()
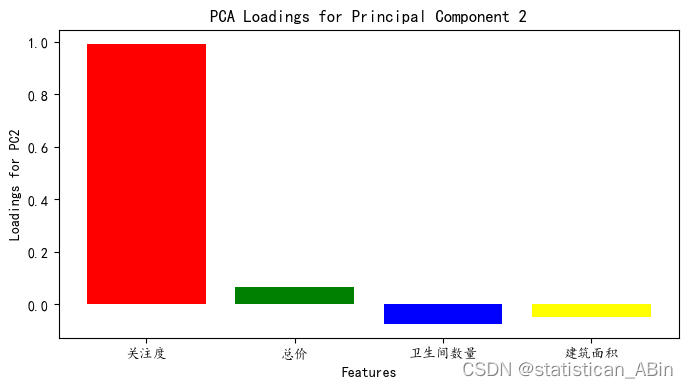
# 可视化主成分 2 的载荷
plt.figure(figsize=(8, 4))
plt.bar(pca_loadings_df.columns, pca_loadings_df.loc['PC2'], color=colors)
plt.xlabel('Features')
plt.ylabel('Loadings for PC2')
plt.title('PCA Loadings for Principal Component 2')
plt.show() 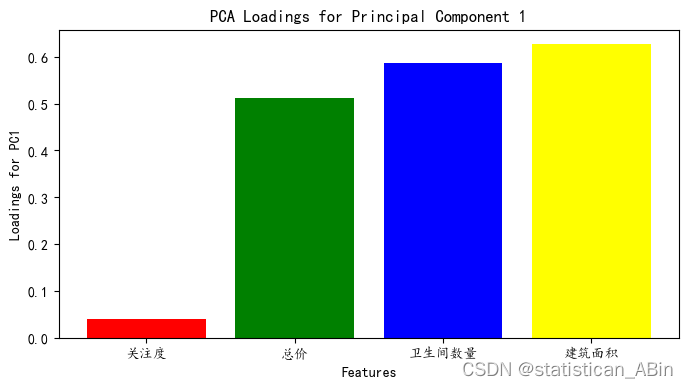
 三、小结
三、小结
本研究通过对房价数据的聚类分析,将房价数据分为了不同的类别,发现了房价的分布特征和规律。通过特征选择和标准化处理,提高了聚类分析的准确性和可靠性。使用手肘方法和轮廓系数确定了最佳的 K 值,为聚类分析提供了科学依据。通过 PCA 进行降维,可视化了主成分,进一步深入了解了房价数据的内在结构。本研究的结果对于购房者、房地产开发商、政府部门等都具有重要的参考价值,可以为相关决策提供科学依据。
创作不易,希望大家多点赞关注评论!!!(类似代码或报告定制可以私信)