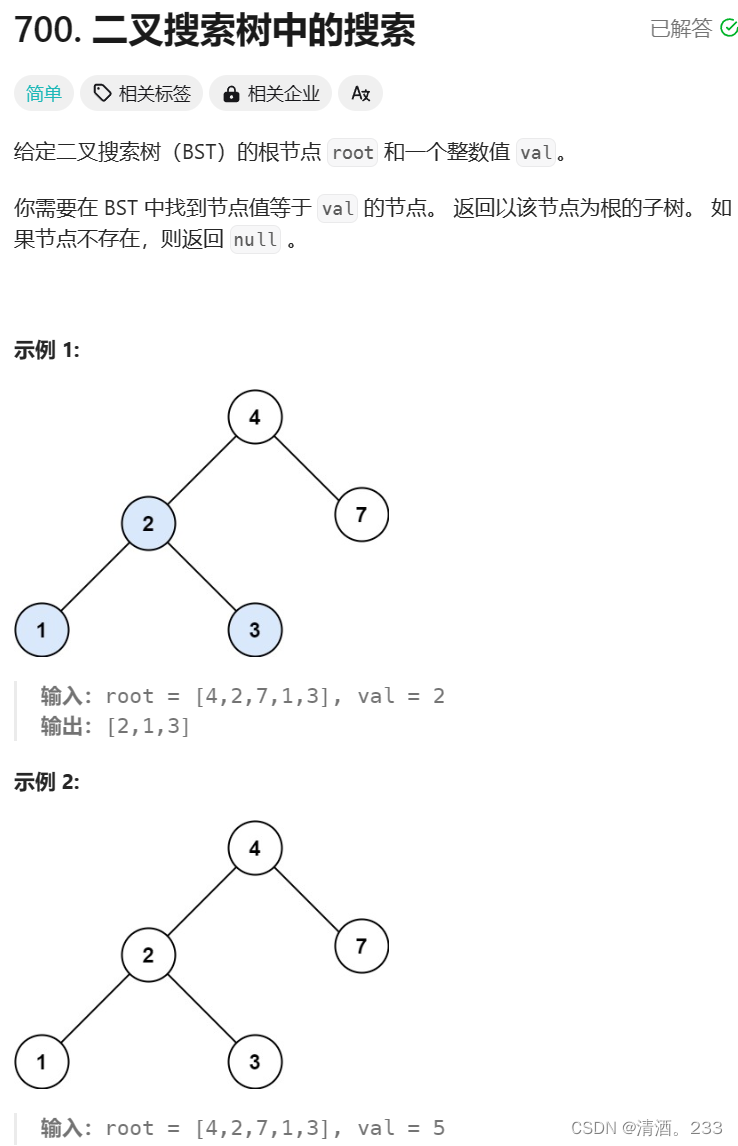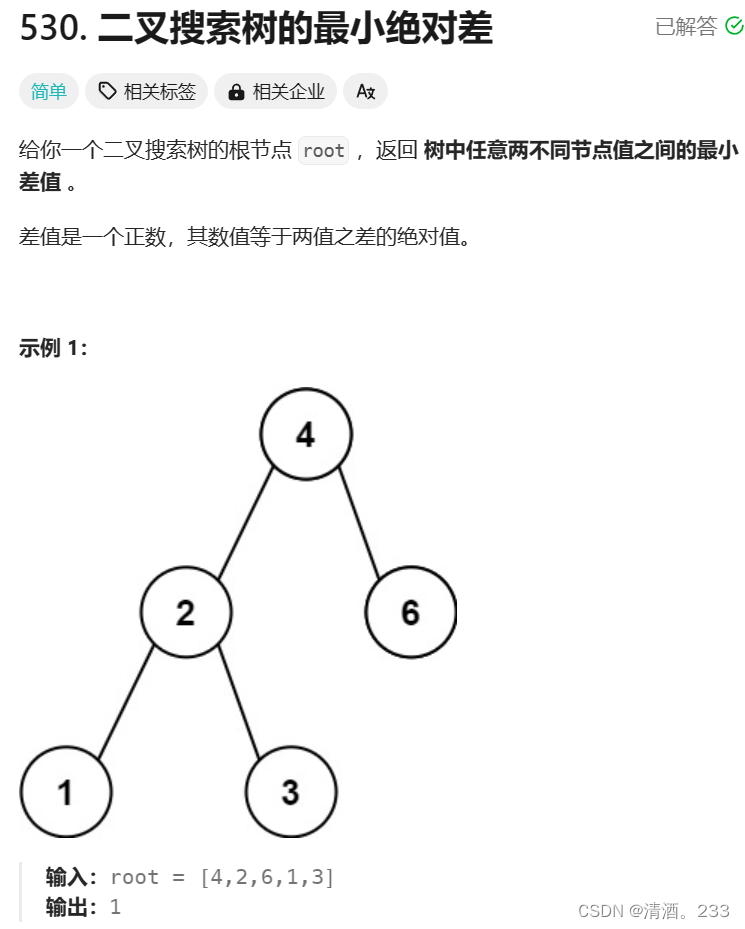
代码解决

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 初始化最小差值为INT_MAX
    int result = INT_MAX;
    // 用于记录前一个节点的指针
    TreeNode* pre = nullptr;
    
    // 中序遍历函数
    void traversal(TreeNode* node)
    {
        // 如果节点为空，则返回
        if(node == nullptr) return;
        
        // 递归遍历左子树
        traversal(node->left);
        
        // 处理当前节点
        if(pre != nullptr)
        {
            // 更新最小差值
            result = min(result, node->val - pre->val);
        }
        // 更新前一个节点指针
        pre = node;
        
        // 递归遍历右子树
        traversal(node->right);
    }
    
    // 获取二叉搜索树中任意两节点值之间的最小差值
    int getMinimumDifference(TreeNode* root) 
    {
        // 开始中序遍历
        traversal(root);
        // 返回计算出的最小差值
        return result;
    }
};

1. 定义一个全局变量 result 用于记录最小差值，初始化为 INT_MAX。
2. 定义一个全局变量 pre 用于记录中序遍历过程中的前一个节点。
3. 定义一个辅助函数 traversal，它接受当前节点作为参数。
4. 如果当前节点为空，则返回。
5. 递归地遍历左子树。
6. 处理当前节点：
   • 如果 pre 不为空，更新最小差值 result 为当前节点值与 pre 节点值之差的最小值。
   • 更新 pre 为当前节点。
7. 递归地遍历右子树。
8. 在 getMinimumDifference 函数中，开始中序遍历，并返回计算出的最小差值 result。

这个算法的时间复杂度是 O(n)，因为每个节点都会被访问一次，其中 n 是树中节点的数量。空间复杂度也是 O(n)，因为需要存储递归调用的栈。