AI变声和音乐创作的基础
声音本质上是人类可察觉范围内的气压周期性波动, 即声波
声波是一种连续信号,在任意时间内的声音信号有无数个取值。对于只能读取有限长数组计算机来说,我们需要将连续的声音信号转换为一个离散的序列,即数字化表示。
1.音频采样 (sampling)
采样是在固定时间间隔上测量连续信号,并将这些间隔信号转换为离散数值的过程。
采样率(sampling rate,也叫采样频率,sampling frequency)指的是每秒测量信号数值的次数,其单位为赫兹(Hz)。
-
CD音质的音频一般采用44100Hz的采样率,即每秒钟测量了44100次信号的数值。
-
高清(High-resolution)音频的采样率一般为192000赫兹,即192千赫兹。
-
语音模型常用的采样率为16,000赫兹,即16千赫兹。
1.1 采样幅值
幅值是描述声音在任意瞬间的气压大小,使用分贝(dB)作为单位
人类感知到的幅值强度称为响度
正常的说话声音响度在60分贝以下;一场摇滚演出的响度大概在125分贝,几乎是人耳的极限。
- 在数字音频中,每个采样点记录某个时间点上的声波幅值
1.2 位深度
-
采样点的位深度决定了采样点的数值可以有多少种变化,即采样的精度
-
位深度越大,数字化表示就可以越准确地记录下原始的连续声波
在这一量化过程中,原始的连续幅值被约减到最近的离散值上,因此量化过程会引入噪声。位深度越大,量化噪声则越小。
最常见的音频位深度为16比特或24比特。比特是一个二进制单位,
表示了声波的连续幅值被数字化后可以取值的范围:16比特有65,536种可能的取值,而24比特有16,777,216种可能的取值。
在实际应用中,16比特音频的量化噪声已达到了几乎不可辨别的程度。
1.3 重采样
改变音频采样频率,频率变高(大)为上采样,频率变低(小)为下采样
信号的原始采样率为8千赫兹时,即信号每秒钟会包含8000个采样点,根据奈奎斯特采样定理,我们知道该信号不会包含高于4千赫兹的频率成分。
假设两个采样点中间的原始连续信号呈一条平滑的曲线:
-
上采样是对曲线的估计计算得到两个采样点中间的额外数值。
-
下采样首先要通过低通滤波器过滤高于 奈奎斯特极限频率 的成分,之后重新按低频率采样。
能通过简单的每隔一个采样点丢弃一个采样点来进行2倍的下采样, 会造成信号的失真,即混叠失真。
2.音频的时域-频域
音频信号的频域(谱)和其时域(波形)所包含的信息完全相同,他们只是相同数据的不同视角。
-
时域波形表示的是幅值随时间的变化
-
频谱表示的是各个频率成分在该时间段内的强度
2.1 音频的时域
采样点随着时间变化的数值被标记在直角坐标系中
这种可视化表示方法可以很好地帮助我们辨别声音信号中的某些特征,
用librosa来绘制音频信号的波形图:
import librosa
import librosa.display
import matplotlib.pyplot as plt
array, sampling_rate = librosa.load(librosa.ex("trumpet"))
plt.figure().set_figwidth(12)
librosa.display.waveshow(array, sr=sampling_rate)
# y轴表示的是信号的幅值,x轴则表示时间
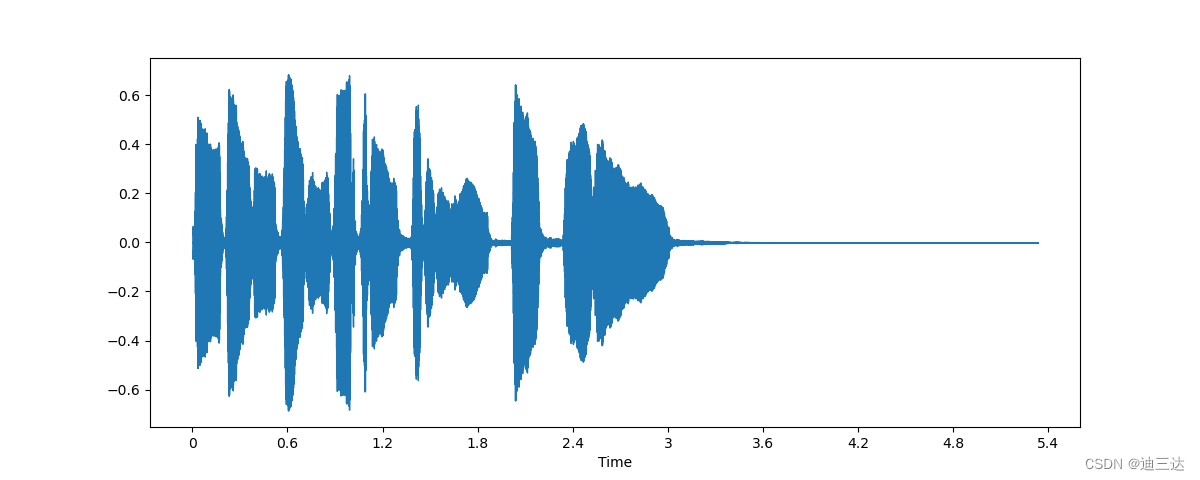
2.2 音频的频域
即音频的 频谱(spectrum) or 频域(frequency domain)
频谱通过离散傅里叶变换(Discrete Fourier Transform, DFT)求得,描述音频信号中每个频率成分的强度
使用numpy的rfft()函数来绘制小号声音的频谱图,使用整段音频的前4096个采样点计算DFT,这差不多是第一个音符的长度:
import numpy as np
dft_input = array[:4096]
# 计算 DFT
window = np.hanning(len(dft_input))
windowed_input = dft_input * window
dft = np.fft.rfft(windowed_input)
# 计算频谱的幅值,转换为分贝标度
amplitude = np.abs(dft)
amplitude_db = librosa.amplitude_to_db(amplitude, ref=np.max)
# 计算每个DFT分量对应的频率值
frequency = librosa.fft_frequencies(sr=sampling_rate, n_fft=len(dft_input))
plt.figure().set_figwidth(12)
plt.plot(frequency, amplitude_db)
plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude (dB)")
plt.xscale("log")
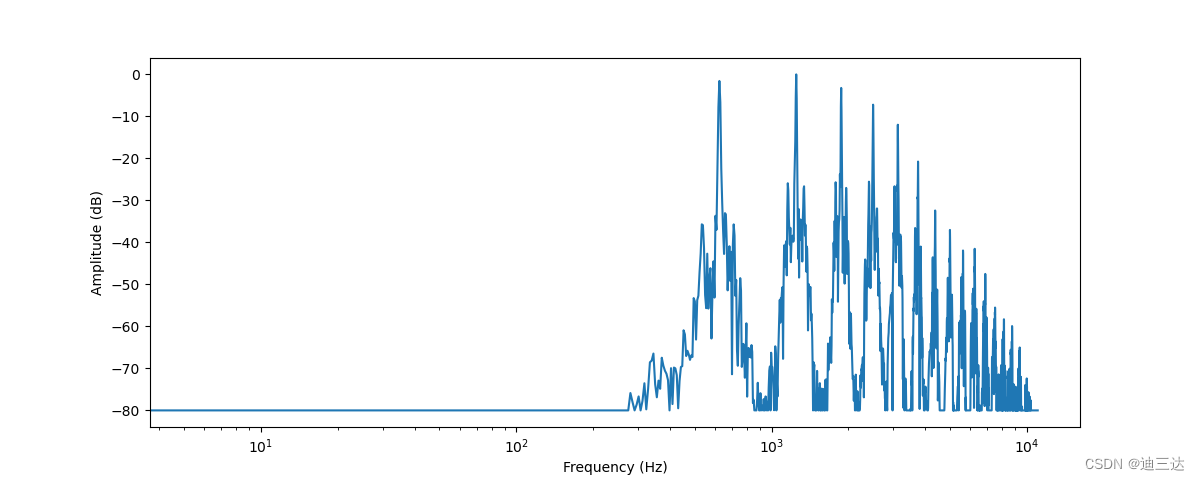
这张图向我们展示了截取的音频片段中各个频率成分的强度。图中的x轴是频率的值,一般采用对数表示;y轴则对于频率的幅值。
可以看到这张频谱图中有几个峰值。这些峰值对应着当前音符的泛音频率,且更高的泛音声音更小。可以看到首个峰对应的频率在620赫兹左右,这说明当前演奏的音符的音高是E♭。
计算DFT所得到的频谱是由复数组成的序列,每个复数都包含了实部和虚部。我们可以使用np.abs(dft)来计算频谱的绝对值(又称模、幅值)。实部和虚部的夹角组成的序列也成为相位谱,但在机器学习应用中我们通常不关注这一部分。
我们使用了librosa.amplitude_to_db()函数将幅值转换为了分贝标度,方便我们观察频谱的细节。有时人们也使用测量能量而非幅值的能量谱(power spectrogram),其值为幅值的平方。
2.3 时频谱
描绘频率成分随着时间的变化
在一段乐器演奏中,演奏者实际上吹奏了几个不同频率的音符。 频谱只能表示一个短暂时间段内各个频率成分的总体幅值
时频谱表示了音频信号中各个频率成分随时间变化的过程。它可以在一张图中看到时间、频率和幅值的所有信息。
时频谱是信息量最大的音频工具之一:
-
在分析音乐文件时,时频谱可以清晰地展示各个乐器和人声在音乐整体中所占的部分
-
在语音文件中,可以在时频谱里看到每个元音音节以及它们频率成分的差异。
这里的解决方法是我们可以进行多次的DFT,每次DFT都覆盖一小段不同的时间段,然后再把所有的频谱堆叠起来,这样就构成了时频谱(spectrogram)
import numpy as np
D = librosa.stft(array) # Short Time Fourier Transform, STFT
S_db = librosa.amplitude_to_db(np.abs(D), ref=np.max)
plt.figure().set_figwidth(12)
librosa.display.specshow(S_db, x_axis="time", y_axis="hz")
plt.colorbar()
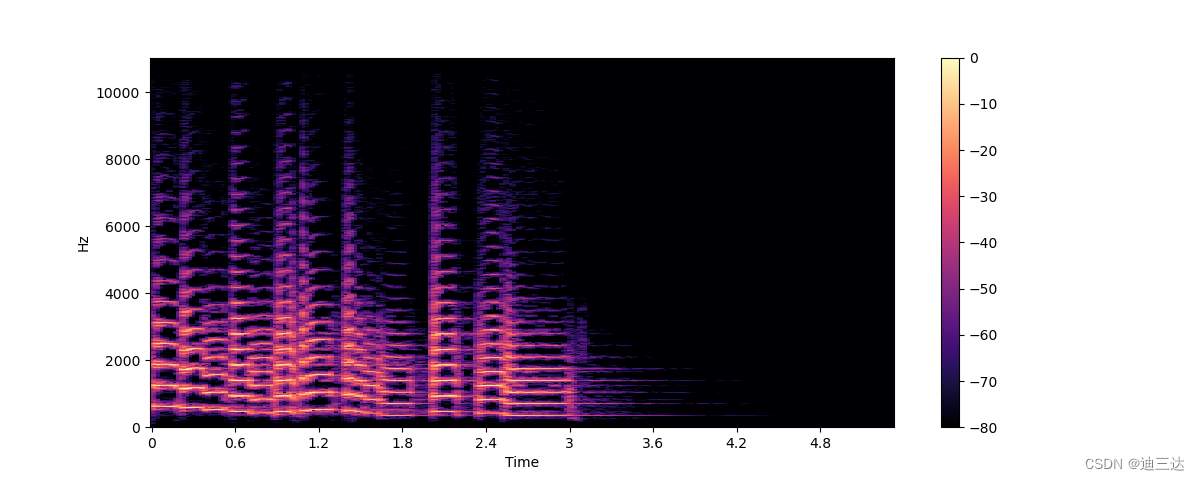
图解:
- x轴表示的是和波形图中相同的时间
- y轴现在表示着不同的频率,以赫兹(Hz)为单位
- 颜色的强度表示着当前时间点和频率的幅值强度,使用分贝(dB)标度
时频谱计算步骤:
1. 首先截取很短的音频片段(通常只有几毫秒),然后对每个片段计算其离散傅里叶变换(DFT);
2. 获得所有片段的频谱之后,我们再将频谱延时间轴堆叠起来,这样就得到了我们的时频谱
时频谱图像的每个垂直切片都是一个单独的频谱图
3.梅尔时频谱
一种时频谱变体,与标准时频谱相比,梅尔谱可以捕捉更多人类可感知的音频特征,在语音识别、、音乐等任务中更常用。
标准时频谱的频率(y轴)是赫兹的线性变化。 由于人类听觉系统对于低频率声音的变化更敏感,对于高频率声音的变化则较不敏感。这一敏感度的变化是随频率的上升呈对数关系下降的。
S = librosa.feature.melspectrogram(y=array, sr=sampling_rate, n_mels=128, fmax=8000)
S_dB = librosa.power_to_db(S, ref=np.max)
plt.figure().set_figwidth(12)
librosa.display.specshow(S_dB, x_axis="time", y_axis="mel", sr=sampling_rate, fmax=8000)
plt.colorbar()
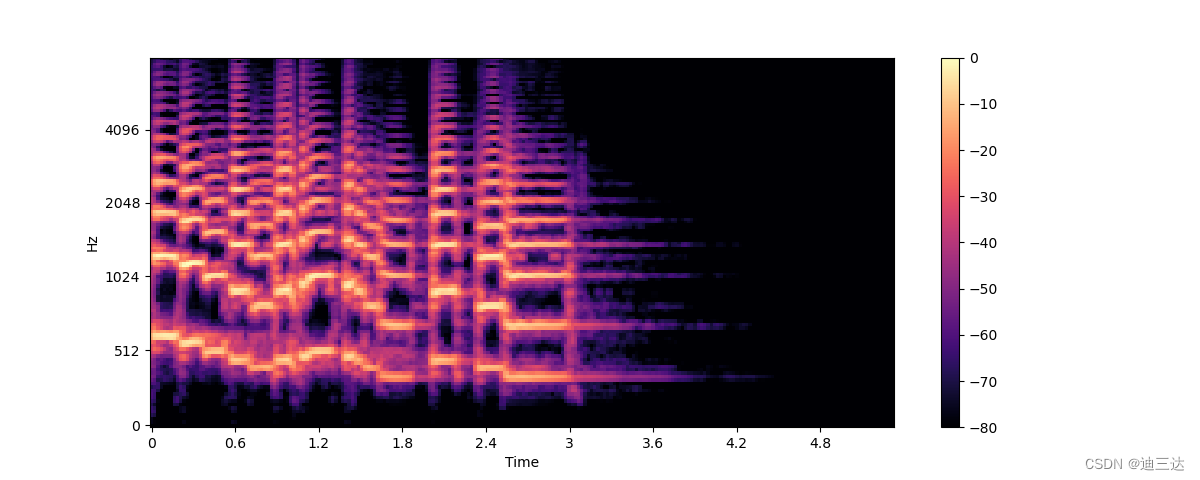
- 梅尔滤波器组:
梅尔标度作为一种感知标度,通过梅尔滤波器组,模拟人耳对于频率的非线性感知。
n_mels代表梅尔滤波器组中的滤波器个数
梅尔滤波器组会计算一组频率范围,这些频率范围会将整个频谱分割成许多部分
每个频率范围都对应滤波器组中的一个滤波器
滤波器的形状和间隔是模拟人耳对不同频率的感知差异而计算得出
常用的n_mels取值为40或80
fmax则代表我们想选取的最大频率(以赫兹为单位)
- 梅尔谱的计算过程中需要对信号进行滤波,因此梅尔谱的特征有损过程。
将梅尔谱转化回波形比标准时频谱更加困难,我们需要估计在滤波过程中丢失的频率成分。
- HiFiGAN声码器可以将梅尔谱转化回波形。
4.其他
-
反向短时傅里叶变换(inverse STFT)可将时频谱转换回原始的波形 这需要时频谱的强度谱之外,也需要时频谱的相位谱,目前的机器学习模型大多只能生成强度谱
-
相位重建(phase reconstruction)方法,包括传统的Griffin-Lim算法,或者使用一种被称为声码器(vocoder)的神经网络来从时频谱还原其波形
-
时频谱的作用不仅在于音频的可视化,许多机器学习模型也会使用时频谱作为模型的输入和输出而不直接使用音频的波形
Reference
- 本文内容借鉴: https://huggingface.co/learn/audio-course/zh-CN/chapter1/introduction