视频资源B站：动手学习深度学习——李沐

目标

• 介绍深度学习景点和最新模型
  • LeNet AlexNet VGG ResNet LSTM BERT…
• 机器学习基础
  • 损失函数，目标函数，过拟合，优化
• 实践
  • 使用pytorch实现介绍的知识点
  • 在真实数据上体验算法效果

内容

• 深度学习基础——线性神经网络，多层感知机
• 卷积神经网络——LeNet，AlexNet，VGG，Inception，ResNet
• 循环神经网络——RNN，GRU，LSTM，seq2seq
• 注意力机制——Attention，Transformer
• 优化算法——SGD，Momentum，Adam
• 高性能计算——并行，多GPU，分布式
• 计算机视觉——目标检测，语义分割
• 自然语言处理——词嵌入，BERT

将学到什么

• What
  • 深度学习里有那些技术
• How
  • 如何实现和调参
• Why
  • 背后的原因（直觉，数学）

1.N维数组样例

N维数组是机器学习和神经网络的主要数据结构

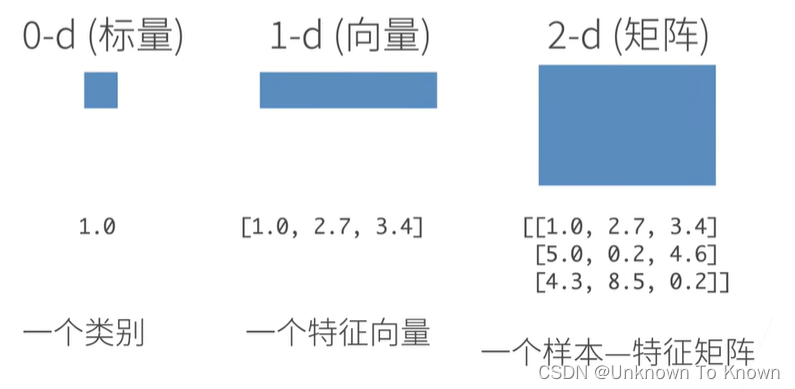
2.访问2维数组元素

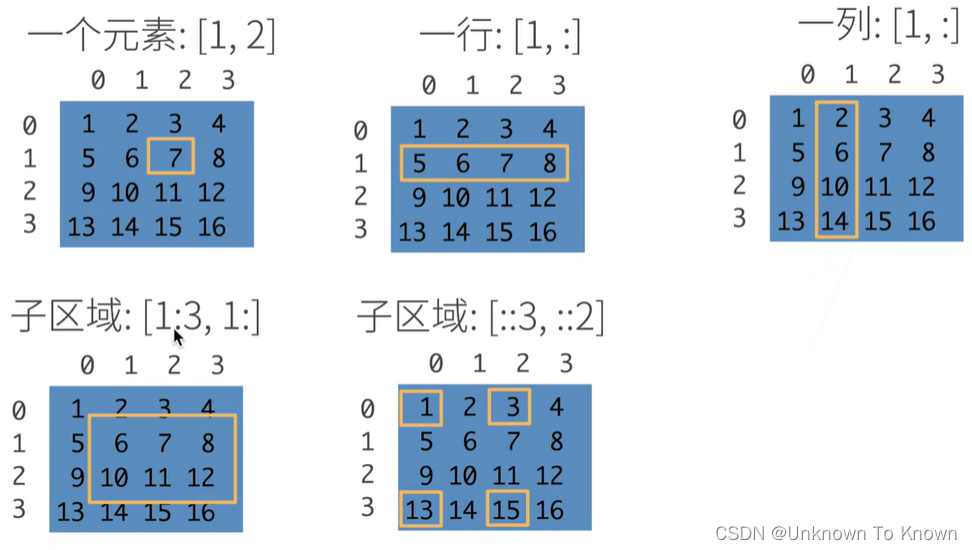
3.数据操作

​ 首先，我们导入torch，注意，虽然它被称为pytorch，但我们应该导入torch而不是pytorch

import torch
#张量表示一个数值组成的数组，这个数组可能有多个纬度
x = torch.arange(12)#输出：1 2 3 ...12

x.shape#输出：torch.Size([12])
x.numel#输出：12

#要改变一个张量的形状而不改变元素数量和元素值，我们可以调用reshape函数
x = x.reshape(3,4)
#输出：
。。。。。。不再过多的描述

4.线性代数

矩阵相当于一个扭曲空间，把下图中的蓝线和绿线，扭曲到不同方向和长度

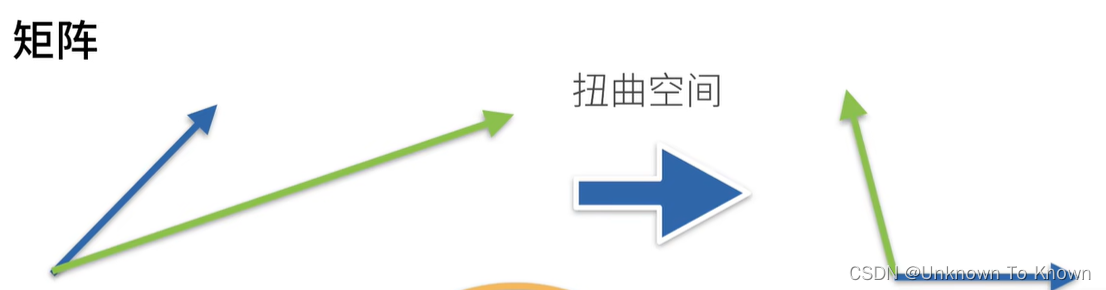
5.矩阵计算

6.自动求导

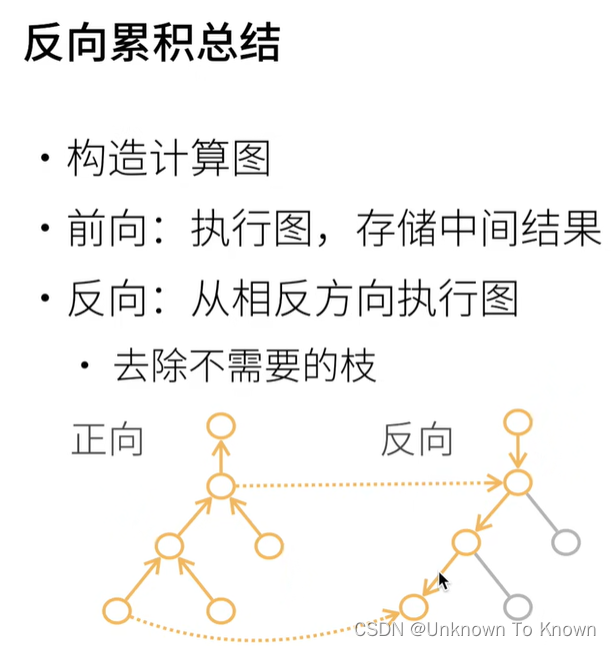
复杂度：

• 计算复杂度：O(n)，n为操作字个数
  • 通常正向和反向的代价类似
• 内存复杂度：O(n)，因为需要存储正向的所有中间结果
• 跟正向累积对比
  • O(n)计算复杂度用来计算一个变量的梯度
  • O(1)内存复杂度