神经元
生物神经元:
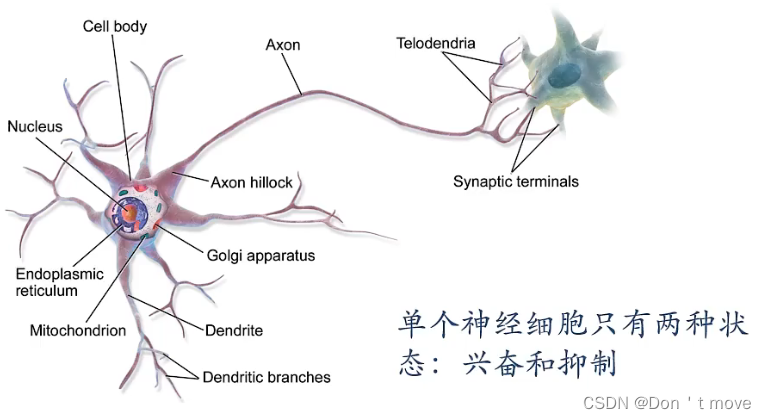
平时处于抑制状态,当接受信息量达到一定程度后进入兴奋状态。
人工神经元:
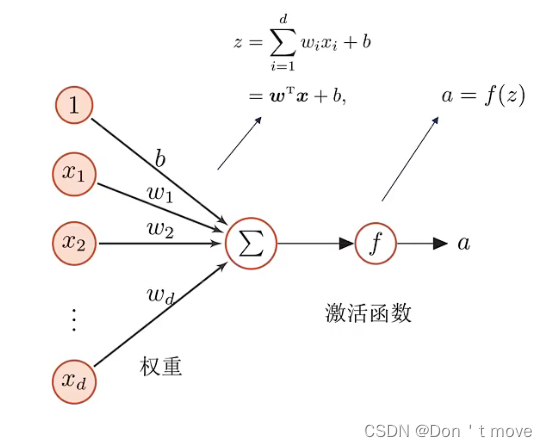
一个人工神经元大致有两个步骤:
一是收集信息,如上图中
x
1
,
⋯
,
x
d
x_1,\cdots,x_d
x1,⋯,xd表示神经元可以接受的外界信号,对这些信号进行加权汇总(不同外界信号对神经元作用的权重不同,即
w
1
,
⋯
,
w
d
w_1,\cdots,w_d
w1,⋯,wd),最后加上用来调节阈值的偏置
b
b
b,得到上图中的汇总信息
z
z
z。
二是将加权汇总的信息
z
z
z经过一个激活函数最后得到神经元的活性值
a
a
a。
实质上人工神经元就是一个简单的线性模型。
激活函数
对不同类型的人工神经元,其一般只在激活函数的设计上有所不同,但是要将汇总信息映射到对应的区间内,必须要求激活函数具有以下性质:
- 激活函数必须是连续可导(允许少数点上不可导)的非线性函数:可导的激活函数可以直接利用数值优化的方法(例如梯度下降)来学习网络参数。
- 激活函数及其导函数要尽可能的简单:这样有利于提高网络计算效率。
- 激活函数导数的值域要在一个合适的区间内:值域区间不能太大也不能太小,否则会影响训练的效率和稳定性。
- 激活函数应该能够反应汇总信息的大小:也就是说如果z越小,激活函数应该尽可能更加地反映出z小所对应的状态。
- 大多数的激活函数都是单调递增的。
常用的激活函数有以下三类:
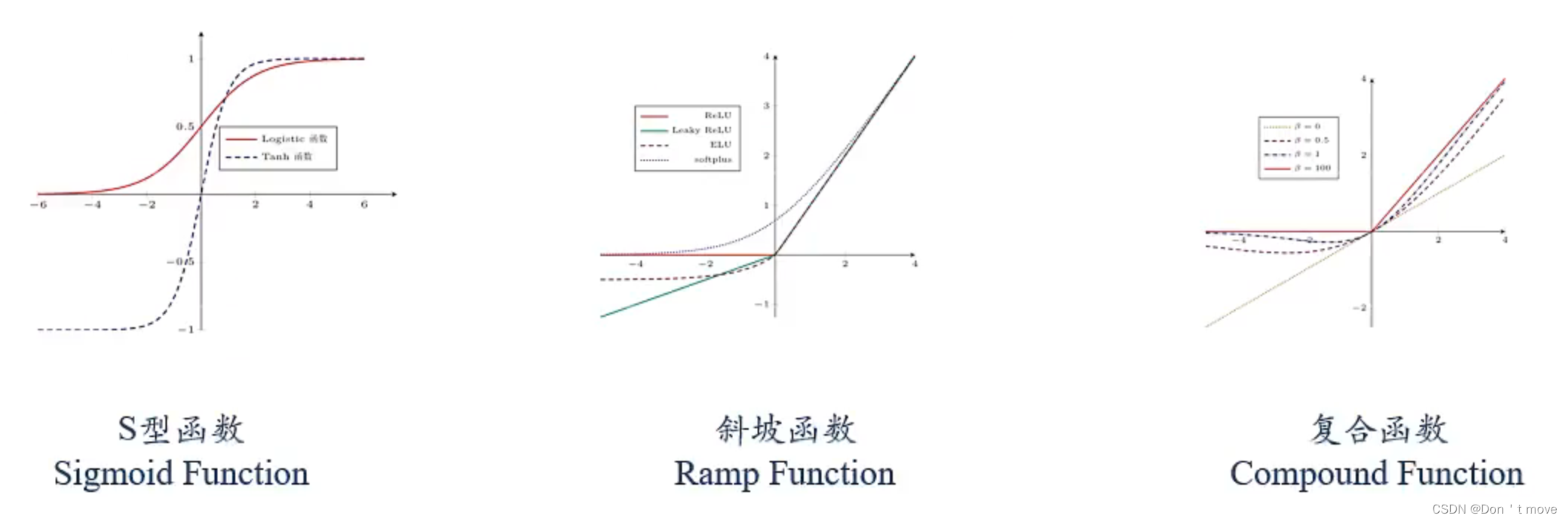
S型函数
较为典型的就是之前说过的Logistic函数
σ
(
x
)
=
1
1
+
exp
(
−
x
)
\sigma(x)=\frac{1}{1+\exp(-x)}
σ(x)=1+exp(−x)1
此外还有tanh函数,他的值域在
(
−
1
,
1
)
(-1,1)
(−1,1)之间
tanh
(
x
)
=
exp
(
x
)
−
exp
(
−
x
)
exp
(
x
)
+
exp
(
−
x
)
\tanh(x)=\frac{\exp(x)-\exp(-x)}{\exp(x)+\exp(-x)}
tanh(x)=exp(x)+exp(−x)exp(x)−exp(−x)
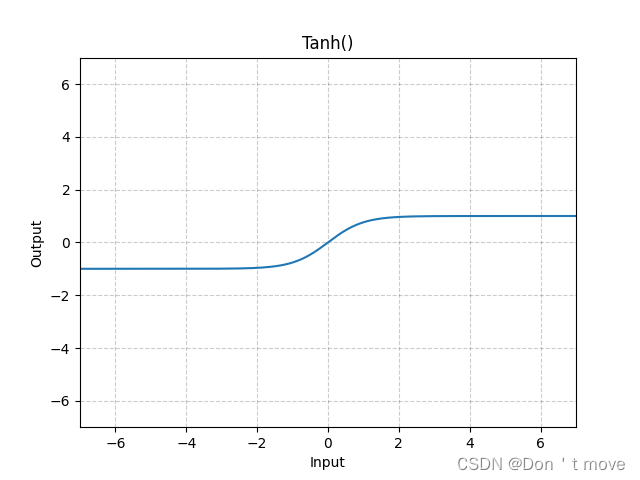
上述两个激活函数存在以下关系:
tanh
(
x
)
=
2
σ
(
2
x
)
−
1
\tanh(x)=2\sigma(2x)-1
tanh(x)=2σ(2x)−1
通常情况下,只要不是要求神经元输出结果一定要是正的,最好选择tanh函数来代替Logistic函数,因为tanh函数在优化上更好。
S型函数的性质:
- 是饱和函数:意思是说S型函数两端(横坐标趋向于正无穷和负无穷的两端)的梯度都是接近于0的
- tanh函数是零中心化的,而logistic函数输出恒大于0 :非零中心化的输出会使得其后一层的神经元输入发生偏置偏移(bias shift),并进一步使得梯度下降收敛速度变慢(没搞明白)
斜坡函数
典型的斜坡函数是ReLU函数(修正的线性单元)
R
e
L
U
(
x
)
=
max
(
0
,
x
)
\mathrm{ReLU}(x)=\max(0,x)
ReLU(x)=max(0,x)

ReLU函数是一般神经网络的首选函数
ReLU函数的性质:
- 计算上更加高效
- 生物学合理性:单侧抑制(当神经元处于抑制状态时不区分抑制程度)、款兴奋边界(当神经元处于兴奋状态时区分兴奋的程度,即有多兴奋)
- 在一定程度上缓解梯度消失问题
由于ReLU函数单侧抑制的性质,假如输入数据信息全部处于小于0一侧,那么ReLU函数的输出将变成0,对应的导数(梯度)也是0,从而无法更新参数,导致该神经元一直处于非激活状态,一直输出0,这就是所谓的死亡ReLU问题(Dying ReLU Problem)。
为了解决这个问题,提出了Leaky ReLU函数:
L
e
a
k
y
R
e
L
U
(
x
)
=
{
x
i
f
x
>
0
γ
x
i
f
x
≤
0
=
max
(
0
,
x
)
+
γ
min
(
0
,
x
)
\mathrm{LeakyReLU}(x)=\left\{\begin{aligned} &x &if\ \ x>0\\ &\gamma x &if\ \ x\leq0 \end{aligned}\right.=\max(0,x)+\gamma\min(0,x)
LeakyReLU(x)={xγxif x>0if x≤0=max(0,x)+γmin(0,x)
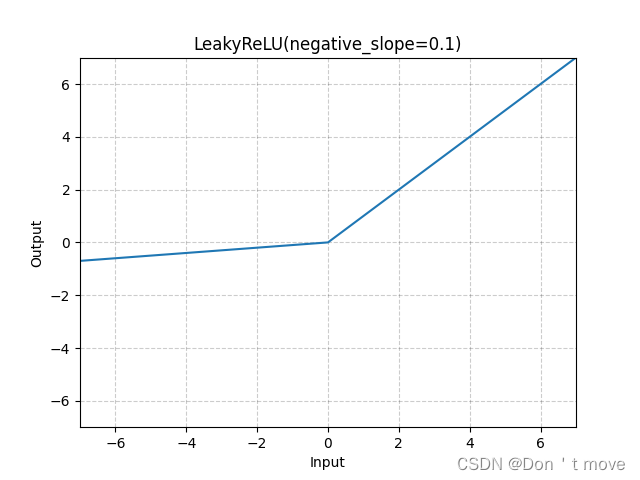
同样ReLU函数也是非零中心化的函数,基于此又提出了近似的零中心化的非线性函数
E
L
U
(
x
)
=
{
x
i
f
x
>
0
γ
(
exp
(
x
)
−
1
)
i
f
x
≤
0
=
max
(
0
,
x
)
+
min
(
0
,
γ
(
exp
(
x
)
−
1
)
)
\mathrm{ELU}(x)=\left\{\begin{aligned} &x&if\ \ x>0\\ &\gamma(\exp(x)-1)&if\ \ x\leq0 \end{aligned}\right.=\max(0,x)+\min(0,\gamma(\exp(x)-1))
ELU(x)={xγ(exp(x)−1)if x>0if x≤0=max(0,x)+min(0,γ(exp(x)−1))

除了这些之外,还有一个对ELU函数进行处理,使其尽可能接近ReLU函数的版本,也可以说是ReLU函数的平滑版本,叫做Softplus函数
S
o
f
t
p
l
u
s
(
x
)
=
log
(
1
+
exp
(
x
)
)
\mathrm{Softplus}(x)=\log(1+\exp(x))
Softplus(x)=log(1+exp(x))

复合函数
复合激活函数都比较复杂,下面介绍几种
Swish函数
一种自门控(Self-Gated) 激活函数
s
w
i
s
h
(
x
)
=
x
σ
(
β
x
)
\mathrm{swish}(x)=x\sigma(\beta x)
swish(x)=xσ(βx)
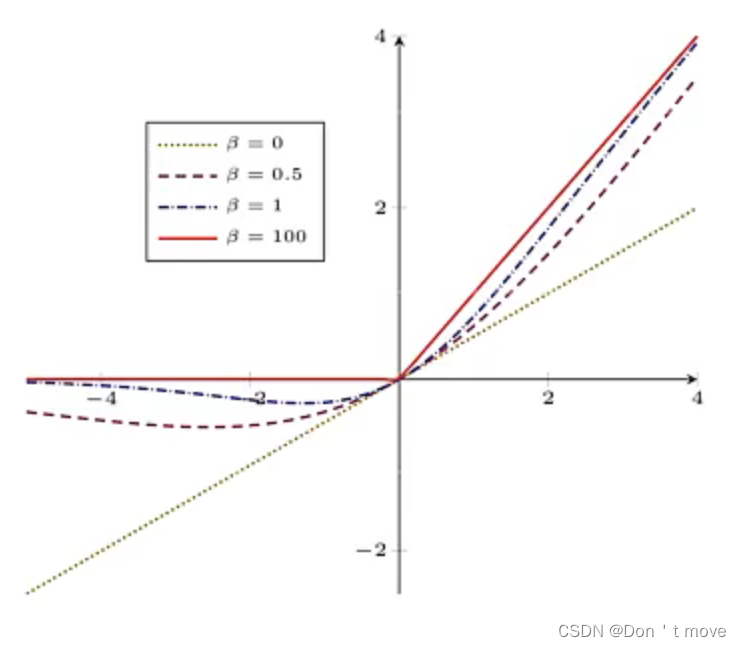
其中
σ
\sigma
σ函数就是上面提到的Logistic函数,由于
σ
\sigma
σ函数取值在
(
0
,
1
)
(0,1)
(0,1)之间,近似门控(gate,有0或1两种状态),而
σ
\sigma
σ函数的取值不只有这两种状态,而是在区间中取值,假如说对于式子
x
σ
(
x
)
,
σ
(
x
)
=
0.5
x\sigma(x),\sigma(x)=0.5
xσ(x),σ(x)=0.5,代表的意思就是只允许一半的信息通过,这种就是所谓的软门控(soft-gate),而所谓自门控(self-gate),只是为了强调信息是由传入的信息
x
x
x本身来控制的。
对于上式中的
β
\beta
β用来控制门控允许通过信息的多少,可以参照上图进行理解,在
β
\beta
β的不同取值下,图像在上图红色实线(
β
=
100
\beta=100
β=100)到黄绿色点线(
β
=
0
\beta=0
β=0)之间变换。
高斯误差线性单元(Gaussian Error Linear Unit,GELU)
G
E
L
U
(
x
)
=
x
P
(
X
≤
x
)
\mathrm{GELU}(x)=xP(X\leq x)
GELU(x)=xP(X≤x)
其中
P
(
X
≤
x
)
P(X\leq x)
P(X≤x)是高斯分布
N
(
μ
,
σ
2
)
N(\mu,\sigma^2)
N(μ,σ2)的累积分布函数,也是一个S型函数。
μ
,
σ
\mu,\sigma
μ,σ为超参数,一般令
μ
=
0
,
σ
=
1
\mu=0,\sigma=1
μ=0,σ=1
由于高斯分布的累积分布函数为S型函数,因此GELU可以通过下面的公式用Tanh函数或者Logistic函数来近似替代:
G
E
L
U
(
x
)
≈
0.5
x
(
1
+
t
a
n
h
(
2
N
(
x
+
0.044715
x
3
)
)
)
G
E
L
U
(
x
)
≈
x
σ
(
1.702
x
)
\begin{aligned} &\mathrm{GELU}(x)\approx0.5x(1+\mathrm{tanh}(\sqrt{\frac{2}{N}}(x+0.044715x^3)))\\ &\mathrm{GELU}(x)\approx x\sigma(1.702x) \end{aligned}
GELU(x)≈0.5x(1+tanh(N2(x+0.044715x3)))GELU(x)≈xσ(1.702x)
人工神经网络
人工神经网络由大量神经元和人工神经网络以及它们之间的有向连接构成。构建人工神经网络需要考虑三个方面:
- 神经元的激活规则:神经元输入到输出间的映射关系,一般为非线性函数(激活函数)
- 网络的拓扑结构:不同神经元直接的连接关系
- 学习算法:通过训练数据来学习网络的参数。这里特别注意,不是所有神经网络都是通过梯度下降方法来学习的。
网络拓扑结构主要有三种:
- 前馈网络:下图a,信息由前向后单向传递
- 记忆网络:下图b,内部存在循环边,需要记录神经元在某个时刻的状态(记忆)
- 图网络:下图c,把神经元分为多个组,每组神经元之间的连接关系是由图定义的。

通常情况下大多数神经网络都是三种结构的复合体。