---

前言

860.柠檬水找零

思路

很简单，贪心只有一个，如果20优先用10+5找零，因为5更加万能一些

方法一

class Solution(object):
    def lemonadeChange(self, bills):
        """
        :type bills: List[int]
        :rtype: bool
        """
        fives, tens = 0,0
        if fives:
            print("fives")
        for i in range(len(bills)):
            print(fives,tens)
            if bills[i] == 5:
                fives += 1
            elif bills[i] == 10:
                tens += 1
                if fives: fives -= 1
                else: return False
            elif bills[i] == 20:
                if fives and tens:
                    fives -= 1
                    tens -= 1
                elif fives >= 3:
                    fives -= 3
                else: return False
            else: 
                return False
        return True

406.根据身高重建队列

思路

注意思想：不能两者一起考虑，只能一个一个来
根据身高从大到小排序之后再去考虑数目的问题；【先k后h】

• 本题的突破口在于，排序好之后只需要按照k来插入 因为每个人前面一定比他高，所以可以放心地根据k值来进行插入
• 

方法一

注意点今天心态有点崩溃，太晚了就没有写了

1. 需要重新定义一个que而不是直接在people里面插入，因为people会因为插入长度改变的，后面的索引会出错
2. python中list插入有insert，插入位置 que.insert(p[1], p)

class Solution:
    def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
    	# 先按照h维度的身高顺序从高到低排序。确定第一个维度
        # lambda返回的是一个元组：当-x[0](维度h）相同时，再根据x[1]（维度k）从小到大排序
        people.sort(key=lambda x: (-x[0], x[1]))
        que = []
	
	# 根据每个元素的第二个维度k，贪心算法，进行插入
        # people已经排序过了：同一高度时k值小的排前面。
        for p in people:
            que.insert(p[1], p)
        return que

452. 用最少数量的箭引爆气球

边界重合也是算可以一个箭射中两个

思路

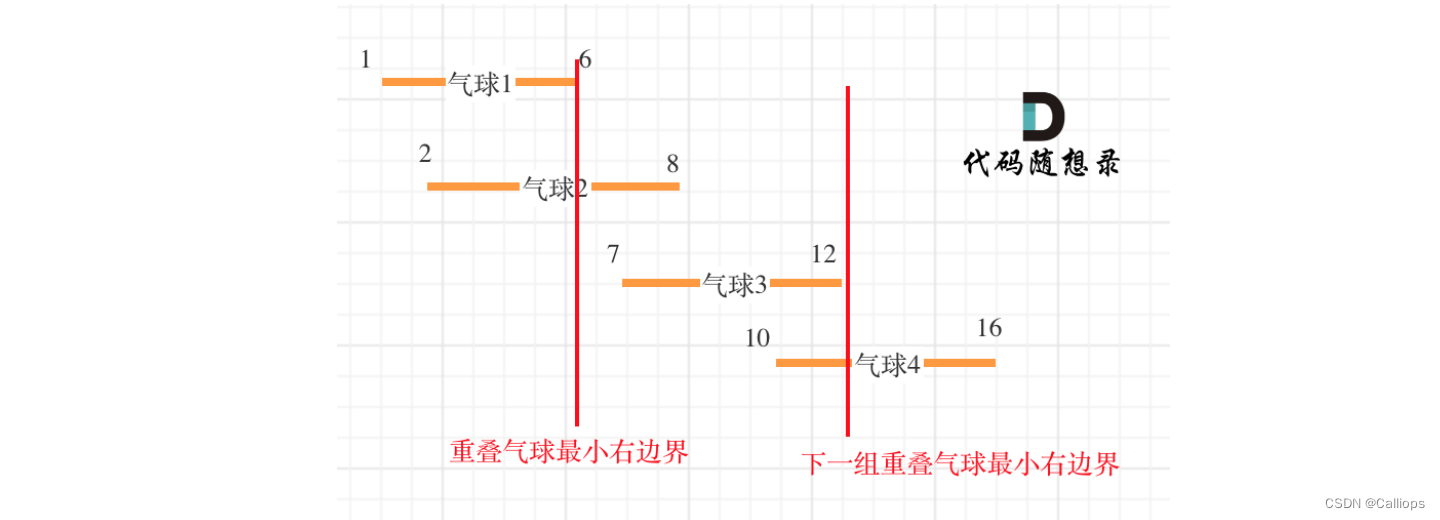
首先需要能画出下面的图；依据左边界进行排序
两种情况讨论

1. 如果i的左边界大于i-1的右边界，那么就不重叠，肯定需要result++；
2. 如果i的左边界小于等于i-1的右边界，那就不需要加一，同时右边界换成min i和i-1 的小的值，这样下一个跟新的右边界比较
   

方法一

自己写的注意点

1. range从1开始，因为是和i-1比较，并且result默认初始值为1。这也好理解，如果两个气球没有交集，需要多射一次；
2. 第二种我也给出了不改变原数组的写法；
3. 排序还可以用这个写法 points.sort(key=lambda x: x[0])

class Solution(object):
    def findMinArrowShots(self, points):
        """
        :type points: List[List[int]]
        :rtype: int
        """
        result = 1
        points = sorted(points, key=lambda x: x[0], reverse=False)
        for i in range(1, len(points)):
            if points[i][0] > points[i-1][1]: result += 1
            else:
                points[i][1] = min(points[i][1],points[i-1][1])

        return result

class Solution: # 不改变原数组
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        points.sort(key = lambda x: x[0])
        sl,sr = points[0][0],points[0][1]
        count = 1
        for i in points:
            if i[0]>sr:
                count+=1
                sl,sr = i[0],i[1]
            else:
                sl = max(sl,i[0])
                sr = min(sr,i[1])
        return count

---

总结