宝贝们,好久不见,甚是想念🤗小吉断更了差多有10多天,在断更的日子里,小吉也有在好好学习数据结构与算法,但是学的并不多而且学的并不是很认真。主要是中途笔记本屏出现问题了(这件事有点让小吉我没法好好沉下心来学习,而且不用电脑学起来有点费劲,不能边学边敲代码😖),换了个屏,小吉我现在是满血复活(啊哈哈哈),现在的我是看着新屏幕在写blog(着实很开兴🎉🎉🎉)
没想到,小吉我又讲了这么多的废话(太激动了,实在是抱歉~),从这里开始就要进入我们今天的学习了(前面的废话大家可以不看,但从这开始就要好好看了哦)。
今天我们要学习一种基础算法,也就是二叉搜索树,老规矩,在实现二叉搜索树之前,我们先来了解了解二叉搜索树是什么。
二叉搜索树的定义
二叉搜索树
1.树节点增加key属性,用来比较谁大谁小,key不可以重复
2.对于任意一个节点,它的key比左子树的key都大,同时也比右子树的key都小
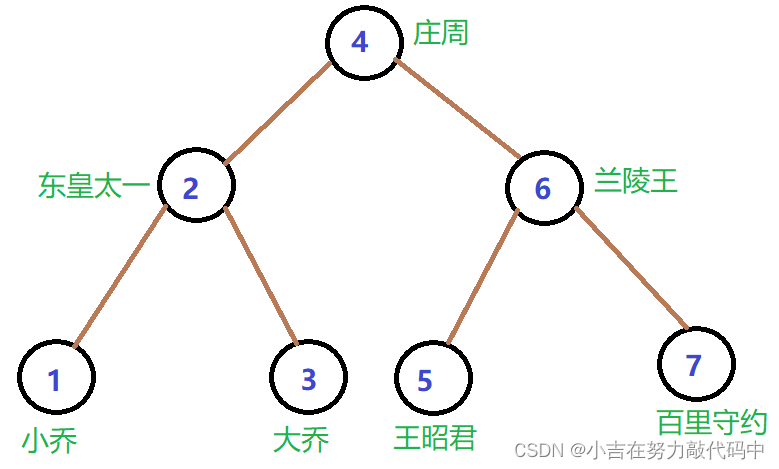
善解人意的小吉猜很多小可爱们看到这些概念都很难一下子就理解了,接下来小吉画一张图,方便大家理解(比起上面👆的概念,小吉认为下面的图比较重要)
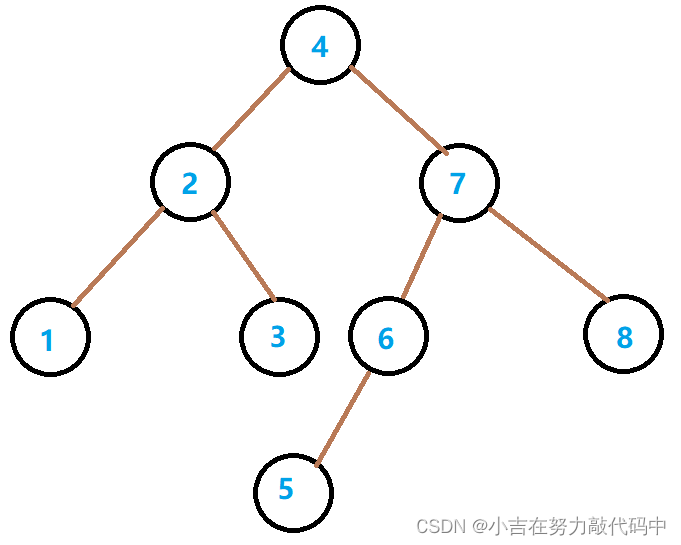
注:标的数值都是键值
最后,小吉来考考你们🧐,看看你们是否是真的了解了二叉搜索树,上图👆键值6的右子树的取值范围
(>6&&<7这个是答案哦~)
二叉搜索树的时间复杂度
(平均时间复杂度)O(logn) 对数时间
(最坏情况时间复杂度)O(n) 线性时间
(小吉不禁想到二分查找了,感觉二叉搜索树和二分查找有点莫名的相似,小吉我有出过和二分查找相关的博客,但没有总结过二分查找的知识点,看小可爱们的反馈吧,有需要小吉再出❤️)
二叉搜索树的实现大纲
get——查找键值对应的实值
min——查找最小键值对应的实值
max——查找最大键值对应的实值
put——存储键值和实值
successor——查找键值的前任(即前继节点)
predecessor——查找键值的后任(即后继节点)
deletednode——根据键值删除
范围查询:
myless——找<key的所有实值
mygreater——找>key的所有实值
mybetween——找>=key1且<=key2的所有实值
搭建基本框架
二叉搜索树节点类(不同之处:小吉我设置的节点有键值(起索引作用)和实值,所有元素都会根据元素的键值自动排序)
class BSTnode
{
public:
//初始化列表
BSTnode(int key,string value):_key(key),_value(value),_left(nullptr),_right(nullptr) {}
public:
int _key;//键值
string _value;//实值
BSTnode* _left;
BSTnode* _right;
};
实现二叉搜索树方法的类
class BSTTree
{
public:
BSTTree(BSTnode* root):_root(root) { }
public:
BSTnode* _root;//根节点
};
创建二叉搜索树(方便后期测试)
BSTnode* buildTree()
{
//创建根节点
BSTnode* root = new BSTnode(4, "庄周");
//创建左子树
root->_left = new BSTnode(2, "东皇太一");
root->_left->_left = new BSTnode(1, "小乔");
root->_left->_right = new BSTnode(3, "大乔");
//创建右子树
root->_right = new BSTnode(6, "兰陵王");
root->_right->_left = new BSTnode(5, "王昭君");
root->_right->_right = new BSTnode(7, "百里守约");
return root;
}
get——查找键值对应的实值
有两种实现方式,递归和非递归
思路:比较键值,以根节点为例,要找的键值比根节点的键值大,往右找;要找的键值比根节点的键值小,往左找;若相等,返回该节点的实值
递归实现,先实现一个递归查找的方法,再用get进行调用
string BSTTree::doGet(BSTnode* node, int key)
{
if (node == nullptr)
{
return "没找到";//没找到
}
if (node->_key<key)
{
return doGet(node->_right, key);
}
else if (node->_key>key)
{
return doGet(node->_left, key);
}
else
{
return node->_value;
}
}
string BSTTree:: get(int key)//查找键值对应的实值
{
return doGet(_root, key);
}
非递归实现
string BSTTree::get2(int key)
{
BSTnode* node = _root;
while (node != nullptr)
{
if (node->_key > key)
{
node = node->_left;
}
else if (node->_key < key)
{
node = node->_right;
}
else
{
return node->_value;
}
}
return "没找到";
}
min——查找最小键值对应的实值
思路:二叉搜索树的定义是对于一个任意节点它的左子树的一定比它小(针对键值_key而言),所以查找最小键值就要一直往左找,直到左子树为空,往左找可以分为递归和非递归两种方式
递归实现
string BSTTree::doMin(BSTnode* node)
{
if (node == nullptr)
{
return "二叉树中没有节点";
}
if (node->_left == nullptr)
{
return node->_value;
}
return doMin(node->_left);
}
string BSTTree::min()//查找最小键值对应的实值
{
return doMin(_root);
}
非递归实现
string BSTTree::min2()
{
if (_root == nullptr)
{
return "二叉树没有节点";
}
BSTnode* node = _root;
while (node->_left != nullptr)
{
node = node->_left;
}
return node->_value;
}
max——查找最大键值对应的实值
思路:和查找最小键值对应的实值思路差不多,要一直往右找,直到右子树为空
这里就只提供一种实现方式:非递归实现
string BSTTree::max()
{
if (_root == nullptr)
{
return "二叉树中没有节点";
}
BSTnode* p = _root;
while (p->_right != nullptr)
{
p = p->_right;
}
return p->_value;
}
put——存储键值和对应的实值
思路:分为两种情况,1)当提供的键值在树中存在,只用更新节点的实值即可 2)键值在树中不存在,就要新增节点(建立新的父子关系)
遍历二叉搜索树,查找键值是否存在,并在查找的过程中用指针记录父节点,找到直接更新即可;没找到新增节点,并建立父子关系
代码实现
void BSTTree::put(int key, string value)
{
BSTnode* node = _root;
BSTnode* parent = nullptr;
while (node != nullptr)
{
parent = node;
if (node->_key < key)
{
node = node->_right;
}
else if (node->_key > key)
{
node = node->_left;
}
else
{
//key找到了,更新
node->_value = value;
return;
}
}
//二叉树一开始就没有节点
if (parent == nullptr)
{
_root = new BSTnode(key, value);
return;
}
//key没有找到,新增
if (parent->_key > key)//parent为新增节点的父节点
{
parent->_left = new BSTnode(key, value);
}
else
{
parent->_right = new BSTnode(key, value);
}
}
小吉的这篇blog就先讲到这了,二叉搜索树还没有讲完,怕讲太多各位小伙伴们不能很好的吸收理解(其实一次性讲完小吉会很累的🤫)
学习的时间总是短暂的,这篇博客到这里就结束了,下一篇blog我们接着唠,期待一下小吉的下一篇blog吧,在小吉没有更新的日子里,希望大家不要忘了小吉哦❤️,也别忘了好好学习数据结构和算法(共勉💪)
最后的最后,创作不易,还望各位baby们多多支持🌹🌹🌹
(如有错,还望各位大大们多多指导😘)