题意

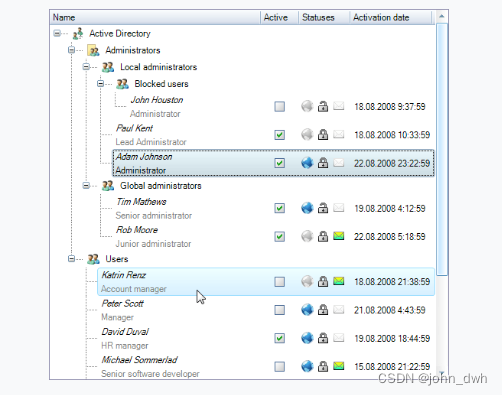
多组数据，每组输入两个数a，b，求区间a，b内的素数个数。

其中 $1 \leqslant a \leqslant b < 2^{31}, b - a \leqslant 100000$ .

思路

首先我们看到数据范围就能知道，传统的质数筛肯定行不通了

(令 $N=2^{31}$ ）

那么有个经典的方法就是筛出 $\sqrt N$ 内的质数，用 $[2,\sqrt N]$ 内的质数把 $[1,N]$ 内的所有合数筛掉

也就是说我们只需用欧拉筛筛出 $[2,2^{16}]$ 区间内的质数即可

那么对于区间 $[l,r]$ 内的素数，自然是用 $[2,\sqrt r]$ 内的质数把 $[1,r]$ 内的所有合数筛掉.

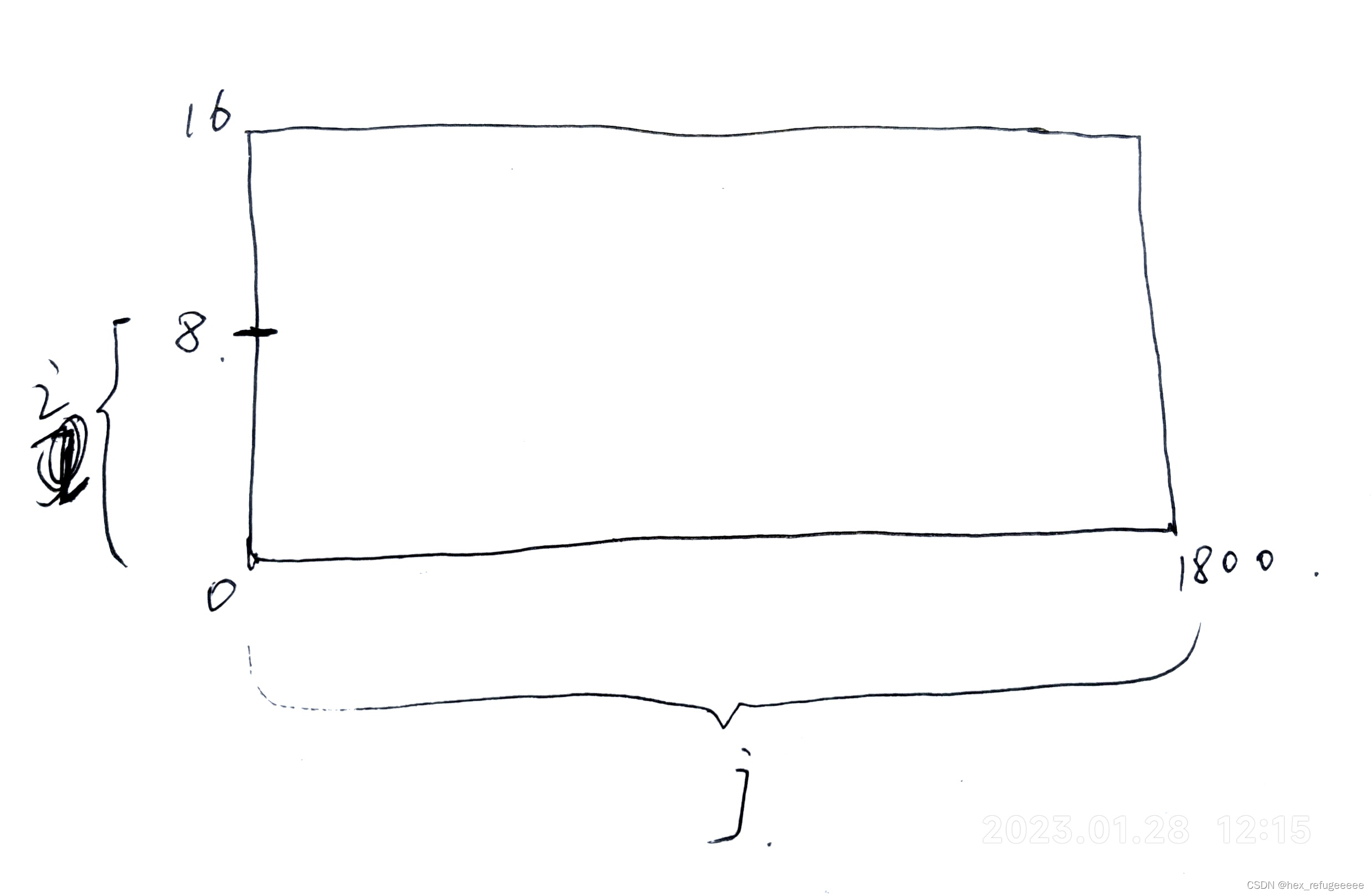
在筛合数的时候我们可以对左区间进行一定的优化处理：

用质数 $p_{i}$ 来筛合数时的左区间选择可以是第一个能被质数 $p_{i}$ 筛掉的质数即 $p_{i}\times p_{i}$ (到用 $p_{i}$ 筛时 $2\times p_{i},3\times p_{i}.....$ 都会在之前被其他质数筛掉)，另外要保证的一点时筛的左区间要 $\geqslant l$ ，所以可以是 $[\frac{l}{p_{i}}]\times p_{i}$ ，那么左区间的选择就是 $\max (p_{i}\times p_{i}, [\frac{l}{p_{i}}]\times p_{i})$ .

这就是利用了埃氏筛的思想来处理区间

还有一个值得注意的点， $l,r$ 可能非常大，所以在处理的时候我们可以把区间 $[l,r]$ 映射到 $[0, r-l]$

Solution

Status	Accepted
Time	62ms
Memory	888kB
Length	906
Lang	C++ 17 (g++ 7.5.0)

#include <bits/stdc++.h>
using namespace std;
const int N = (1 << 16) + 10;
bool vis[N], vis1[100010];
int p[N], cnt;

void get_primes(){
  for (int i = 2; i < N; i++) {
    if (!vis[i]) p[cnt++] = i;
    for (int j = 0; p[j] < N / i; j++){
      vis[i * p[j]] = true;
      if (i % p[j] == 0) break;
    }
  }
}

int segment_sieve(long long a, long long b){
  memset(vis1, 0, sizeof vis1);
  if(a == 1) a++;

  int ans = 0;
  for(int i = 0; p[i] <= b / p[i]; i++){
    long long st = max(1LL * p[i] * p[i], a / p[i] * p[i]);
    for(long long j = st; j <= b; j += p[i]){
       vis1[j - a] = 1;
    }
  }

  for(int i = 0; i <= b - a; i++)
    if(!vis1[i])
      ans++;
      
  return ans;
}

signed main(){
  get_primes();
  int t;
  scanf("%d", &t);
  for(int k = 1; k <= t; k++){
    long long a, b;
    scanf("%lld%lld", &a, &b);
    printf("Case %d: %d\n", k, segment_sieve(a, b));
  }
  return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/181721.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！