前言

二叉树是一种重要的数据结构，其中每个节点最多有两个子节点：左子节点和右子节点。它常用于实现搜索算法、排序算法、数据存储和图形表示等。二叉树具有递归性，可以通过遍历算法（如前序、中序、后序和层次遍历）来访问其节点。学习和理解二叉树对于掌握更复杂的数据结构和算法至关重要。

堆

1.1 二叉树的概念

二叉树（Binary Tree）是一种特殊的树形数据结构，它的每个节点最多有两个子节点，通常被称为左子节点和右子节点，二叉树的子树有左右之分，其次序不能任意颠倒。

1. 根节点（Root Node）：二叉树的起始节点，它没有父节点，但可能有左子节点和右子节点。
2. 父节点（Parent Node）：对于每个节点(除根节点之外的节点)，都有父节点，是一个具有子节点的节点。
3. 左子节点（Left Child）：对于每个节点，其左下方的节点称为其左子节点。
4. 右子节点（Right Child）：对于每个节点，其右下方的节点称为其右子节点。
5. 叶子节点（Leaf Node）：没有子节点的节点称为叶子节点。
6. 非叶子节点（Non-Leaf Node）：除了叶子节点以外的节点都称为非叶子节点。
7. 度（Degree）：节点的度是指该节点的子节点数量。在二叉树中，节点的度最大为2。
8. 深度（Depth）：从根节点到最远叶子节点的最长路径上的节点数称为二叉树的深度。
9. 高度（Height）：对于任意节点n，n的高度为从n到一片树叶的最长路径上的节点数。所有树叶的高度为0，根节点的高度就是树的高度。

1.2 满二叉树和完美二叉树

满二叉树（Full Binary Tree）：除了叶子节点外，每一个节点都有左右两个子节点的二叉树称为满二叉树。

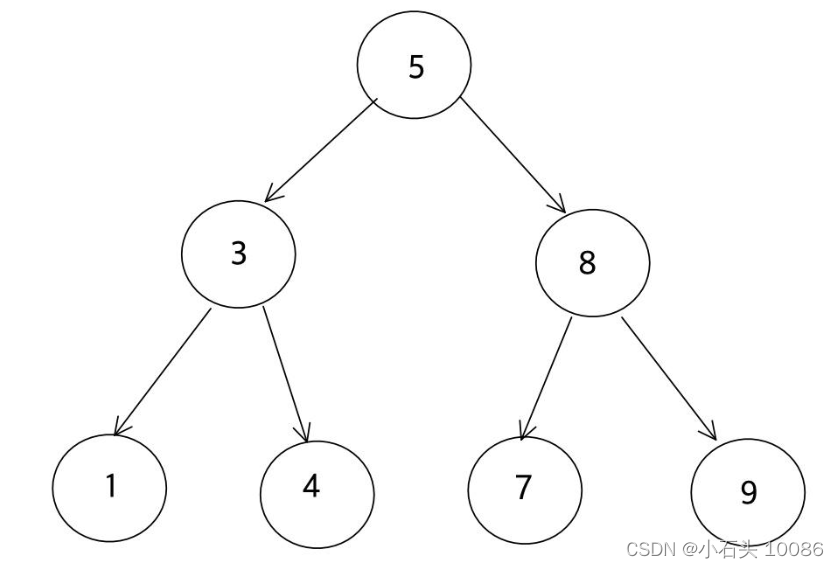
完全二叉树（Complete BinaryTree）：完全二叉树从根结点到倒数第二层满足完美二叉树，最后一层可以不完全填充，其叶子结点必须靠左对齐，且不能有短，最后一层最少可以只有一个。

这不是一个完美二叉树

1.3 堆的概念

堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵 完全二叉树的 数组对象。 堆是非线性数据结构，相当于一维数组，有两个直接后继。

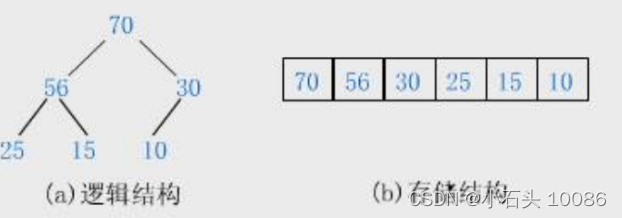
• 大堆：父节点一定比子节点大，但是兄弟节点之间，不存在大小关系，堆的根节点是整个堆中最大的数
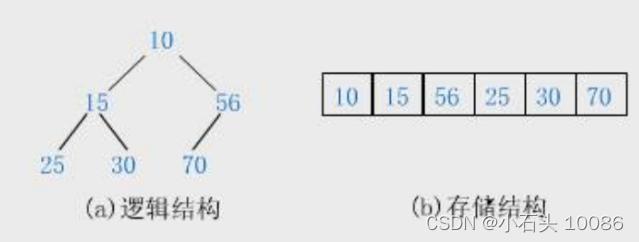
• 小堆：父节点一定比子节点小，但是兄弟节点之间，不存在大小关系，堆的根节点是整个堆中最小的数

堆的父亲节点的下标和子节点的下标可以进行相互运算：

• Parent = (Chlid - 1) / 2
• Chlid = Parent / 2 - 1

1.4 堆的性质

• 堆是完美二叉树构成。

大堆：

小堆：

1.4 堆的实现

1.4.1堆的向上调整算法

给定一个数组，且这个堆是一个小堆，逻辑上看作是一种完美二叉树，需要传两个参数，一个数组，一个就是插入位置的节点在数组中的下标。

• 在数组的最后插入数据，开始进行向上调整算法。
• 如果这个节点小于他的父亲节点，那就进行交换。
• 如果这个节点大于他的父亲节点，那就结束向上调整。

这里给一组数据进行交换

int a[] = {10,15,56,25,30,70,5};

堆的向上调整算法代码实现：

void Swap(HPDataType* x,HPDataType* y)
{
	HPDataType tmp = *x;
	*x = *y;
	*y = tmp;
}
void AdjustUp(HPDataType* a, int child)
{
	int Parent = (child- 1) / 2;
	while (child> 0)
	{
		if (a[Parent] > a[child])
		{
			Swap(&a[Parent], &a[child]);
			child = Parent;
			Parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

1.4.1堆的向下调整算法

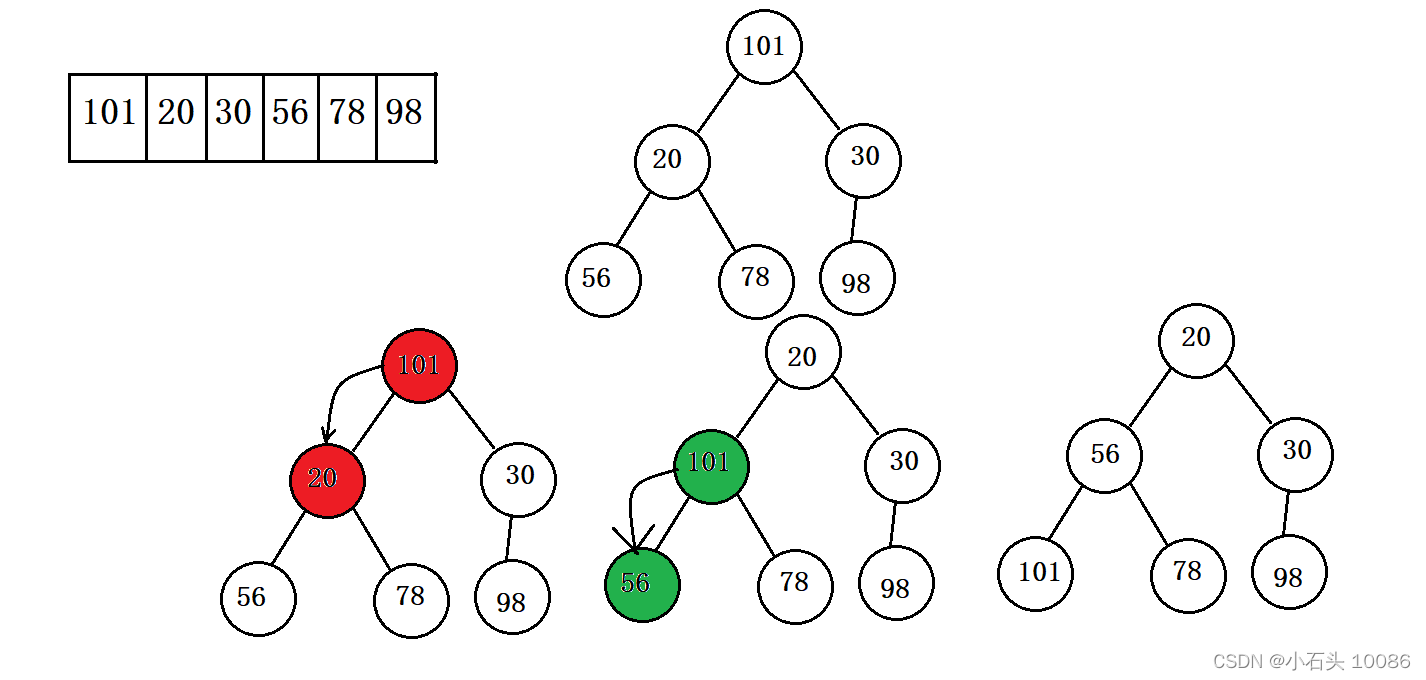
给定一个数组，且这个堆是一个小堆，逻辑上看作是一种完美二叉树。然后我们从根节点开始向下调整，向下调整算法有一个前提：左右子树必须是一个堆，才能进行调整。然后计算出这个根节点的两个孩子节点，进行比较，哪个小，让其与根节点进行比较。这里需要传三个参数，第一个数组，第二个是数组的个数，第三个是根节点的下标。

• 如果根节点大于孩子节点，那就进行交换。
• 如果根节点小于孩子节点，就停止交换。

这里给一组数据进行交换

int a[]= {}

堆的向下调整算法代码实现：

void Swap(HPDataType* x,HPDataType* y)
{
	HPDataType tmp = *x;
	*x = *y;
	*y = tmp;
}
void AdjustDown(HPDataType* a, int n, int Parent)
{
	// 这里可以使用假设法
	int child = Parent * 2 + 1;
	while (child < n)
	{
		// 假设法这个位置需要进行判断是否是小的哪个孩子，不是则需要进行更新
		if (a[child] > a[child + 1] && child + 1 < n)
		{
			child += 1;
		}
		if (a[Parent] > a[child])
		{
			Swap(&a[Parent], &a[child]);
			Parent = child;
			child = Parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

1.4.1堆的接口实现

• 堆的初始化(HeapInit)：用于初始化堆结构，为堆的后续操作做好准备。
• 堆的销毁(HeapDestroy)：释放堆占用的资源，通常涉及删除堆中的所有元素和释放内存。
• 堆的插入(HeapPush)：向堆中插入一个新元素，并保持堆的性质（大堆或小堆）。
• 堆的删除(HeapPop)：删除堆顶数据，将堆顶数据和堆尾数据进行交换，并保持堆的性质（大堆或小堆）。
• 获取堆顶数据(HeapTop)：获取堆顶数据。
• 堆的判空(HeapEmpty)：判断堆是否是空。
• 堆的数据个数(HeapSize)：计算堆中的数据个数。

1.4.1.1堆的初始化

对于堆的这个结构体来说，可以给_a开空间，也可以不开，一会儿进行push的时候，会进行判断，所以就可以制空，以防止成为野指针。对于size，可以给-1，这样就刚刚好和下标对上了。

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;
	int _size;    // 堆顶的下一个位置的下标
	int _capacity;// 堆的空间
}Heap;
// 堆的初始化
void HeapInit(Heap* hp)
{
	assert(hp);

	hp->_a = NULL;
	hp->_capacity = hp->_size = 0;
}

1.4.1.2堆的销毁

void HeapDestroy(Heap* php)
{
	assert(php);
	free(php->_a);
	php->_a = NULL;
	php->_size = php->_capacity = 0;
}

1.4.1.3堆的插入

这里插入数据，需要插入到这个数组的最后一个位置，然后进行向上调整算法，让他始终保持这个小堆（大堆）。

void HeapPush(Heap* php,HPDataType x)
{
	assert(php);
	if (php->_capacity == php->_size)
	{
		int newcapacity = php->_capacity == 0 ? 4 : php->_capacity * 2;
		HPDataType* new_a = (HPDataType*)realloc(php->_a,newcapacity*sizeof(HPDataType));
		if (new_a == NULL)
		{
			perror("HeapPush()::realloc() fail!!");
			return;
		}
		php->_capacity = newcapacity ;
		php->_a = new_a;
	}
	php->_a[php->_size++] = x;
	AdjustUp(php->_a, hp->_size - 1);
}

1.4.1.4堆的删除

需要将堆中最后一个节点于整个堆的根节点进行交换，交换完成之后，直接删除最后一个下标的位置，在进行向下调整。

void HeapPop(Heap* php)
{
	assert(php && php->_size > 0);
	Swap(&php->_a[0],&php->_a[php->_size - 1]);
	php->_size--;
	AdjustDown(php->_a, php->_size, 0);
}

1.4.1.4堆的判空

因为结构体中的size就是用来记录堆的数据个数的，所以可以直接判断这个数是否等于0。

int HeapEmpty(Heap* php)
{
	assert(php);
	 return php->_size == 0;
}

1.4.1.4 获取堆的数据个数

结构体中的size就是用来计数的，所以会方便很多

void HeapSize(Heap* php)
{
	assert(php);
	return php->_size;
}