目录

详细布置：

1. 491. 非递减子序列

2. 46. 全排列

3. 47. 全排列 II

---

详细布置：

1. 491. 非递减子序列

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

建议：本题和大家刚做过的 90.子集II 非常像，但又很不一样，很容易掉坑里。

本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。

所以不能使用之前的去重逻辑！

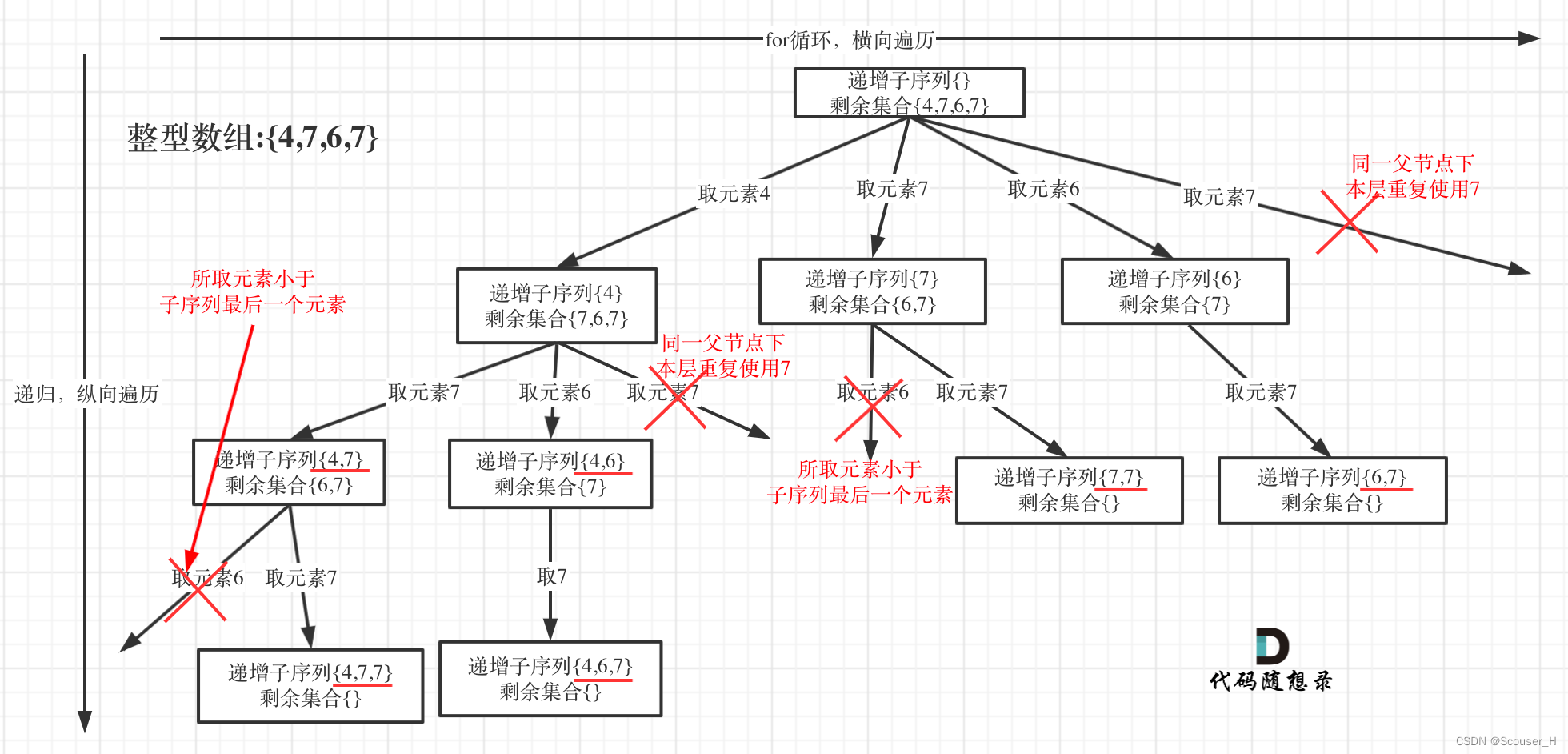
本题给出的示例，还是一个有序数组 [4, 6, 7, 7]，这更容易误导大家按照排序的思路去做了。

为了有鲜明的对比，我用[4, 7, 6, 7]这个数组来举例，抽象为树形结构如图：

class Solution:
    def findSubsequences(self, nums):
        result = []
        path = []
        self.backtracking(nums, 0, path, result)
        return result
    
    def backtracking(self, nums, startIndex, path, result):
        if len(path) > 1:
            result.append(path[:])  # 注意要使用切片将当前路径的副本加入结果集
            # 注意这里不要加return，要取树上的节点
        
        uset = set()  # 使用集合对本层元素进行去重
        for i in range(startIndex, len(nums)):
            if (path and nums[i] < path[-1]) or nums[i] in uset:
                continue
            
            uset.add(nums[i])  # 记录这个元素在本层用过了，本层后面不能再用了
            path.append(nums[i])
            self.backtracking(nums, i + 1, path, result)
            path.pop()

---

2. 46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

建议：本题重点感受一下，排列问题 与 组合问题，组合总和，子集问题的区别。 为什么排列问题不用 startIndex

class Solution:
    def permute(self, nums):
        result = []
        self.backtracking(nums, [], [False] * len(nums), result)
        return result

    def backtracking(self, nums, path, used, result):
        if len(path) == len(nums):
            result.append(path[:])
            return
        for i in range(len(nums)):
            if used[i]:
                continue
            used[i] = True
            path.append(nums[i])
            self.backtracking(nums, path, used, result)
            path.pop()
            used[i] = False

---

3. 47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

建议：本题 就是我们讲过的 40.组合总和II 去重逻辑 和 46.全排列 的结合，可以先自己做一下，然后重点看一下 文章中 我讲的拓展内容。 used[i - 1] == true 也行，used[i - 1] == false 也行

还要强调的是去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

class Solution:
    def permuteUnique(self, nums):
        nums.sort()  # 排序
        result = []
        self.backtracking(nums, [], [False] * len(nums), result)
        return result

    def backtracking(self, nums, path, used, result):
        if len(path) == len(nums):
            result.append(path[:])
            return
        for i in range(len(nums)):
            if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1]) or used[i]:
                continue
            used[i] = True
            path.append(nums[i])
            self.backtracking(nums, path, used, result)
            path.pop()
            used[i] = False