T3-加密通信

news2024/11/29 22:43:05

T3-加密通信

题目描述

在一次军事演习中，小凯担任通信兵，负责解密传来的信息。他会收到一份 nn 的数字表（仅包含 0-9 共 10 种数码），和一份 mm 的字母表（仅包含 A-Z、a-z 共 52 种字符）。数字表被称为解密卡，字母表被称为加密卡。规定如下名词：

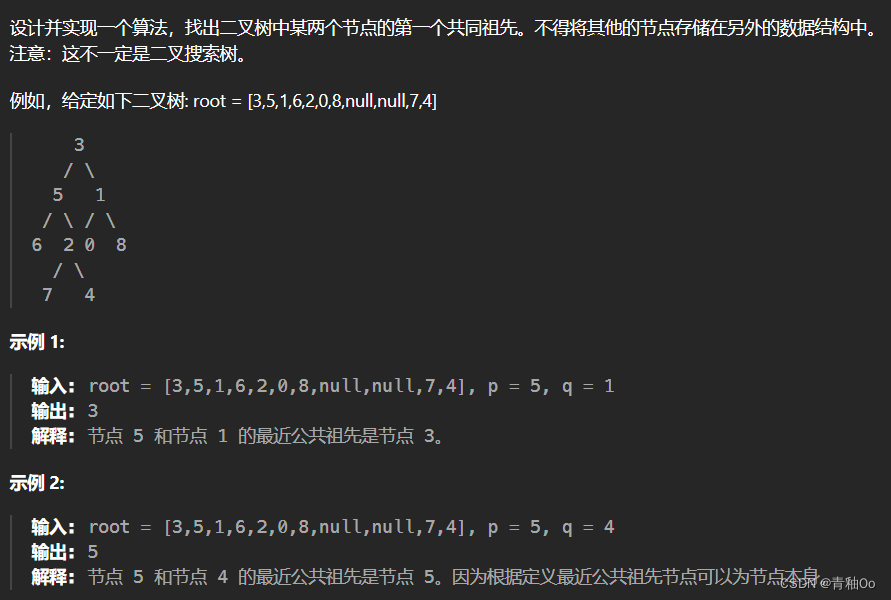
1.覆盖区域：将数字表和字母表对齐，使得数字表在上，字母表在下，数字与字母一一对应，如果数字表的 1 行 1 列对应字母表的 x 行 y 列，那么数字表的 1+k 行 1+k 列对应字母表的 x+k 行 y+k 列，此时覆盖区域为字母表以 x 行 y 列为左上角、x+n-1 行 y+n-1 列为右下角的正方形范围。简单来说，根据图片显示，若数字表的左上角盖在了 2 行 2 列的位置，则数字表会覆盖（2，2）到（3，3）这片区域。
2.有效区域：称某字母和其在字母表的顺序数字为互相对应，字母 A 和 a 是第 1 个字母、字母 I 和 i 是第 9 个字母，那么 A、a 和 1 对应，I、i 和 9 对应，以此类推。如果覆盖区域的四个顶点字母恰好和原始数字表的四个顶点数字互相对应，那么这个覆盖区域称之为有效区域。
3.数字关联：0 和任何字母关联，1 不能和任何字母关联，2-9 中的质数和大写字母关联， 2-9 中的合数和小写字母关联。若关联成功，则提取出来作为密码的一部分，如上图中 2 是质数，需关联大写字母，2 对应的是 B，关联成功；3 是质数，需关联大写字母，3 对应的 c 关联失败；4 是合数，需关联小写字母，而 4 对应的是 D，关联失败。因此上述图中，本次覆盖只关联成功一次，提取出一个密码 B。
1. 解密数字表：大小为 n*n，可以由原始数字表顺时针旋转若干次 90°得到。
5.区域解密：有效区域和解密数字表对齐，从左到右从上到下，将和解密数字表中对应位置数字恰好关联的字母提取出来，构成字符串。
一次解密操作包含以下步骤：首先从左到右从上到下找出所有有效区域，依次进行解密。对于每个有效区域首先用原始数字表进行 1 次区域解密，然后根据当前有效区域的顶点大写字母数量 x，额外进行 x 次区域解密（如图示中四个顶点有两个大写字母，因此需旋转两次），第 i 次解密时将原始数字表顺时针旋转 i*90°后作为解密数字表再进行区域解密。最后将所有区域解密的字符串按序连接，构成最终的解密字符串。你需要帮助小凯完成解密工作。

输入格式

共 n+m+1 行，第 1 行两个正整数 n 和 m，分别代表数字表和字母表的大小；第 2 至 n+1 行分别有连续的 n 个数码字符，代表数字表的内容；第 n+2 至 n+m+1 行分别有连续的 m 个字母字符，代表字母表的内容。

输出格式

仅一行一个字符串，代表解密后的答案。如果答案为空串，你需要输出“No solution”

样例 #1

样例输入 #1

2 3  
11  
13  
AAB  
ACB  
BzB

样例输出 #1

CAAAC

样例 #2

样例输入 #2

3 4  
101  
245  
313  
DABa  
AFab  
Fcdc  
cdcD

样例输出 #2

BFaABabFFcAFcd

提示

对于 30%的数据，保证输入的 m<=10。在前 30%中有 10%的数据，保证数字表中仅含有 0 和 1。
对于 70%的数据，保证输入的 m<=50。在前 70%中有 30%的数据，保证字母表中仅含有小写字母。
对于 100%的数据，保证输入的 n<=m<=80。

解析
解题思路如下:

首先读入数字表和字母表的大小n和m,然后读入nn的数字表和mm的字母表。
从字母表的左上角开始,枚举所有可能的n*n的覆盖区域,对于每个覆盖区域:

a. 判断该覆盖区域是否为有效区域,即四个顶点字母是否和原始数字表的四个顶点数字互相对应。如果是有效区域,记录下该区域四个顶点中大写字母的数量x。

b. 如果是有效区域,则首先用原始数字表进行一次区域解密,然后根据x的值,将原始数字表顺时针旋转x*90度,再进行x次区域解密。

c. 区域解密时,将解密数字表与有效区域对齐,遍历解密数字表的每个位置,如果该位置的数字与对应的字母满足数字关联关系,则将该字母提取出来。
将所有有效区域解密得到的字符串按顺序拼接,即为最终的解密字符串。如果最终字符串为空,则输出"No solution"。

下面是C++的代码实现:

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;

int n, m;

// 判断覆盖区域是否为有效区域
bool validArea(const vector<vector<char>>& digit, const vector<vector<char>>& map, int& upperNums, int startI, int startJ) {
    vector<pair<int, int>> corners = {{0, 0}, {0, n - 1}, {n - 1, 0}, {n - 1, n - 1}};
    for (const auto& corner : corners) {
        int i = corner.first;
        int j = corner.second;
        if (digit[i][j] == '0') {
            continue;
        }
        if (isupper(map[startI + i][startJ + j])) upperNums++;
        char c = toupper(map[startI + i][startJ + j]);
        if ((digit[i][j] - '0') != (c - 'A' + 1)) {
            return false;
        }
    }
    return true;
}

// 顺时针旋转数字表90度
vector<vector<char>> rotateMatrix90(const vector<vector<char>>& matrix) {
    int n = matrix.size();
    vector<vector<char>> rotated(n, vector<char>(n));
    for(int i = 0; i < n; ++i) {
        for(int j = 0; j < n; ++j) {
            rotated[j][n - i - 1] = matrix[i][j];
        }
    }
    return rotated;
}

// 区域解密
void decode(const vector<vector<char>>& digit, const vector<vector<char>>& map, int times, int startI, int startJ, string& ans) {
    vector<vector<char>> rotate = digit;
    while(times--) {
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n; j++) {
                if(rotate[i][j] == '1') {
                    continue;
                } else if(rotate[i][j] == '0') {
                    ans += map[startI + i][startJ + j];
                } else if(rotate[i][j] == '2' || rotate[i][j] == '3' || rotate[i][j] == '5' || rotate[i][j] == '7') {
                    if(isupper(map[startI + i][startJ + j])) {
                        ans += map[startI + i][startJ + j];
                    }
                } else if(rotate[i][j] == '4' || rotate[i][j] == '6' || rotate[i][j] == '8' || rotate[i][j] == '9') {
                    if(islower(map[startI + i][startJ + j])){
                        ans += map[startI + i][startJ + j];
                    }
                }
            }
        }
        rotate = rotateMatrix90(rotate);
    }
}

int main() {
    cin >> n >> m;

    vector<vector<char>> digit(n, vector<char>(n));
    vector<vector<char>> map(m, vector<char>(m));

    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            cin >> digit[i][j];
        }
    }

    for(int i = 0; i < m; i++) {
        for(int j = 0; j < m; j++) {
            cin >> map[i][j];
        }
    }

    string ans;
    for(int i = 0; i < m - n + 1; i++) {
        for(int j = 0; j < m - n + 1; j++) {
            int upperNums = 0;
            if(validArea(digit, map, upperNums, i, j)) {
                decode(digit, map, upperNums + 1, i, j, ans);
            }
        }
    }

    if(ans.size() == 0){
        cout << "No solution";
        return 0;
    }
    cout << ans << endl;
    return 0;
}