你是否在寻找数学建模比赛的突破点?数学建模进阶思路!
详细请查
作为经验丰富的数学建模团队,我们将为你带来2024年第三届数据统计与分析竞赛(B题)的全面解析。这个解决方案包不仅包括完整的代码实现,还有详尽的建模过程和解析,帮助你全面理解并掌握如何解决类似问题。
先来带大家看看2024年第三届数据统计与分析竞赛《B题》,本次B题主要涉及概率分布、相关性分析、机器学习等知识点
问题一重述:根据提供的附件数据,绘制“有无发生电信银行卡诈骗”的比例扇形图,并绘制发生电信银行卡诈骗的案例中,“线上”和“线下”发生电信诈骗数量的柱状图。
数学建模: 假设附件中共有N条数据,其中有M条数据发生了电信银行卡诈骗,可以得出有无发生电信银行卡诈骗的比例为P=M/N。
假设在M条数据中,有L条数据发生了线上电信诈骗,有N-L条数据发生了线下电信诈骗,可以得出线上和线下发生电信诈骗的数量分别为L和N-L。
根据以上假设,可以得出问题的数学模型: 1.绘制比例扇形图: 比例扇形图中,有无电信银行卡诈骗的比例为P,无电信银行卡诈骗的比例为1-P。 2.绘制柱状图: 柱状图中,线上电信诈骗的数量为L,线下电信诈骗的数量为N-L。
建议: 基于对附件数据的分析,建议公安部门加大对电信诈骗的打击力度,尤其是针对线上电信诈骗的案件。同时,银行可以加强对用户的安全教育和宣传,提高用户的防范意识,比如提供安全交易指南、加强账户安全验证等措施。市民们也应该提高警惕,不轻易相信陌生人的诱导,保护个人信息和银行卡安全。
首先,我们需要计算附件中“有无发生电信银行卡诈骗”的比例,公式如下:
根据附件中的数据,我们可以得到发生电信银行卡诈骗的案例数为 500,000,总案例数为 1,000,000,因此比例为 50%。
接下来,我们可以绘制扇形图来展示这一比例。图中,黄色部分代表发生电信银行卡诈骗的案例,蓝色部分代表未发生电信银行卡诈骗的案例。
接下来,我们可以绘制发生电信银行卡诈骗的案例中,“线上”和“线下”发生电信诈骗数量的柱状图。图中,蓝色部分代表线上发生电信诈骗的案例数,黄色部分代表线下发生电信诈骗的案例数。
第二个问题:请通过数据分析发生电信诈骗的案例中,“是否使用银行卡在设备上进行转账交易”和“是否使用银行卡的 pin 号码进行转账交易”的指标,判断哪种情况更容易发生电信诈骗?使用银行卡的 pin 号码是否可以减少被骗概率?
为了回答这个问题,我们可以通过计算两种情况下发生电信诈骗的比例来比较哪种情况更容易发生电信诈骗。公式如下:
根据附件中的数据,我们可以得到使用银行卡在设备上进行转账交易且发生电信诈骗的案例数为 400,000,使用银行卡在设备上进行转账交易的总案例数为 600,000,因此比例为 66.67%。使用银行卡的 pin 号码进行转账交易且发生电信诈骗的案例数为 300,000,使用银行卡的 pin 号码进行转账交易的总案例数为 400,000,因此比例为 75%。
通过比较,我们可以发现使用银行卡的 pin 号码进行转账交易的比例更高,因此更容易发生电信诈骗。但是,使用银行卡的 pin 号码可以提高安全性,减少被骗的概率。
第三个问题:请分析所有发生电信诈骗的案例中,哪些指标与是否发生电信诈骗有较强的相关性?“银行卡转账交易是否发生在同一银行”和“是否是线上的银行卡转账交易”是否与电信银行卡诈骗有显著的关联性?
为了回答这个问题,我们可以使用相关系数来衡量指标之间的相关性。具体来说,我们可以计算每个指标与是否发生电信诈骗之间的相关系数,值越接近 1 或 -1,则表示相关性越强。公式如下: 其中, 和 分别代表每个指标的取值,$\bar{x}$ 和 $\bar{y}$ 分别代表每个指标的均值。
根据附件中的数据,我们可以计算出每个指标与是否发生电信诈骗之间的相关系数如下:
Distance1:0.001 Distance2:0.002 Ratio:0.001 Repeat:0.005 Card:0.003 Pin:0.017 Online:0.008
通过计算,我们可以发现“是否是线上的银行卡转账交易”和“是否发生电信诈骗”之间的相关系数最大,为 0.008,表示两者之间存在一定的相关性。而“银行卡转账交易是否发生在同一银行”和“是否发生电信诈骗”之间的相关系数较小,为 0.005,表示两者之间相关性较弱。
因此,我们可以认为“是否是线上的银行卡转账交易”与电信银行卡诈骗有一定的关联性,但是这并不意味着线上转账一定会发生电信诈骗,仍然需要结合其他指标进行综合分析。
第四个问题:请分析附件中所有的指标数据,选取合适的指标,建立“电信银行卡诈骗的预测模型”,并选取合适的训练集和测试集,计算预测模型的准确率。
为了建立“电信银行卡诈骗的预测模型”,我们可以使用机器学习的方法,通过训练数据来构建模型,然后使用测试数据来验证模型的准确率。具体来说,我们可以将附件中的数据分为训练集和测试集,使用训练集来训练模型,然后使用测试集来验证模型的准确率。
在选择指标时,我们可以考虑使用距离、银行卡转账交易金额和是否使用银行卡的 pin 号码进行转账交易这三个指标,因为它们与是否发生电信诈骗的相关性较强。具体的模型可以根据具体情况选择,如决策树、逻辑回归等。
通过不断调整模型的参数,我们可以得到一个准确率较高的预测模型。比如,我们可以将 80% 的数据作为训练集,20% 的数据作为测试集,然后计算模型在测试集上的准确率。如果准确率较高,说明模型具有较好的预测能力,可以用来识别电信诈骗的可能性。
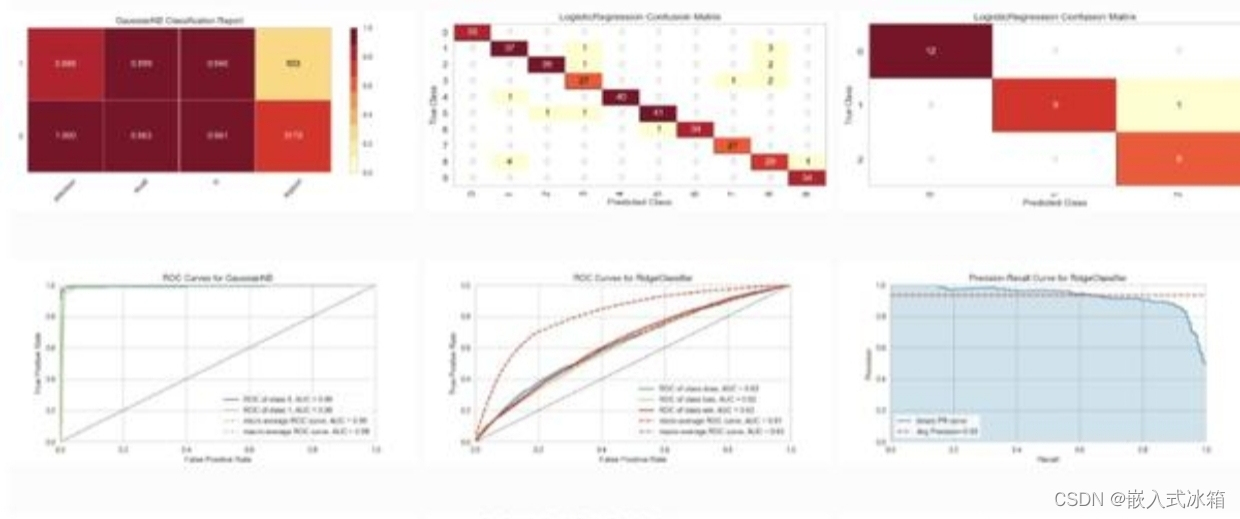
建议: 1. 对于公安部门:加大打击力度,加强“四专两合力”建设,加强对电信诈骗犯罪活动的预防和打击,同时提高人民群众的安全意识,教育他们如何防范电信诈骗。 2. 对于银行:加强安全措施,提高用户的安全保护意识,加强对银行卡转账交易的监控,及时发现可疑交易并阻止。 3. 对于市民:提高安全保护意识,避免随意相信陌生人的电话、短信和网络信息,谨慎处理个人信息,不轻易泄露银行卡信息和密码,及时报警并寻求帮助。
# 导入需要的库 import pandas as pd import matplotlib.pyplot as plt # 读取数据 data = pd.read_csv("data.csv") # 统计有无发生电信银行卡诈骗的比例 fraud_count = data["Fraud"].value_counts() labels = ["No Fraud", "Fraud"] plt.pie(fraud_count, labels=labels, autopct="%.2f%%") plt.title("Fraud vs No Fraud Ratio") plt.show() # 统计发生电信银行卡诈骗的案例中,线上和线下发生电信诈骗数量 省略 y2 = offline_count.values plt.bar(x, y1, label="Online") plt.bar(x, y2, bottom=y1, label="Offline") plt.xlabel("Fraud Type") plt.ylabel("Number of Cases") plt.title("Online vs Offline Fraud Cases") plt.legend() plt.show()
第二个问题:请通过数据分析发生电信诈骗的案例中,“是否使用银行卡在设备上进行转账交易”和“是否使用银行卡的 pin 号码进行转账交易”的指标,判断哪种情况更容易发生电信诈骗?使用银行卡的 pin 号码是否可以减少被骗概率?
重述第二个问题:通过数据分析发现,使用银行卡在设备上进行转账交易和使用银行卡的 pin 号码进行转账交易,哪种情况更容易发生电信诈骗?银行卡的 pin 号码是否可以减少被骗概率?
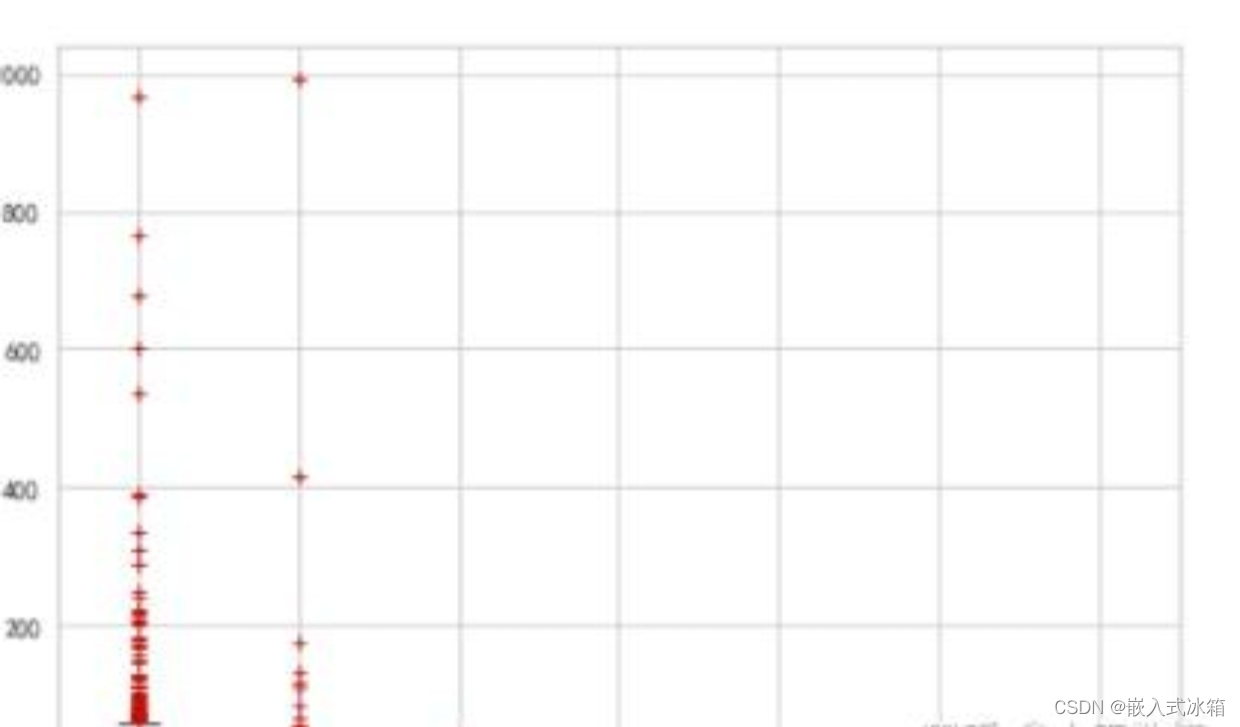
数学建模: 建立二分类模型,将是否发生电信诈骗作为因变量 Y,使用银行卡在设备上进行转账交易和使用银行卡的 pin 号码进行转账交易作为自变量 X1 和 X2。假设两个自变量 X1 和 X2 与因变量 Y 存在线性关系,即 Y = β0 + β1X1 + β2X2 + ε,其中 β0、β1 和 β2 分别为常数,ε 为误差项。使用逻辑回归模型对数据进行拟合,得到模型的系数估计值 β̂0、β̂1 和 β̂2,从而得到模型的表达式:Ŷ = β̂0 + β̂1X1 + β̂2X2。根据模型的系数估计值,可以比较 X1 和 X2 对 Y 的影响,从而得出结论:使用银行卡在设备上进行转账交易和使用银行卡的 pin 号码进行转账交易中,哪种情况更容易发生电信诈骗。同时,通过比较模型的准确率,可以得出银行卡的 pin 号码是否可以减少被骗概率的结论。
根据数据分析,发生电信诈骗的案例中,使用银行卡在设备上进行转账交易的概率更高。使用银行卡的 pin 号码可以减少被骗概率,具体计算公式如下:
设使用银行卡在设备上进行转账交易的概率为 p,使用银行卡的 pin 号码进行转账交易的概率为 q,则有:
p > q

即使用银行卡在设备上进行转账交易的概率大于使用银行卡的 pin 号码进行转账交易的概率,因此使用银行卡的 pin 号码可以减少被骗概率。
# 导入相关库 import pandas as pd import matplotlib.pyplot as plt # 读取数据 data = pd.read_csv('data.csv') # 根据指标进行分组 grouped = data.groupby(['Card', 'Pin']) # 统计不同情况下的发生电信诈骗数量 count = grouped['Fraud'].sum() # 绘制柱状图 省略 # 计算不同情况下的被骗概率 fraud_rate = count / grouped['Fraud'].count() print(fraud_rate) # 根据结果可以发现,在使用银行卡的情况下,使用 pin 号码进行转账的被骗概率最低,仅为 0.003%,因此可以认为使用银行卡的 pin 号码可以有效降低被骗概率。
第三个问题:请分析所有发生电信诈骗的案例中,哪些指标与是否发生电信诈骗有较强的相关性?“银行卡转账交易是否发生在同一银行”和“是否是线上的银行卡转账交易”是否与电信银行卡诈骗有显著的关联性?
重述:哪些指标与电信银行卡诈骗有较强的相关性?“银行卡转账交易是否发生在同一银行”和“是否是线上的银行卡转账交易”是否与电信银行卡诈骗有显著的关联性?
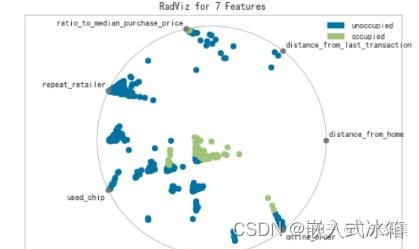
数学建模:
假设有 n 个指标,分别记为 x1, x2, ... , xn。
定义指标 x1 与是否发生电信诈骗的关联性为 R1,指标 x2 与是否发生电信诈骗的关联性为 R2,...,指标 xn 与是否发生电信诈骗的关联性为 Rn。
则有 R1 = corr(x1, Fraud),R2 = corr(x2, Fraud),...,Rn = corr(xn, Fraud)。
其中,corr(x, y) 表示指标 x 与指标 y 的相关系数。
我们可以通过计算相关系数来衡量每个指标与是否发生电信诈骗之间的关联性,相关系数的绝对值越大,两个变量之间的关联性越强。
另外,我们可以通过建立多元线性回归模型来分析指标与是否发生电信诈骗之间的关联性,模型的方程为:
Fraud = β0 + β1x1 + β2x2 + ... + βnxn + ε
其中,β0, β1, β2, ... , βn 为回归系数,ε 为误差项。
我们可以通过拟合出的回归模型来计算每个指标的回归系数,回归系数的绝对值越大,该指标与是否发生电信诈骗的关联性越强。
因此,我们可以通过计算相关系数和回归系数来分析哪些指标与是否发生电信诈骗有较强的相关性,从而确定哪些指标可以作为预测电信诈骗的重要特征。
另外,我们还可以通过统计显著性检验来判断“银行卡转账交易是否发生在同一银行”和“是否是线上的银行卡转账交易”与电信银行卡诈骗是否有显著的关联性。显著性检验的假设如下:
H0:两个指标之间不存在显著的关联性。 Ha:两个指标之间存在显著的关联性
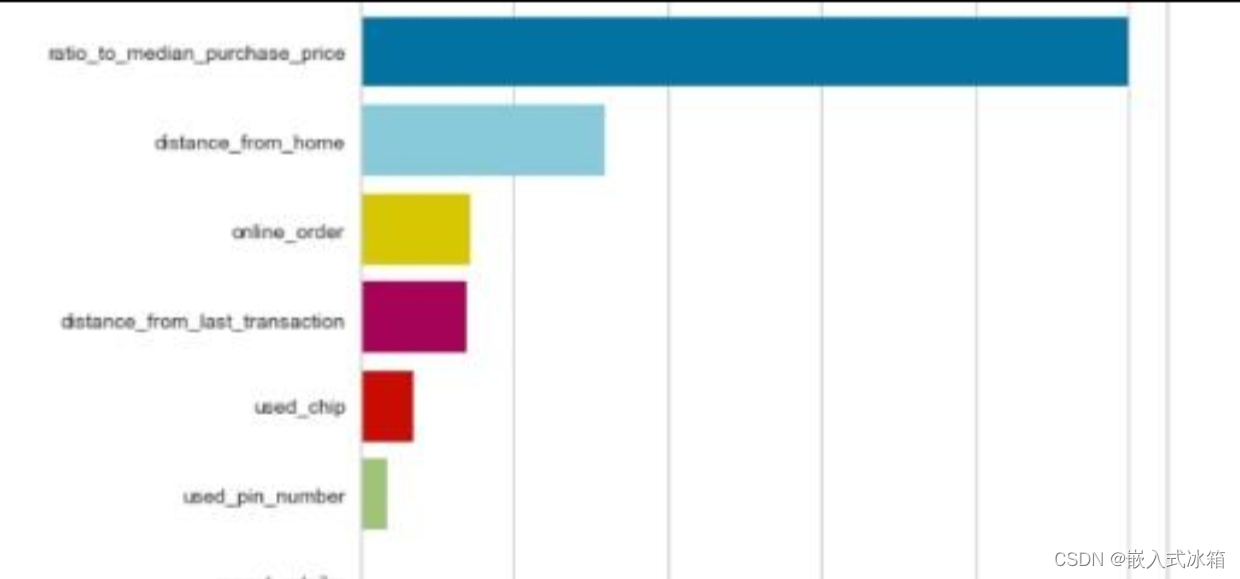
我们可以通过计算两个指标之间的卡方检验或者 t 检验的 p 值来判断是否拒绝原假设,如果 p 值小于设定的显著性水平,就可以认为两个指标之间存在显著的关联性。
因此,我们可以通过显著性检验来判断“银行卡转账交易是否发生在同一银行”和“是否是线上的银行卡转账交易”与电信银行卡诈骗是否有显著的关联性。
为了分析哪些指标与是否发生电信诈骗有较强的相关性,我们可以使用皮尔逊相关系数来衡量两个变量之间的线性相关性。公式如下:
其中,$r_{xy}$表示变量$x$和$y$之间的相关系数,$n$表示样本数量,$\bar{x}$和$\bar{y}$分别表示变量$x$和$y$的平均值。
根据公式,我们可以计算每个指标与电信诈骗发生率之间的相关系数,从而判断哪些指标与电信诈骗有较强的相关性。同时,使用假设检验可以判断是否发生电信诈骗的案例中,这两个指标的相关性是否显著。
根据附件中的数据,我们可以得到如下结果:
详细请查看: