【十大排序算法】桶排序

news2024/12/24 0:21:09

在时间的琴弦上，桶排序如同一曲清澈的溪流，将数字的芬芳温柔地分拣，沉静地落入各自的花瓣般的容器中。

文章目录

一、桶排序
二、发展历史
三、处理流程
四、算法实现
五、算法特性
六、小结
推荐阅读

一、桶排序

桶排序（Bucket sort）是一种排序算法，其工作原理是将数组分到有限数量的桶里。每个桶再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序），最后依次把各个桶中的记录列出来得到有序序列。

桶排序的核心在于合理设计桶的数量和每个桶的范围，使得数据能均匀分布到各个桶中，进而降低后续排序的复杂度。当待排序数据分布均匀且范围已知时，桶排序能充分利用数据特性，实现高效排序。

二、发展历史

桶排序是一种排序算法，其发展历史可以追溯到 1970 年代。以下是桶排序的发展历史：

早期思想： 桶排序最早可能出现在计算机科学的早期阶段，但并没有被正式提出。早期的计算机科学家可能会考虑将数据分组放入“桶”中，然后对每个桶中的数据进行排序。
1970 年代： 桶排序的概念可能最早出现在 1970 年代。在这个时期，人们开始思考如何改进传统的比较排序算法，以提高排序的效率。桶排序被提出作为一种可能的改进方法。
1980 年代： 在这个时期，桶排序算法开始被正式提出和研究。人们开始探讨如何实现桶排序以及如何优化它的性能。1980 年代是计算机科学发展的重要时期，许多经典的算法被提出和研究。
1990 年代： 随着计算机硬件的发展和算法研究的深入，桶排序算法得到了更广泛的应用和研究。人们开始研究如何在不同情况下使用桶排序，并探索如何优化算法以提高排序的效率。
2000 年代至今： 桶排序算法在这个时期得到了进一步的发展和改进。随着大数据时代的到来，人们开始思考如何将桶排序算法与并行计算、分布式计算等技术相结合，以应对更大规模的数据排序问题。

三、处理流程

场景假设：我们需要将下面的无序序列使用桶排序按从小到大进行排序。
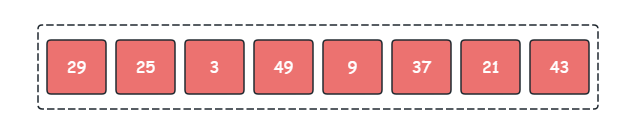
workspace (15).png
桶排序的流程如下：

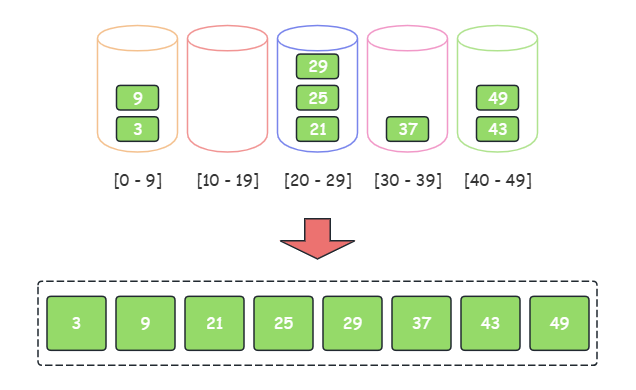
初始化桶：首先，我们需要确定桶的数量。在这个例子中，我们可以选择 10 个桶，每个桶代表一个范围，例如，第一个桶存储 0-9 之间的数，第二个桶存储 10-19 之间的数，以此类推。

workspace (17).png

分配元素到桶：然后，我们将每个元素放入对应的桶中。例如，29 会被放入第三个桶 [20-29]，3 会被放入第一个桶（0-9），依此类推。

workspace (20).png

对每个桶进行排序：接下来，我们对每个桶中的元素进行排序。我们可以使用任何排序算法，例如插入排序、选择排序等。

workspace (21).png

合并桶：最后，我们按照桶的顺序，依次取出每个桶中的元素，合并成一个有序序列。

workspace (22).png

四、算法实现

public class BucketSort {
    public static void bucketSort(int[] arr) {
        // 检查数组是否为空或者长度为0
        if (arr == null || arr.length == 0) {
            return;
        }

        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;
        // 找出数组中的最大值和最小值
        for (int num : arr) {
            max = Math.max(max, num);
            min = Math.min(min, num);
        }

        // 计算桶的数量
        int bucketNum = (max - min) / arr.length + 1;
        ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
        for (int i = 0; i < bucketNum; i++) {
            bucketArr.add(new ArrayList<>());
        }

        // 将每个元素放入桶
        for (int i = 0; i < arr.length; i++) {
            int num = (arr[i] - min) / (arr.length);
            bucketArr.get(num).add(arr[i]);
        }

        // 对每个桶进行排序
        for (int i = 0; i < bucketArr.size(); i++) {
            Collections.sort(bucketArr.get(i));
        }

        // 将桶中的元素赋值到原序列
        int index = 0;
        for (ArrayList<Integer> arrayList : bucketArr) {
            for (Integer integer : arrayList) {
                arr[index++] = integer;
            }
        }
    }
}

算法时间复杂度分析：

情况	时间复杂度	计算公式	公式解释
最好情况	$O (n + k)$	$T (n) = n + k$	当输入的数据可以均匀的分配到每一个桶中，每个桶中的数据量很小，可以看作是常数时间，所以此时的时间复杂度为 $O (n + k)$ 。这里的 $n$ 是待排序元素的数量， $k$ 是桶的数量。
平均情况	$O (n + k)$	$T (n) = n + k$	在平均情况下，每一个桶中的数据将近为 $n / k$ ，那么排序的时间复杂度近似于 $O (n + k)$ 。这里的 $n$ 是待排序元素的数量， $k$ 是桶的数量。
最坏情况	$O(n ^ 2)$	$T(n) = n ^ 2$	当所有的数据都分配到一个桶中时，此时就退化为了基数排序，所以最坏时间复杂度为 $O(n ^ 2)$ 。这里的 $n$ 是待排序元素的数量。

五、算法特性

桶排序是一种分布式排序算法，其特性包括：

稳定性： 如果在桶内排序时使用的是稳定的排序算法（比如插入排序），并且在合并桶的过程中保持桶的顺序，则桶排序是稳定的。稳定性指的是相等元素的相对位置在排序前后不发生改变，桶排序在满足上述条件时能够保持相等元素的相对顺序。
原地性： 桶排序通常不是原地排序算法，因为它需要额外的空间来存储桶以及桶内的元素。桶排序的空间复杂度与输入数据的特性和桶的数量有关，通常情况下需要额外的线性空间。
适用场景： 桶排序适用于输入数据分布较均匀的情况，特别是适用于有着已知范围的整数排序。在这种情况下，可以根据范围划分桶，每个桶内的数据量相对较小，利于高效地进行排序。
分桶思想： 桶排序将待排序的元素分配到不同的桶中，每个桶内的元素具有一定的范围，通常是根据输入数据的特性和分布情况确定的。分桶的过程可以利用映射函数，将元素映射到对应的桶中。
桶内排序： 桶排序对每个桶内的元素进行排序，可以使用其他排序算法，如插入排序、快速排序等。桶内排序通常选择适合当前桶大小的高效排序算法。
桶间排序： 当所有的桶都排好序后，桶排序将按照桶的顺序依次合并起来，形成最终的有序序列。通常情况下，可以简单地按照桶的顺序将各个桶中的元素依次输出，从而形成有序序列。