Logistic回归分析用于研究X对Y的影响,并且要求Y必须为分类数据,并且根据Y的分类不同,需要选用不同的模型。
如果Y为二分类,如患病和不患病,那么普通的二元logistic回归就可以解决问题;
如果Y为有序多分类,如病情的轻、中、重度,那么二元logistic就不适用了,需要等级Logistic回归登场!
但是SPSS进行等级logistic回归,不仅要进行哑变量设置转换,还不能批量进行单因素分析,最终结果呈现还没有直接给定OR值,需要手工计算OR值,十分麻烦!R语言可以解决这些问题,但需要一定的代码基础,对统计小白十分不友好!
因此,这里推荐大家使用浙江中医药大学郑卫军教授基于R语言开发的统计分析平台——风暴统计!
结果输出简洁,直接生成三线表,支持word版下载!
平台是基于R语言进行开发,结果准确性有保障!
全部菜单式操作,统计小白也可以轻松上手!
下面我们就通过一份实操数据,给大家详细介绍一下风暴统计平台快速合并单因素与多因素分析结果的实操流程!
logistic回归具体网址:https://shiny.medsta.cn/log/
或者百度、必应Bing搜索“风暴统计”
本平台上线的所有工具都是免费的

1.进入风暴统计平台
首先,进入风暴统计平台,依次点击"风暴智能统计"—"logistic回归分析"—"logistic回归"!
这里我们不再赘述数据的导入与整理过程,详细教程大家可以点击下方链接:
详细指南!风暴统计如何高效导入数据,统计分析快人一步?
详细版!如何利用风暴统计进行数据的整理转换?
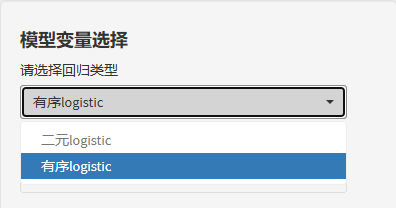
等级/有序Logistic回归就和之前的二元logistic回归在同一个模块,回归类型直接选择"有序logistic"就好!
第1步:logistic回归变量选择
首先,选入变量,包括因变量、自变量、自变量。
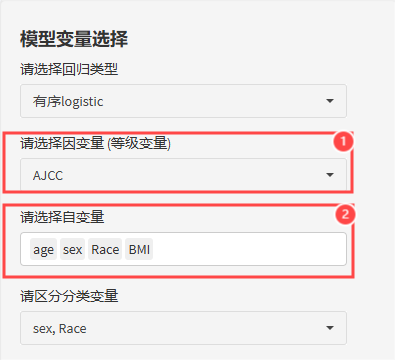
①因变量
这里因变量必须是≥3分类的等级变量,建议以数字形式进行赋值。
②自变量
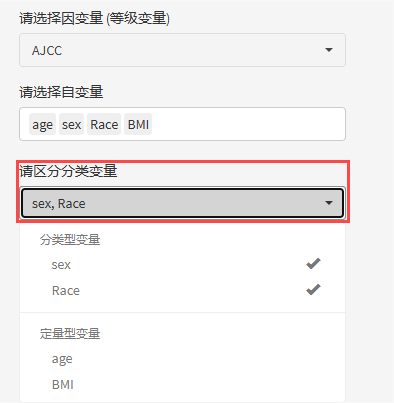
自变量不限制定量或分类,全部选入后,平台会自动将分类数<5类的变量归为分类变量。
如果需要变量以分类形式进入模型,在此处勾选特定变量即可;
如果变量分类数<5,但是希望以定量形式进入模型,也可以取消勾选。
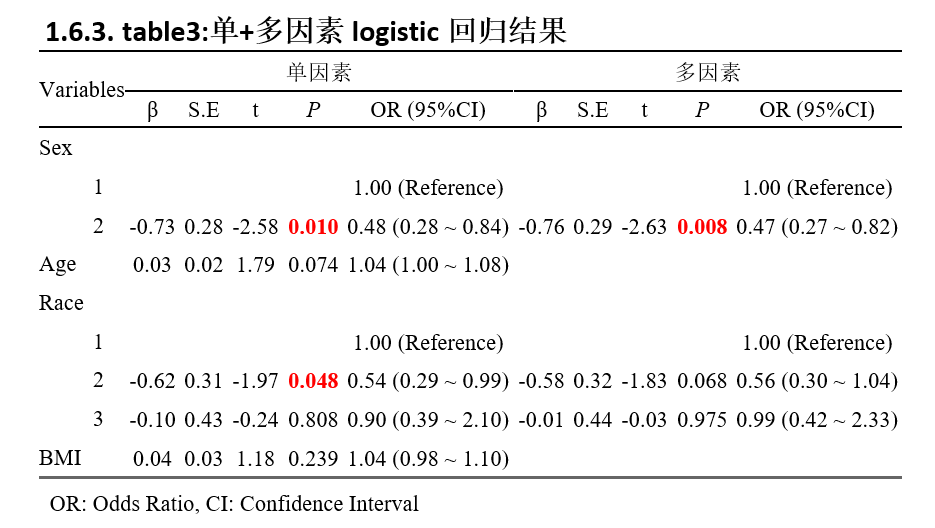
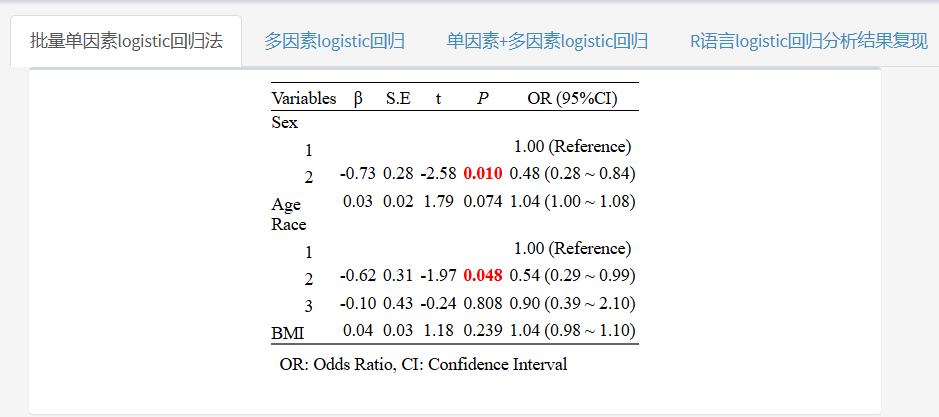
完成选择后,右侧就会实时给出单因素等级logistic回归结果了!
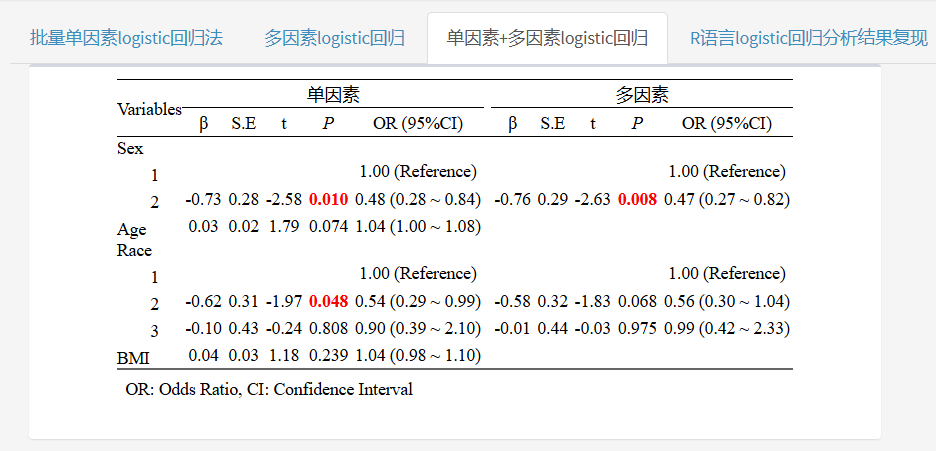
第2步:多因素回归设置
接着进行多因素回归,P阈值及回归方式的选择。
P阈值自行选择,如果自变量个数过少,可以适当放宽标准,0.1、0.2也都是可以的。当选择不限制时,选入的全部自变量都将纳入多因素回归分析。
回归方法,平台也提供了多种选择:双向逐步回归,向前逐步回归,向后逐步回归以及考虑到有时P值大于0.05的变量在逐步回归时也会留在模型中,新增了根据P<0.05的原则开展逐步回归!

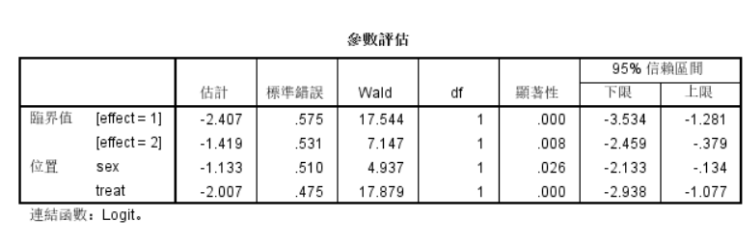
完成后,右侧直接生成规范的三线表结果!单因素与多因素结果直接合并在一张三线表格中!
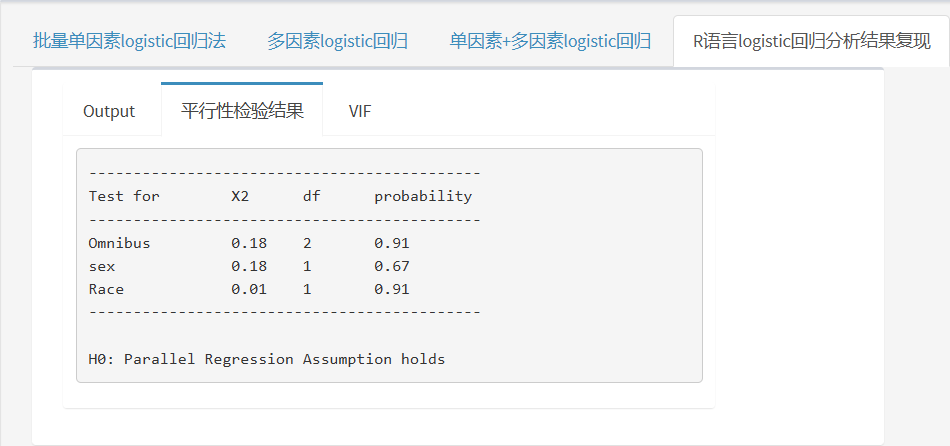
此外,平台还给出了平行性检验结果,即检验自变量各取值水平对因变量的影响在各个回归方程中是否相同。平行性是有序Logistic回归的前提条件,一般认为检验P>0.05则符合有序logistic回归的适用条件,否则,建议更换模型分析!
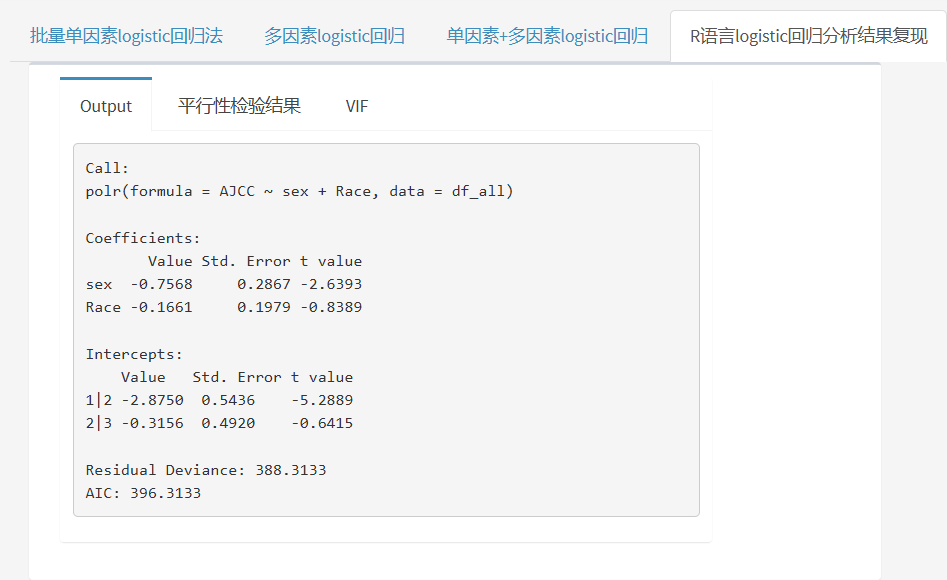
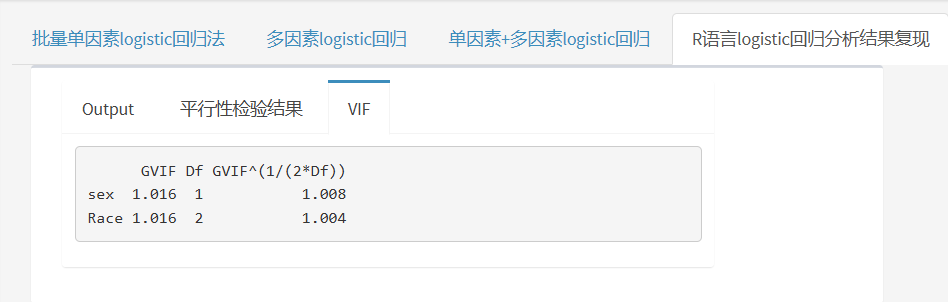
此外,还有R语言的原始输出结果及方差膨胀因子(检验变量间共线性)以供参考!
4.下载结果
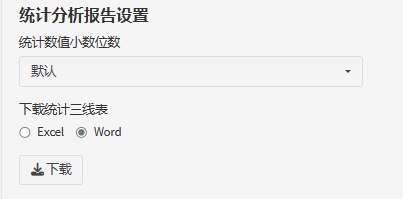
完成分析后,可以选择小数位数,默认情况下,P值为3位小数,其他统计量为2位小数。
指定小数位数后,P值与统计量的小数位数将会统一。调整完成后,下载最终的三线表结果,平台支持下载excel或word!
下载得到的word版单因素与多因素合并结果也十分的简洁美观!三线表及下标脚注,全部一步到位!
|
如果您在风暴统计平台的使用过程中有任何的建议或疑问,欢迎加入我们的讨论群!群里郑老师与助教会在群内解答!

统计机器人交流群