在SwiftUI中,Shape协议允许开发者定义可重用的图形,这些图形可以用于绘制界面元素,如按钮、背景、边框等。通过实现 Shape 协议,可以创建完全自定义的图形,并控制其绘制方式。本文将详细介绍如何在 SwiftUI 中创建自定义 Shape,并提供几个示例。
Shape 协议基础
在SwiftUI中,Shape是一个协议,要实现它,需要实现一个方法path(in rect: CGRect) -> Path。这个方法返回一个 Path 对象,该对象定义了图形的具体绘制路径。
绘制直线
绘制直线还是比较简单的,比如下面的代码,绘制了一个三角形。
struct Triangle: Shape {
func path(in rect: CGRect) -> Path {
Path { path in
path.move(to: CGPoint(x: rect.midX, y: rect.minY))
path.addLine(to: CGPoint(x: rect.maxX, y: rect.maxY))
path.addLine(to: CGPoint(x: rect.minX, y: rect.maxY))
path.closeSubpath()
}
}
}
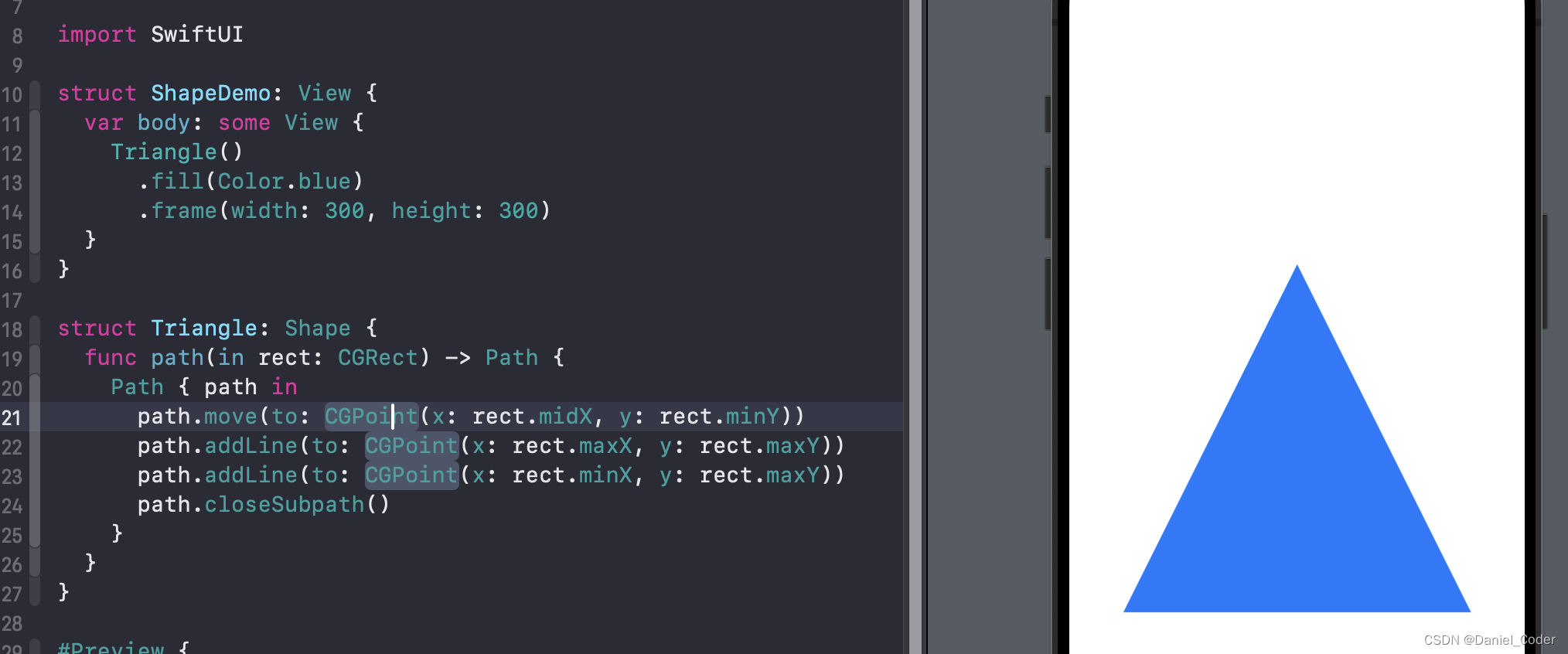
在绘制开始时,先调用move方法定位起始点,然后通过addLine方法,并传入下一点的信息,绘制直线,最后闭合整个绘制路径即可。
下面绘制一个复杂点的,五角星。
struct StarShape: Shape {
func path(in rect: CGRect) -> Path {
let h = Double(min(rect.size.width, rect.size.height)) // 确保星形保持正方形区域内
let c = CGPoint(x: rect.size.width / 2, y: rect.size.height / 2) // 中心点
let r = h / 2.0 // 外圈半径
let angle = Double.pi * 2 / 5 // 每个星角的角度
var path = Path()
// 计算五个外圈顶点
let points: [CGPoint] = (0..<5).map { i in
let adjustedAngle = angle * Double(i) - Double.pi / 2
return CGPoint(x: c.x + r * cos(adjustedAngle), y: c.y + r * sin(adjustedAngle))
}
// 计算五个内圈顶点
let r2 = r * sin(angle / 2) / (1 + sin(angle / 2)) // 内圈半径
var innerPoints: [CGPoint] = []
for i in 0..<5 {
let adjustedAngle = angle * Double(i) - Double.pi / 2 + angle / 2
let point = CGPoint(x: c.x + r2 * cos(adjustedAngle), y: c.y + r2 * sin(adjustedAngle))
innerPoints.append(point)
}
// 绘制星形
path.move(to: points[0])
for i in 0..<5 {
path.addLine(to: innerPoints[i])
path.addLine(to: points[(i + 1) % 5])
}
path.closeSubpath()
return path
}
}
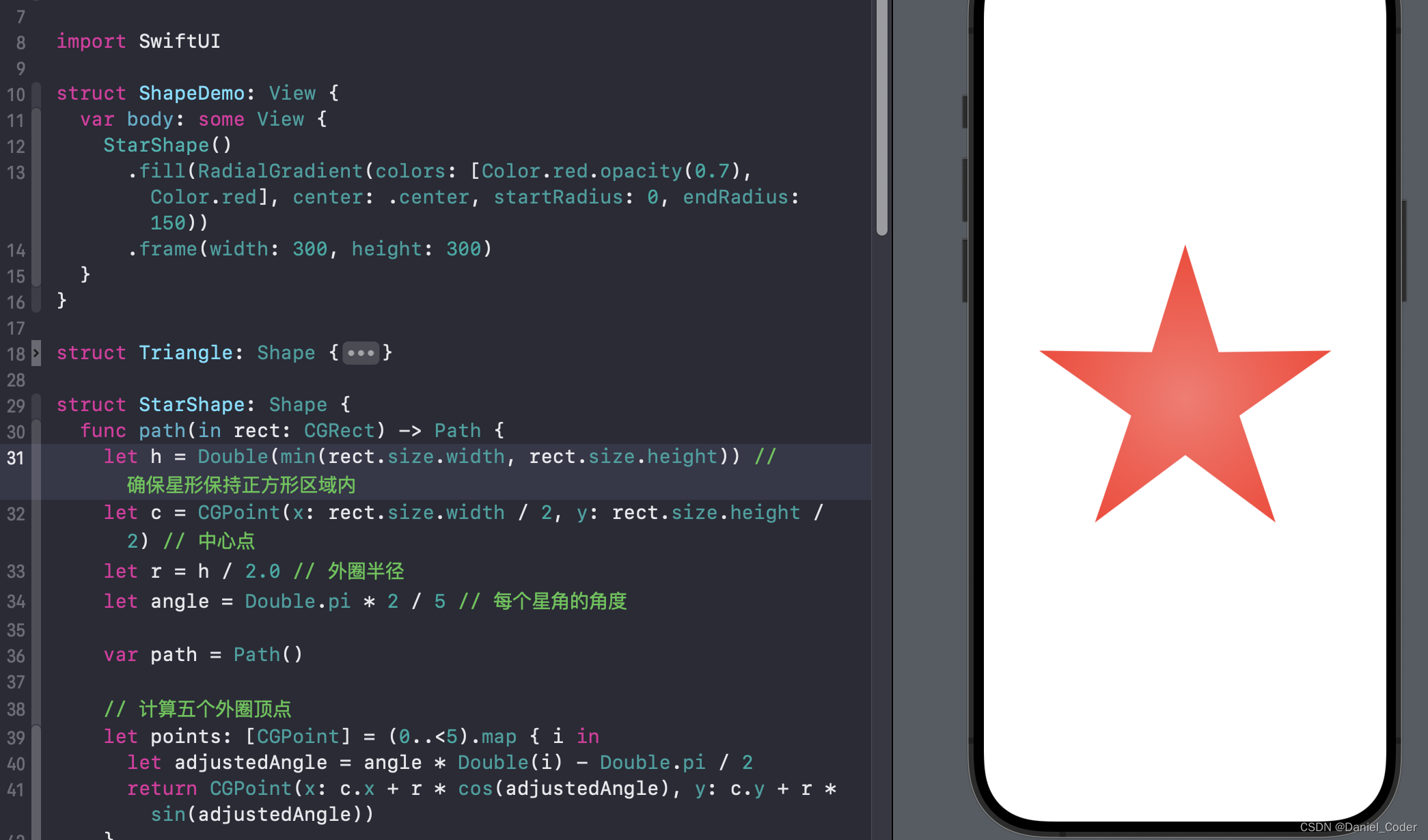
绘制圆弧
圆弧可以通过 Path 的 addArc 方法来绘制。这个方法需要几个参数:圆心(center)、半径(radius)、起始角度(startAngle)、结束角度(endAngle)以及是否顺时针(clockwise)。
上面的参数都比较好理解,角度是从圆的正东方向开始测量的。这里特别说一个clockwise是否顺时针参数。
clockwise参数决定了创建圆弧的方向,最终路径的实际方向取决于转换参数和绘制路径的上下文的当前转换。然而,因为SwiftUI默认使用一个垂直翻转的坐标系(原点在视图的左上角),指定一个顺时针的弧线在应用转换后会导致一个逆时针的弧线。
比如下面的示例,clockwise为false,逆时针绘制,而弧线是从右侧画到左侧的,顺时针绘制的,如果将沿着X轴将Y轴上下翻转,再看就是逆时针绘制了,这也和我们传的参数值对上了。
struct ArcShape: Shape {
func path(in rect: CGRect) -> Path {
var path = Path()
path.addArc(center: CGPoint(x: rect.midX, y: rect.midY),
radius: rect.width / 2,
startAngle: .degrees(0),
endAngle: .degrees(180),
clockwise: false)
return path
}
}

绘制贝塞尔曲线
二次贝塞尔曲线
在 SwiftUI 中,Path类提供了addQuadCurve(to:control:) 方法,这是用于绘制二次贝塞尔曲线的工具。二次贝塞尔曲线是一种使用单个控制点来定义曲线形状的方法,它可以创建平滑的曲线,常用于图形设计和动画中。
addQuadCurve(to:control:) 方法接受两个参数:
to: CGPoint 类型,表示曲线的终点。
control: CGPoint 类型,表示控制点,这个点决定了曲线的弯曲程度和方向。
二次贝塞尔曲线基于线性插值。给定一个起点(当前路径的最后一个点),一个终点(to 参数),和一个控制点(control 参数),曲线在起点和终点之间插值,控制点则决定曲线的弯曲程度和方向。
struct QuadCurveShape: Shape {
func path(in rect: CGRect) -> Path {
var path = Path()
// 设置起点
path.move(to: CGPoint(x: rect.minX, y: rect.midY))
// 添加二次贝塞尔曲线
path.addQuadCurve(to: CGPoint(x: rect.maxX, y: rect.midY),
control: CGPoint(x: rect.midX, y: rect.minY))
return path
}
}
我们首先使用 move(to:) 方法设置曲线的起点。
然后,使用 addQuadCurve(to:control:) 方法添加一条二次贝塞尔曲线。曲线的终点设置在矩形的最右侧中点,控制点设置在矩形的顶部中点。这样,曲线从左侧中点开始,向上弯曲到顶部中点,然后再向下弯曲到右侧中点。

三次贝塞尔曲线
Path 类提供了 addCurve(to:control1:control2:) 方法,用于绘制三次贝塞尔曲线。三次贝塞尔曲线比二次贝塞尔曲线提供更高的控制精度,因为它使用两个控制点而不是一个,允许创建更复杂的曲线形状。
addCurve(to:control1:control2:) 方法接受三个参数:
to: CGPoint 类型,表示曲线的终点。
control1: CGPoint 类型,表示第一个控制点,这个点主要影响曲线的起始部分。
control2: CGPoint 类型,表示第二个控制点,这个点主要影响曲线的结束部分。
三次贝塞尔曲线通过两个控制点来定义曲线的形状。起点和终点(to 参数)定义了曲线的起始和结束位置,而两个控制点(control1 和 control2)则共同决定了曲线的整体弯曲路径。
struct CurveShape: Shape {
func path(in rect: CGRect) -> Path {
var path = Path()
path.move(to: CGPoint(x: rect.minX, y: rect.midY))
path.addCurve(to: CGPoint(x: rect.maxX, y: rect.midY),
control1: CGPoint(x: rect.minX + rect.width / 3, y: rect.minY),
control2: CGPoint(x: rect.maxX - rect.width / 3, y: rect.maxY))
return path
}
}
我们首先使用 move(to:) 方法设置曲线的起点。
然后,使用 addCurve(to:control1:control2:) 方法添加一条三次贝塞尔曲线。曲线的终点设置在矩形的最右侧中点,第一个控制点设置在矩形的左侧三分之一处的顶部,第二个控制点设置在矩形的右侧三分之一处的底部。这样,曲线从左侧中点开始,先向上弯曲到第一个控制点,然后向下弯曲到第二个控制点,最后平滑过渡到右侧中点。

下面这个图是关于二次和三次贝塞尔曲线的示意图:
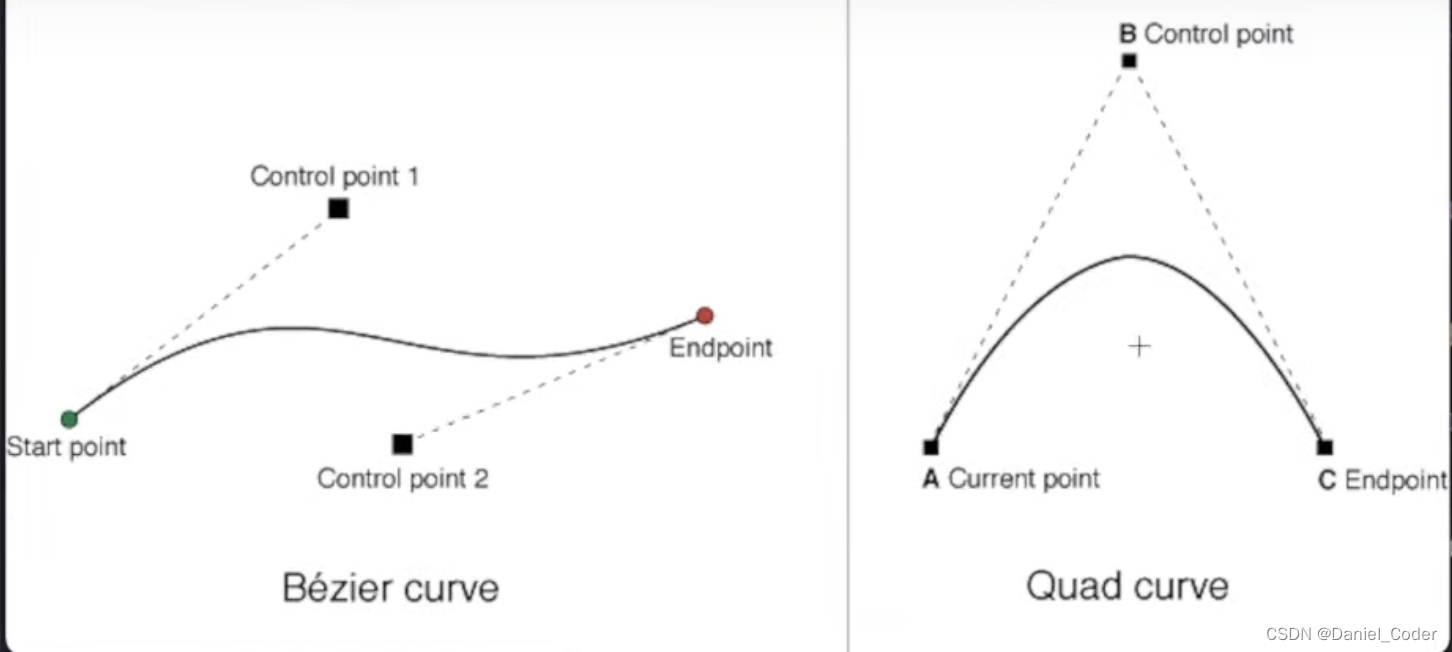
写在最后
本文主要介绍了常用的一些自定义图形,绘制直线,弧线,以及曲线,感兴趣的朋友还可以将这些组合起来使用,绘制符合App设计的图形。
最后,希望能够帮助到有需要的朋友,如果觉得有帮助,还望点个赞,添加个关注,笔者也会不断地努力,写出更多更好用的文章。