前言:
写在这里,这是我小论文的方向,但是以前从来没有接触过微电网及优化调度算法,所以呢,开始展开积极自救。两个月前,我开始重拾Matlab编程以及最简单的微电网知识,以及看一些论文,逐渐接触了gurobi求解器,混合整数线性规划算法等,最近一段时间,在学习粒子群优化算法,看视频学习的方式,总归是缺了点东西,即------我想知道的,视频里可能没有讲到。所以我感觉适合自己的方式就是“视频学习快速了解+阅读论文+解析代码+人工智能软件去提问”,这样的搭配让我觉得非常舒服,所以,在这里和大家分享一下,希望大家也找到自己的学习方法。重点知识我会用红色或者加粗进行标注,方便大家跳跃式观看。在观看下面的这些文字时,希望你一定在评论区先找到我留下的代码文件链接,在自己的电脑上运行一下,粗略看一看各个部分函数的组成及功能,然后再来看我的一个详细总结归纳。
本文的目标:
让新手小白知道粒子群算法的运行逻辑,能够知道每一步是在做什么,如果换一个应用环境,可以根据这个编程的逻辑思路使用粒子群算法去优化-----------------分析粒子群算法的编程思路。
基础知识:
粒子群算法的原理,很多前辈已经讲解过,大家可以在各种平台上就行搜索观看学习。
1.非支配解:非支配解是多目标优化中的一个重要概念。在多目标优化问题中,通常会同时考虑多个相互冲突的目标函数,寻找一个单一的最佳解是不可能的,因为改善其中一个目标通常会牺牲其他目标的表现。因此,我们转而寻找所谓的“帕累托最优”解集,其中的每一个解都不是其他解的严格改进。举个例子:
假设我们正在为家庭选购一款沙发,现在有三个选项A、B、C,它们的性能指标如下:
- 方案A:美观度评分为9(满分为10分),价格为$1200。
- 方案B:美观度评分为8,价格为$1000。
- 方案C:美观度评分为7,价格为$800。
在这个家具选购的场景中,我们可以分析各方案的非支配关系:
- 方案A与B相比,A在美观度上胜出,但价格更高。这意味着A不能在所有方面都优于B,即A不能支配B。
- 方案B与C相比,B在美观度上更高,但价格也略高。因此,B也不能在所有目标上都优于C,即B不能支配C。
- 方案C与A相比,C的价格更为亲民,但在美观度上不及A。这表明C也不能支配A。
由于没有一个方案能在美观度和价格这两个目标上同时超越其他所有方案,因此这三个沙发方案选项各自都是非支配解,构成了一个美观度与价格的帕累托前沿。在这个前沿上,每个点(沙发选项)代表了美观度与价格的不同权衡。消费者可以根据自己对美观度和预算的重视程度,从这个帕累托前沿中选择最满意的沙发。例如,如果追求极致美观不在乎价格,可能会倾向选择A;若预算有限但希望性价比高,则C可能更合适。--------------这也就涉及到为什么要建立一个数据的仓库,用于存储具有高质量的解,在这个例子中就是,存储方案A,B,C,以供用户选择,无论是你有何种需求,性价比,美观度,价格实惠,都可以在这个仓库中找到对应的最优解。
2.可行解:如果一个解,能够满足所有的约束条件,那么它就被称作可行解。非支配解一定是可行解吗?在微电网的论文模型中,非支配解是可行解之一。
3.非占优解:就是非支配解的等价描述。
4.粒子群算法中可行解的维度是什么意思?
可行解的维度就是,单个粒子,在搜索空间中,所具有变量的数量。
比如可行解的数量=1,则该粒子仅仅只有一个变量,在以为空间中进行搜索,如果可行解的数量=3,则该粒子有3个变量,在三维空间中搜索最优(可以在大脑中想象一下)。
5.种群数量与迭代次数:比如种群数量为20,迭代次数为50,那么在初始化时,会生成20个初始粒子,然后进行一次迭代(这20个粒子的方向,速度等都会进行改变,并记录个体最优和全局最优),就视作进行了一次探索。这样这20个粒子需要进行50次迭代。
编程思路:(颜色一致为同一层,依次为红,深蓝,紫)
1.导入微电网仿真模型所需的风力发电数据,光伏发电数据,负荷数据,24小时的电价数据。
2.设置微电网、粒子群算法的全局变量,并进行赋值操作。
3.调用粒子群算法函数mopso,并且将函数的返回值,赋值给变量mm。
(1)在函数mopso中,设置本函数所需要的变量并赋值。(即各个部件出力上下限)
(2)设定种群规模,比如粒子数量,权重参数,维度网格数,通货膨胀率,数据上下限等。
(设定数据上下限是为了保证粒子不会飞出可行解的区域,典型例子群算法-->变异率设置为0)
(3)调用Partical()函数生成一组合格的初始化粒子,如果不合格就在迭代允许范围内,不断重复生成,直至合格,才继续生成下一个粒子。(举个例子,如果粒子种群规模为100个,则需要生成100个粒子,如果第20个粒子它不是可行解即不合格,那么可以循环迭代200次,直至生成一个合格的粒子才停止,然后继续生成第21个粒子;初始化一组粒子的过程,可以理解为在一个围棋特定的约束范围内撒一把棋子,然后棋子的行列位置,即一个2维的解(粒子),如果棋子的位置不在特定约束范围内,那么重新抛,直至出现在特定棋盘区域,或者,耗尽200次机会)
a.在函数Partical内定义结构体的属性,比如粒子的位置向量,解空间的上限向量,下限向量,粒子的速度向量,目标函数值向量(因为是多目标,所以将单个目标函数的值放在一个数组内),个体最优解,不可行解,支配解等。
b.编写功能函数,生成粒子、得到粒子下一位置、得到粒子速度、得到粒子个体历史最优等
c.在生成粒子和粒子进化函数中,使用problem句柄,调用特定的计算公式函数,计算该粒子(这一组特定变量值)对应的经济成本,环境成本。
(4)创建一个存档仓库,用于记录高质量的解(即非支配解,并在每一个种群进化后更新它)
(5)这100个粒子,进行100次迭代,每一次迭代后,都是在各个粒子在考虑上一次的位置,个体最优,全局最优,自身惯性之后进行的位置调整,所以会逐渐趋近于全局最优解,迭代的次数为10次的质量,从概率上讲,获得全局最优解的可能性远远小于200次迭代得到的解的质量。
a.创建一个函数,需要循环100次(上面说了需要进行100次迭代)
b.从第一轮至100轮,每一次循环都需要通过公式更新每个粒子的方向,加速度,惯性(所以是双重for循环)
c.在每一轮中,都将本轮的粒子最优进行筛选,放入存档仓库中。
(6)通过画图函数,展示这100次的动态迭代的结果。
4.通过结构体的属性,得到迭代100次之后的非支配解的数量mm
5.通过for循环,计算mm个非支配解他们各自对应的总目标数值(目标函数1值+目标函数2值),这个总目标数值肯定是mm个。
6.寻找这mm个元素中的最小值以及对应索引的位置。
7.根据索引位置,找到这一个数组(144个元素),并按照24小时,进行逐个拆分(一天24小时,如风力发电机,只能产生24个元素的数据,144/24=6,即这个微电网的数据由6个部分组成)
8.将拆分的小段数组,通过画图展示(比如在总目标最小的条件下,风力发电机24小时消纳情况,光伏消纳情况,柴油机出力情况,从主网购售电情况)。
这个就是大致的一个编程思路。
代码运行
当一个代码开始运行之后,如何确定我们理解的思路,我们需要查看的变量,在什么位置呢?即如何通过Matlab软件来找到代码求解出的结果呢?我们来关注一下

在主程序中,我们可以看见,多目标粒子群封装函数mopso,它有一组返回值,传递给了变量mm。也就是这个mm中,有粒子群算法的所有返回信息。

打开这个mopso函数,我们可以看见,这几行中,设定了一个数组的不同位置的上下限范围,是实际上就是这6种机组24小时出力的各自对应上下限,为了初始化的解一定要在这个范围内,偏离这个范围,就是不可行解。

在mm中,发现有如下几个变量,最重要的是这个swarm,mm.swarm存储的是粒子群迭代100次之后的非支配解,也就是高质量解,无论以单独的经济效益,或者环境效益,或者用户效益,其最优解只可能从这一组(这72个非支配解)中得到。
 上图中1,和2处,他们是同一个存档库(仓库),不过一个是打印在对话窗口,一个是直接查看的变量的元素大小。继续点击上图2处,就会看到下图的结果。上图2中表示记录了72个非支配解(粒子即一组解),下图中就是这72个解在仓库中的排序。
上图中1,和2处,他们是同一个存档库(仓库),不过一个是打印在对话窗口,一个是直接查看的变量的元素大小。继续点击上图2处,就会看到下图的结果。上图2中表示记录了72个非支配解(粒子即一组解),下图中就是这72个解在仓库中的排序。

我们需要找到在“运行成本”+“经济效益”下的总目标最小的函数,因此需要先把72个挨个计算一下各自对应的总目标函数,然后找到最小的那个总目标函数所对应的粒子,取出其位置索引,将这个粒子(一组变量的解)放在图形界面进行展示。
-------------------------------------------跳回主程序代码处--------------------------------------

从第59行代码至61行代码,可以看出来是在进行求解各个粒子的总目标函数数值,并赋值给object数组,然后第62行代码,在object数组中寻找最小的总目标函数值,将其位置索引取出给变量p。第63行代码,mm.swarm(1,p)就是对应的总目标函数值最小的粒子。是不是有点熟悉,这个mm.swarm,他就是上面图中查看的存储72个非支配解(高质量粒子)的仓库。
-------------------------------------------继续查看变量-----------------------------------------------

根据刚才代码我们可以知道,变量p代表位置总目标函数值最小的粒子的位置,pg就是这个粒子(回顾第62,63行代码)。话不多说,我们通过mm.swarm的第36个元素,去查看一下内部的解是否和图形表示的一样。


这里的这个X就是我们要找的粒子的变量的数值。其中,x表示粒子的空间中的坐标,这个粒子的解是一个double型数组,而且该数组由144个元素(144个变量的144个解构成)。继续点击查看x,看到了分别对应,光伏24小时,风力发电机24小时等的最佳出力数据(最优粒子肯定是对应的最优解,这个解不同于最开始代码从外部导入的数据,那个数据是预计的发电数据,这个变量里才是,在总体目标最优情况下,最应该给的数据,实际上应该出力的数据。),举个粒子,你一个小时之后要去跑步了,你妈妈给你准备了一大桌子菜,让你多吃点,吃饱了才有力气跑步,但是你知道,吃太多了跑步对胃不好,所以你为了保持整体机能的最优状态,于是喝了两口稀饭,吃了一点蛋白质,又管不住嘴馋,吃了一口可乐鸡翅和一块红烧肉。我们可以理解为这就是身体机能最优时候的进餐方案解,其余你妈妈做的一桌子菜品可能都吃不了。这一桌子菜品,就相当于Matlab程序导入的那个excel中的预计出力数据。

在这里,我们可以看见,位置0~24是光伏最佳出力数据(我们最初设置的排序,还记得吗?)其中8~17点,光伏出力数据如下。
我们对应看一下光伏24小时出力图形展示:
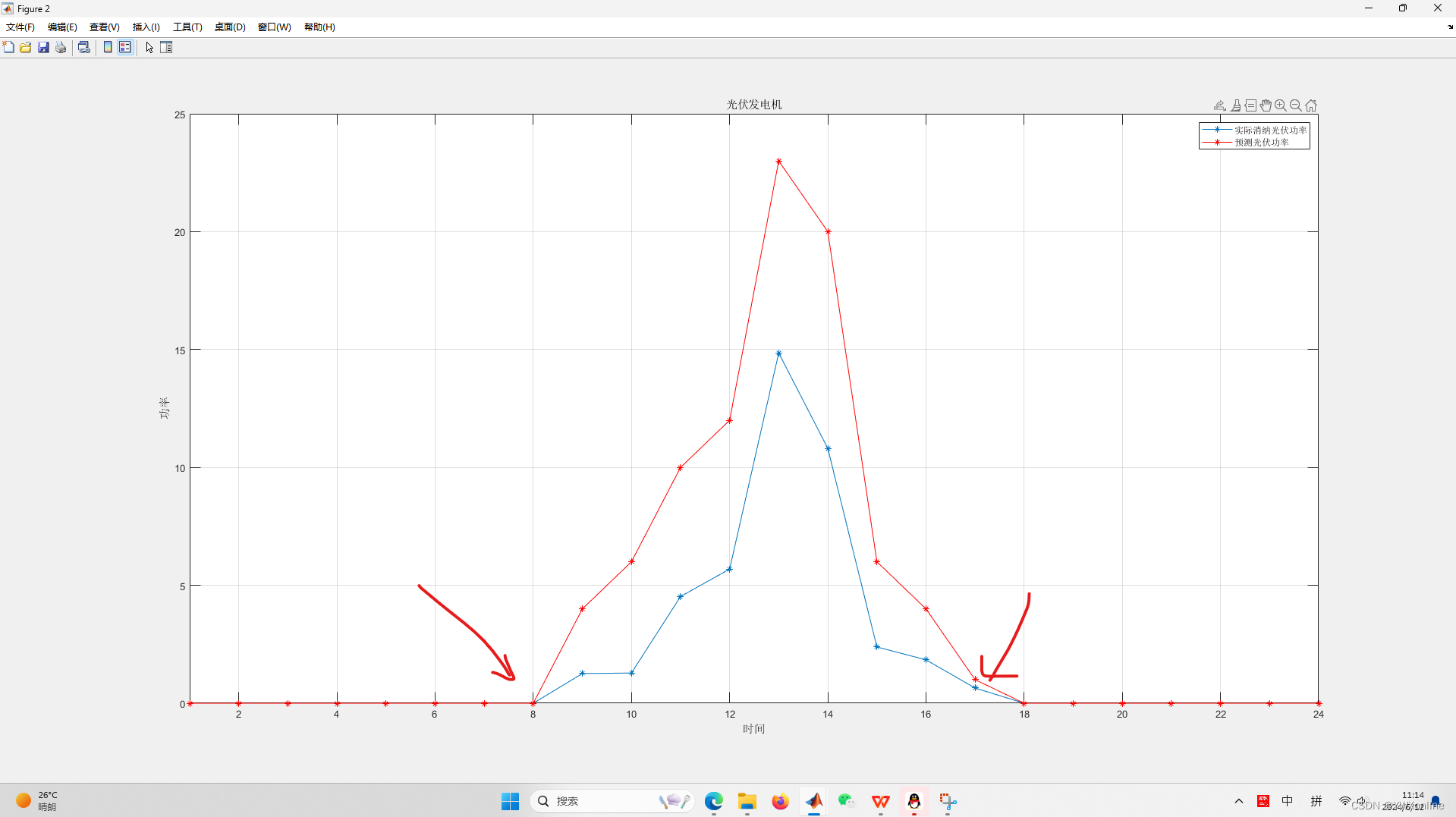
确实,上面这个图形和上上个图形8~17时的数据时完全吻合的,而且将最开始的excel中的数据进行了绘制,蓝色才是最佳出力(微电网在总目标函数值最小情况下,能够消纳的光伏电量)。
依次类推,可以看到其余的各个部分出力,这里我就不再赘述,可以自己下载代码看一下。
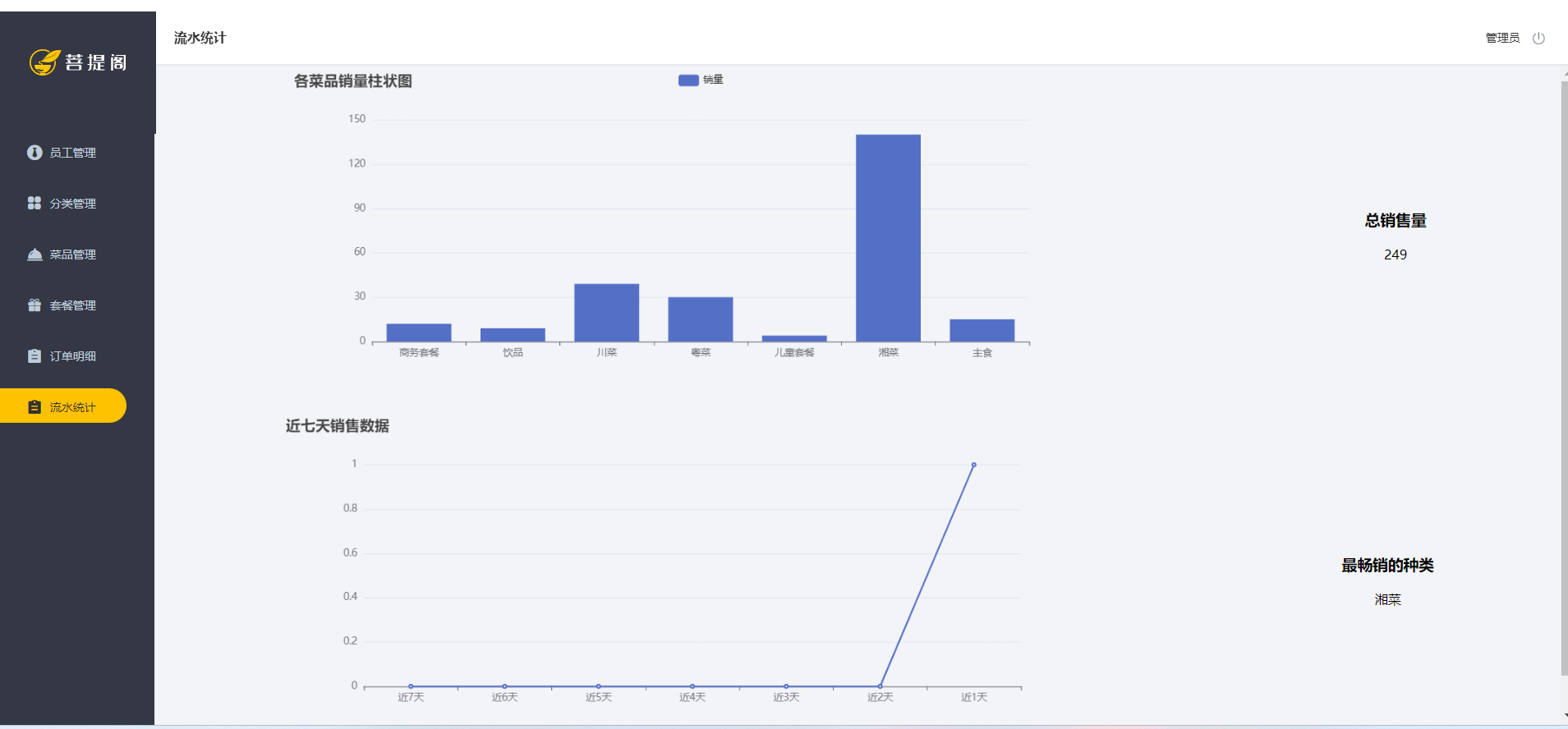
代码的运行总结果如下:
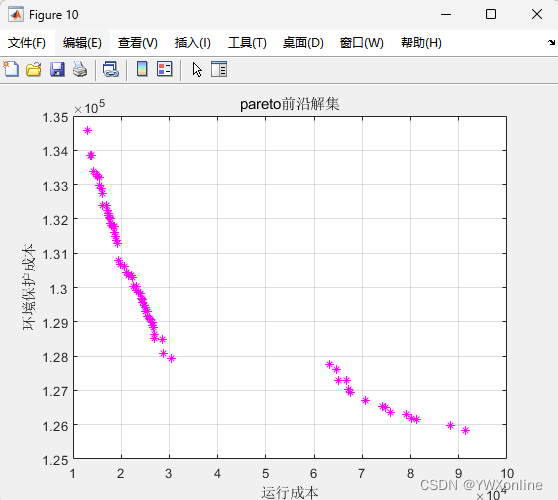
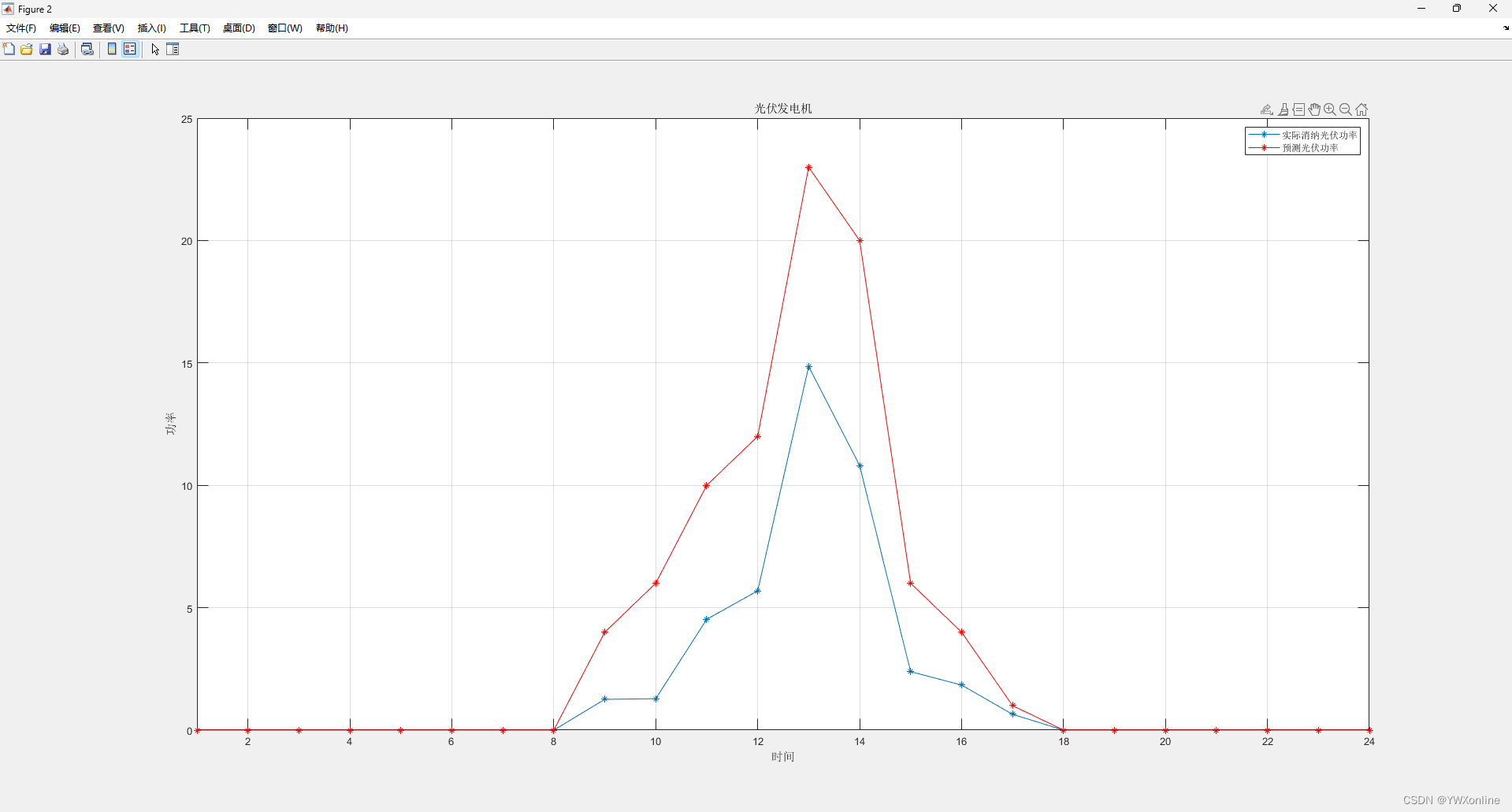


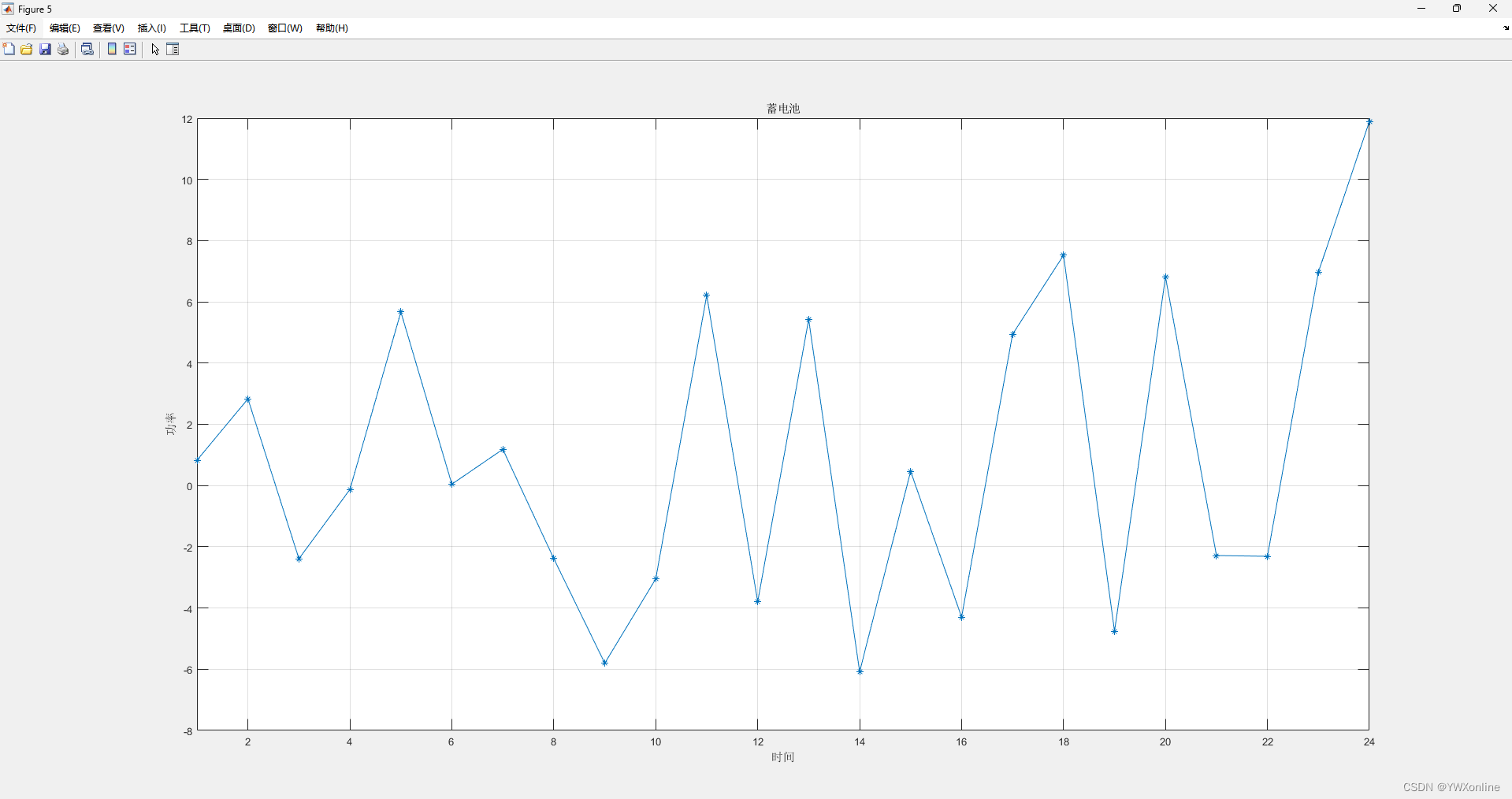

微电网的负荷是固定的,所以不需要求解,只需要作图即可。

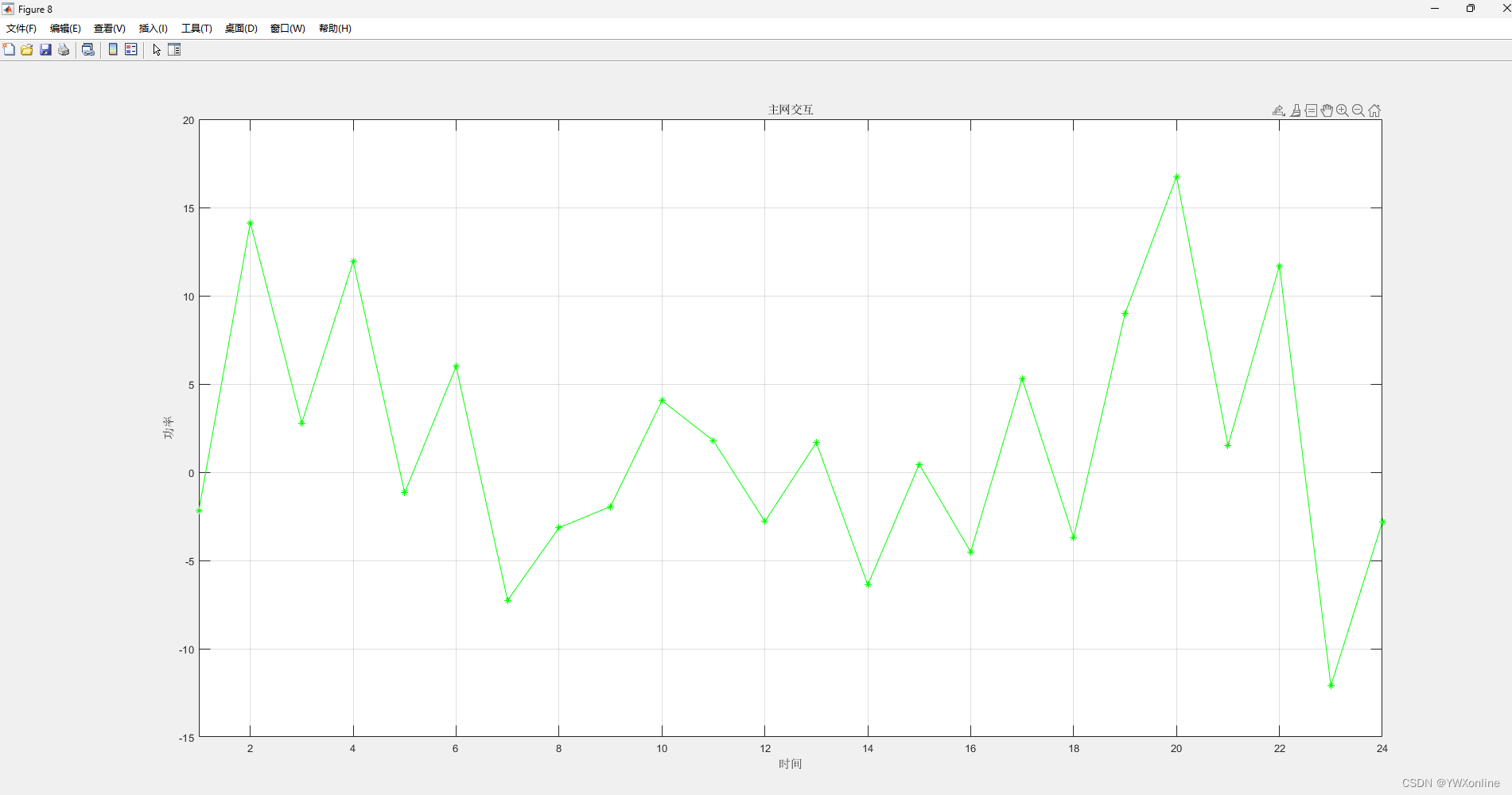
好啦,差不多就到这里了--------》文字,才是最高效的学习方式,视频可以作为科普,但是过了就过去了,多在论坛上,论文上逛一逛,受益更多一些。
代码的链接我放到这里了,大家自取自用
链接:https://pan.baidu.com/s/1JMSKbpWjsUKzNZy76-9YFQ
提取码:6666
后续我会更新改进的粒子群算法解读,希望对大家有帮助。