Pytorch实现简单的线性回归算法
简单 tensor的运算
Pytorch涉及的基本数据类型是tensor(张量)和Autograd(自动微分变量)
import torch
x = torch.rand(5, 3) #产生一个5*3的tensor,在 [0,1) 之间随机取值
y = torch.ones(5, 3) #产生一个5*3的Tensor,元素都是1
z = x + y #两个tensor可以直接相加
q = x.mm(y.transpose(0, 1)) #x乘以y的转置 mm为矩阵的乘法,矩阵相乘必须某一个矩阵的行与另一个矩阵的列相等
Tensor与numpy.ndarray之间的转换
import numpy as np #导入numpy包
a = np.ones([5, 3]) #建立一个5*3全是1的二维数组(矩阵)
b = torch.from_numpy(a) #利用from_numpy将其转换为tensor
c = torch.FloatTensor(a) #另外一种转换为tensor的方法,类型为FloatTensor,还可以使LongTensor,整型数据类型
b.numpy() #从一个tensor转化为numpy的多维数组
from torch.autograd import Variable # 导入自动梯度的运算包,主要用Variable这个类
x = Variable(torch.ones(2, 2), requires_grad=True) # 创建一个Variable,包裹了一个2*2张量,将需要计算梯度属性置为True
用pytorch做一个简单的线性关系预测
线性关系是一种非常简单的变量之间的关系,因变量和自变量在线性关系的情况下,可以使用线性回归算法对一个或多个因变量和自变量间的线性关系进行建模,该模型的系数可以用最小二乘法进行求解。生活中的场景往往会比较复杂,需要考虑多元线性关系和非线性关系,用其他的回归分析方法求解。
x = Variable(torch.linspace(0, 100, 100).type(torch.FloatTensor)) # 生成一些样本点作为原始数据
rand = Variable(torch.randn(100)) * 10 # 随机生成100个满足标准正态分布的随机数,均值为0,方差为1.将这个数字乘以10,标准方差变为10
y = x + rand # 将x和rand相加,得到伪造的标签数据y。所以(x,y)应能近似地落在y=x这条直线上
import matplotlib.pyplot as plt
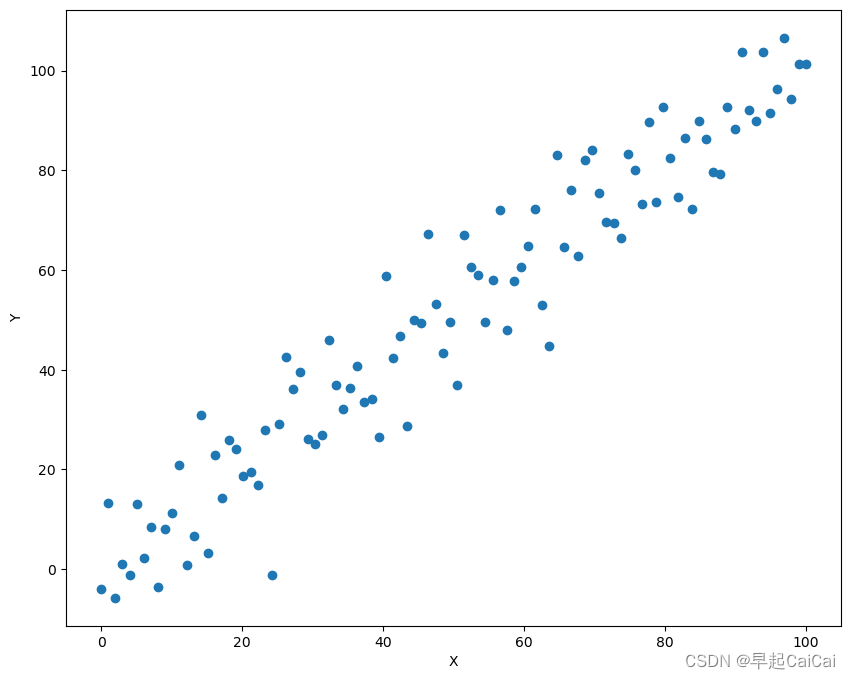
plt.figure(figsize=(10,8)) #设定绘制窗口大小为10*8 inch
plt.plot(x.data.numpy(), y.data.numpy(), 'o') #绘制数据,考虑到x和y都是Variable,需要用data获取它们包裹的Tensor,并专成numpy
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
构建模型
#a,b就是要构建的线性函数的系数
a = Variable(torch.rand(1), requires_grad = True) #创建a变量,并随机赋值初始化
b = Variable(torch.rand(1), requires_grad = True) #创建b变量,并随机赋值初始化
print('Initial parameters:', [a, b])
learning_rate = 0.0001 #设置学习率
for i in range(1000):
### 增加了这部分代码,清空存储在变量a,b中的梯度信息,以免在backward的过程中会反复不停地累加
if (a.grad is not None) and (b.grad is not None):
a.grad.data.zero_()
b.grad.data.zero_()
predictions = a.expand_as(x) * x+ b.expand_as(x) #计算在当前a、b条件下的模型预测数值
# 在 PyTorch 中,a.expand_as(x) 用于将张量 a 扩展(expand)为与张量 x 具有相同的形状
loss = torch.mean((predictions - y) ** 2) #通过与标签数据y比较,计算误差
print('loss:', loss)
loss.backward() #对损失函数进行梯度反传,backward的方向传播算法
a.data.add_(- learning_rate * a.grad.data) #利用上一步计算中得到的a的梯度信息更新a中的data数值
b.data.add_(- learning_rate * b.grad.data) #利用上一步计算中得到的b的梯度信息更新b中的data数值
绘制结果
x_data = x.data.numpy() # 将tensor 转为 numpy
plt.figure(figsize = (10, 7))
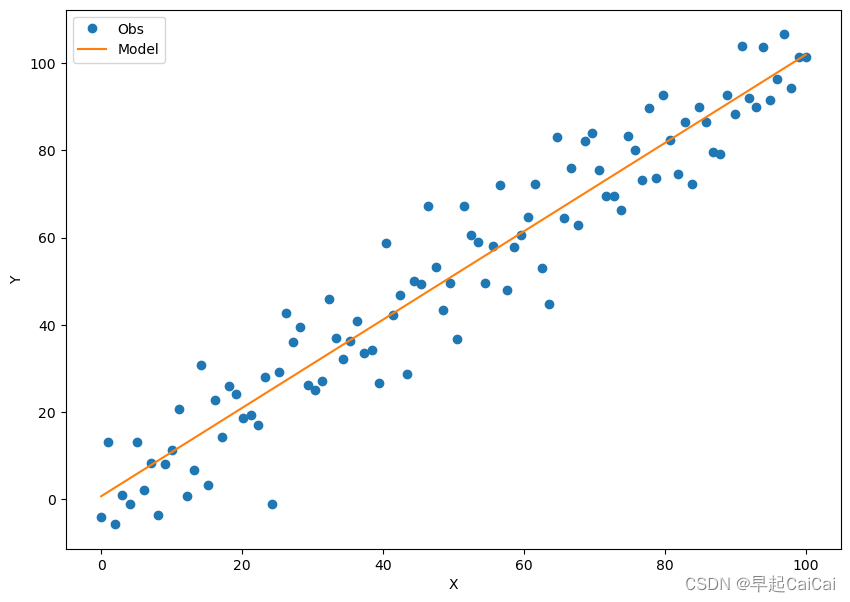
xplot = plt.plot(x_data, y.data.numpy(), 'o') # 绘制原始数据
yplot = plt.plot(x_data, a.data.numpy() * x_data + b.data.numpy()) #绘制拟合数据
plt.xlabel('X')
plt.ylabel('Y')
str1 = str(a.data.numpy()[0]) + 'x +' + str(b.data.numpy()[0]) # 图例信息 拟合的直线
plt.legend(['Obs', 'Model']) #绘制图例
plt.show()
x_test = Variable(torch.FloatTensor([1, 2, 10, 100, 1000])) #随便选择一些点1,2,……,1000
predictions = a.expand_as(x_test) * x_test + b.expand_as(x_test) #计算模型的预测结果
predictions #输出预测的数值