重点内容:
绪论:
简单的递推方程求解 1.19(1)(2) 、 教材例题
多个函数按照阶的大小排序 1.18
分治法:
分治法解决芯片测试问题
计算a^n的复杂度为logn的算法(快速幂)
分治法解决平面最近点对问题 (增加预处理)
锦标赛算法求第二大数的步骤(链表)
分治法S中第k小元素的归约过程 (m*)
动态规划:
最长公共子序列问题:蛮力法和动态规划的递归方程或递推关系、动态规划的伪码(填空)、优化函数和标记函数(填空)
矩阵链的乘法问题 : 蛮力法和动态规划的递归方程或递推关系、动态规划的伪码(填空)、备忘录和标记函数(填空)
最大子段和
贪心法:4.3 4.4 4.16 4.21
主要设计思想、伪码、复杂度、实例求解
贪心法:活动安排问题问题实例求解、最小延迟调度问题实例求解
回溯:
(填空)回溯算法的主要设计步骤,用回溯算法解决图的m着色问题、货郎问题(TSP)
(填空)分支界限的基本下,用分支界限算法解决最大团问题、背包问题
绪论:
多个函数按照阶的大小排序
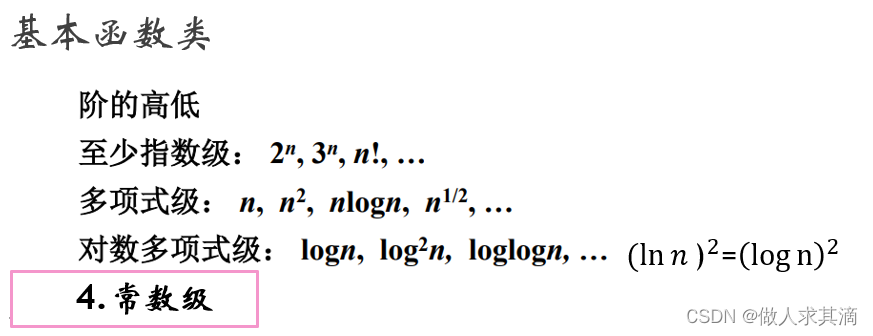
简单的递推方程求解
大小关系:指数级>多项式级>对数多项式级>常数级
化简:

主定理
【北大公开课】 算法设计与分析 屈婉玲教授 (76p)![]() https://www.bilibili.com/video/BV1Ls411W7PB/?p=16&share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8
https://www.bilibili.com/video/BV1Ls411W7PB/?p=16&share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8
教材例题
【北大公开课】 算法设计与分析 屈婉玲教授 (76p)![]() https://www.bilibili.com/video/BV1Ls411W7PB/?p=17&share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8
https://www.bilibili.com/video/BV1Ls411W7PB/?p=17&share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8
分治法:
分治法解决芯片测试问题
问题描述

一次测试过程:
两片都是好结果,就留一片。其他情况全丢掉

蛮力算法时间复杂度
 蛮力算法的判断好坏标准(一片芯片怎么判断好坏)
蛮力算法的判断好坏标准(一片芯片怎么判断好坏)
n为奇数情况

n为偶数情况

结论还是不变
分治法
假设 n为偶数,将 n片芯片两两一组做 测试淘汰,剩下芯片构成子问题,进 入下一轮分组淘汰。(类似锦标赛)


分治命题正确性


时间复杂度
主定理第三种情况ヽ(ー_ー)ノ直接记吧

计算a^n的复杂度为logn的算法(快速幂)
迭代伪码
输入:底数a,指数n
输出:计算完成的结果result
result=1; //用于存储结果
while p不为0时 do
if p为奇数
result =result *a //奇数需多乘一次底数
a=a*a;
n/=2;
递归伪码
输入:底数a,指数exponent
输出:计算完成的结果
function fastpow(a, exponent):
if exponent == 0
then return 1
if exponent == 1
then return a
temporary <- fastpow(a, exponent/2)
if exponent % 2 == 0
then return (temporary * temporary)
else
return (temporary * temporary * a)
时间复杂度

分治法解决平面最近点对问题 (增加预处理)
伪码

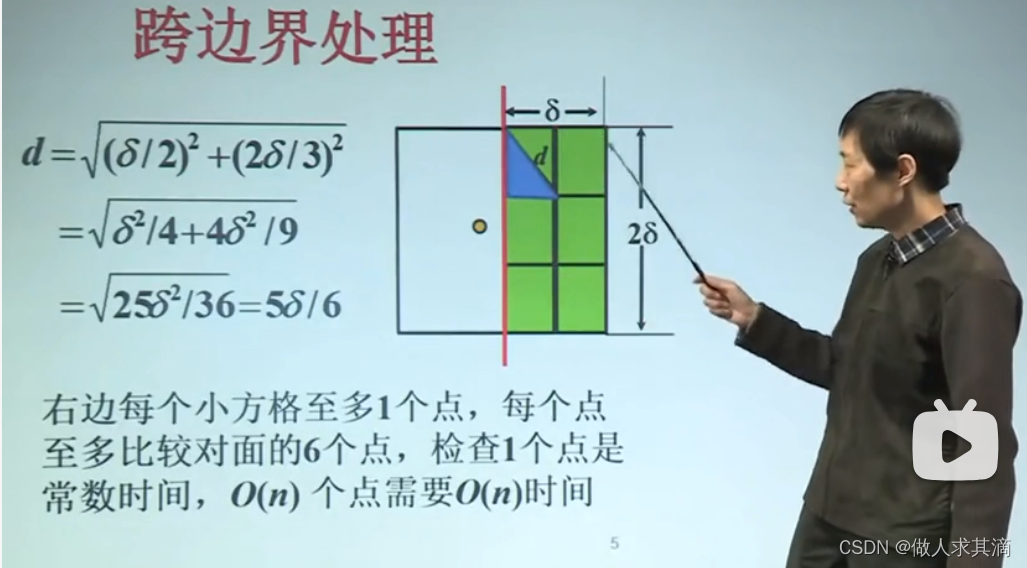 直接看课吧【【北大公开课】 算法设计与分析 屈婉玲教授 (76p)】
直接看课吧【【北大公开课】 算法设计与分析 屈婉玲教授 (76p)】![]() https://www.bilibili.com/video/BV1Ls411W7PB/?p=25&share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8
https://www.bilibili.com/video/BV1Ls411W7PB/?p=25&share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8
未改进的算法时间复杂度

改进:增加预处理

括号里面是第几个点,比如-2(3)就是横坐标x=-2,第p3点
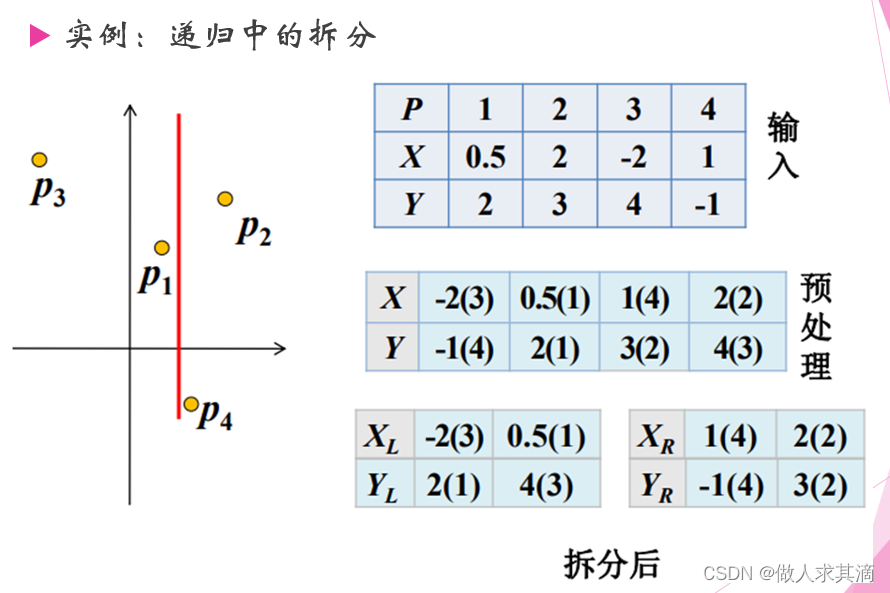
改进后算法的时间复杂度

锦标赛算法求第二大数的步骤(链表)
题目描述&蛮力算法时间复杂度

锦标赛算法

伪代码

7是第二小
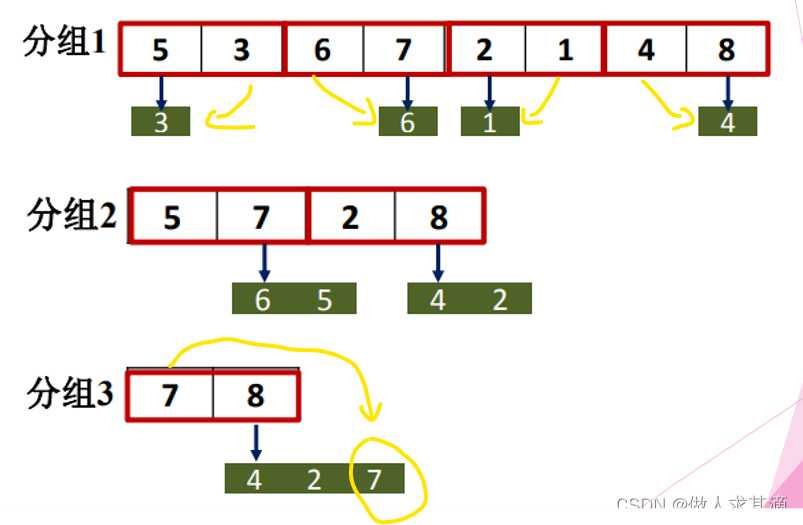
时间复杂度
算法比较分为两部分:第一部分是找最大元素max的比较次数,显然为n-1;第二部分是在产生max后链表中找最大所需的比较次数。

分治法S中第k小元素的归约过程 (m*)
问题描述

简单的算法(k次最小算法 or 排序后输出)

分治算法
每一组就是一列,先排序,上面大下面小
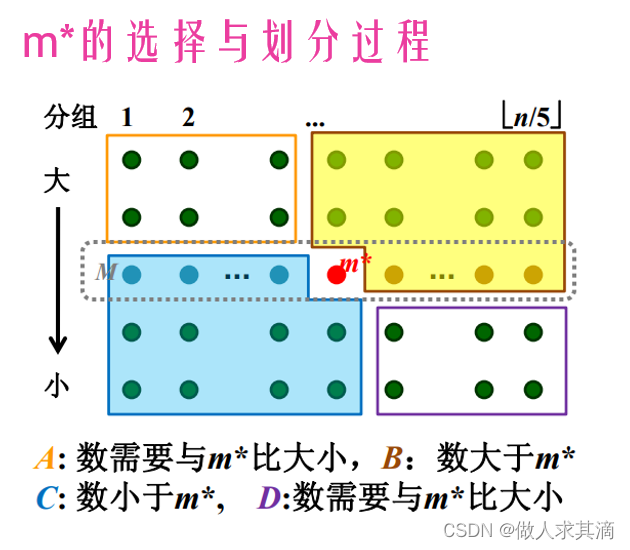
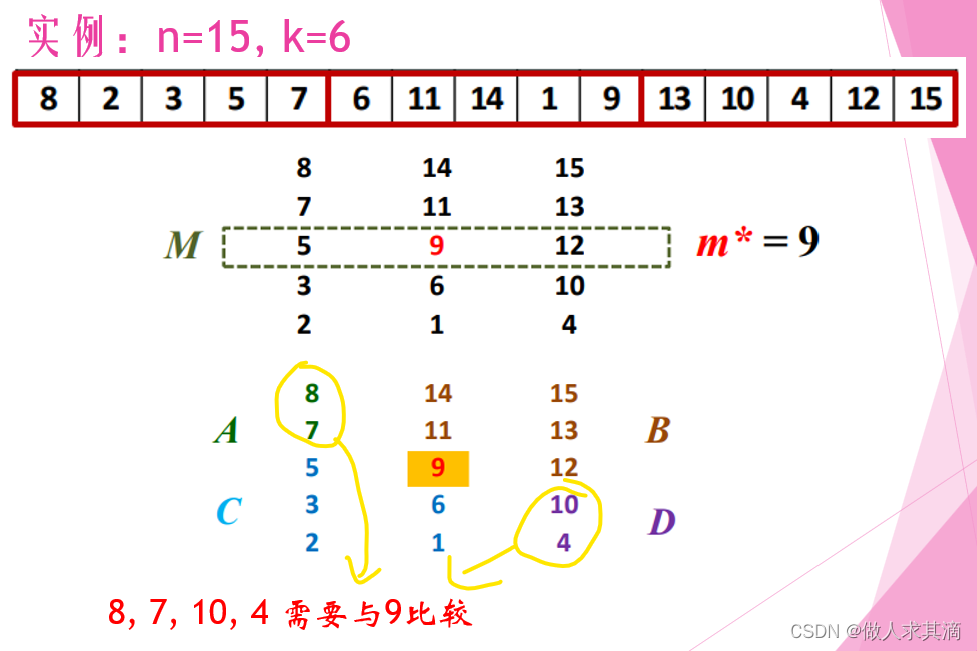
8,7,10,4不确定大小,所以要和m*比较
伪代码

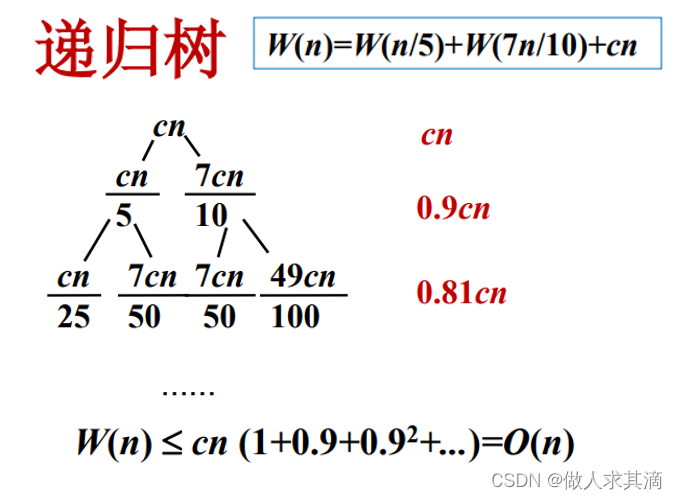
时间复杂度
动态规划:
最长公共子序列问题:
蛮力法的时间复杂度O(n*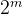 )
)

#include <iostream>
#include <string>
using namespace std;
string lcs_bruteforce(const string& X, const string& Y) {
int m = X.length();
int n = Y.length();
if (m == 0 || n == 0) {
return "";
} else if (X[m-1] == Y[n-1]) {
return lcs_bruteforce(X.substr(0, m-1), Y.substr(0, n-1)) + X[m-1];
} else {
string lcs1 = lcs_bruteforce(X.substr(0, m-1), Y);
string lcs2 = lcs_bruteforce(X, Y.substr(0, n-1));
if (lcs1.length() > lcs2.length()) {
return lcs1;
} else {
return lcs2;
}
}
}
int main() {
string X = "ABCBDAB";
string Y = "BDCAB";
string lcs = lcs_bruteforce(X, Y);
cout << "The longest common subsequence is: " << lcs << endl;
return 0;
}参考代码
动态规划的递归方程或递推关系

✨代码实现:
【算法设计与分析MOOC-青岛大学-张公敬教授】![]() http:// https://www.bilibili.com/video/BV18X4y1k74c/?p=27&share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8
http:// https://www.bilibili.com/video/BV18X4y1k74c/?p=27&share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8
动态规划的伪码(填空)


优化函数(填空)
X = 【1, 2, 3】, Y = 【1, 3】按照下图关系推
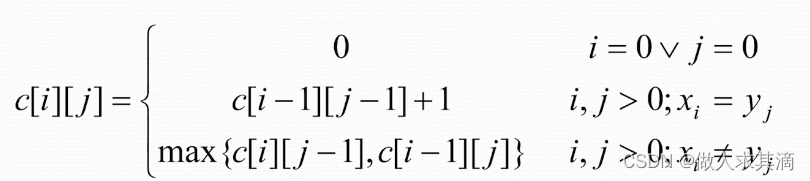
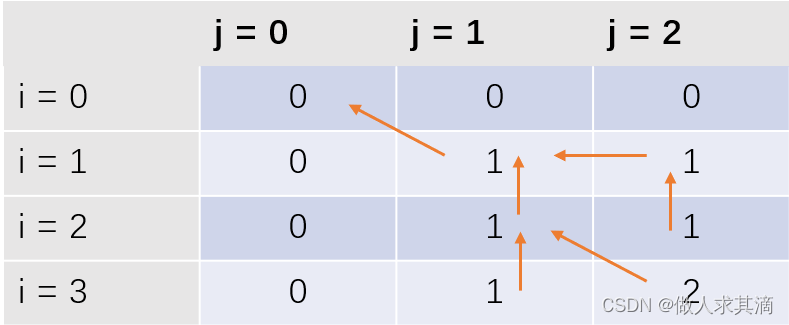
标记函数(填空)
b数组用来设立标记,算法结束后可以利用这些标记追踪最优解。

例子:
 怎么推?
怎么推?
c[i][j]矩阵:
 按照信息表即可推出b矩阵(数组)
按照信息表即可推出b矩阵(数组)

如何追踪解?
b[i][j]为1时,对应X、Y序列第i行,j列中的元素
矩阵链的乘法问题:
蛮力法的时间复杂度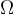 (
( )
)

动态规划的递归方程或递推关系


动态规划的伪码(填空)
递归实现:

时间复杂度

迭代实现:

备忘录(填空)
看着递推方程来填空


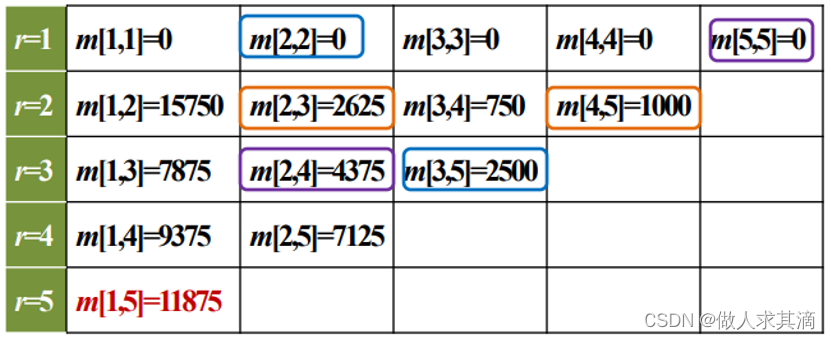
自己复制代码,断点调试设置变量查看吧
#include <bits/stdc++.h>
using namespace std;
//输入:矩阵链Ai…j的输入为向量P=<Pi-1,Pi,…,Pj>,其中:1<=i<=j<=n.
//输出:计算Ai…j的所需最小乘法运算次数m[i,j]和最后一次运算位置s[i,j]。
const int N = 101;
int m[N][N], s[N][N];
int a[] = {30, 35, 15, 5, 10, 20};
void MatrixChain(int a[N], int n)
{
for(int i=1; i<=n; i++)
m[i][i] = 0;
for(int r=2; r<=n; r++)
{
for(int i=1; i<= n-r+1; i++)
{
int j = i+r-1;
m[i][j] = m[i+1][j] + a[i-1]*a[i]*a[j];
s[i][j] = i;
for(int k=i; k<=j-1; k++)
{
int t = m[i][k] + m[k+1][j] + a[i-1]*a[k]*a[j];
if(t < m[i][j])
{
m[i][j] = t;
s[i][j] = k;
}
}
}
}
}
int main()
{
MatrixChain(a, 6);
cout << "The number of least multiplication operations:" << endl;
cout << m[1][5] << endl;
cout << "Position of the last operation:" << endl;
cout << s[1][5] << endl;
cout << "array s:" << endl;
for(int i=1; i<=5; i++)
{
for(int j=1; j<=5; j++)
{
cout << s[i][j] << ' ';
}
cout << endl;
}
return 0;
}标记函数(填空)
记录k的值,k就是分割线
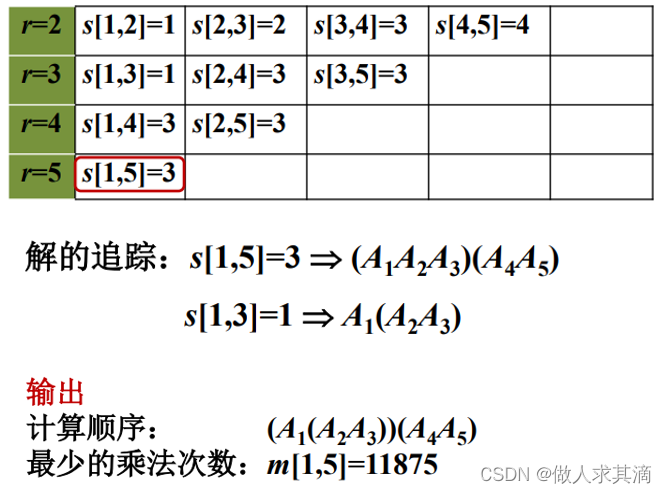
最大子段和
力扣(LeetCode)53.最大子数组和
蛮力算法O(n^2--n^3)
O()

改进后O()

分治算法O(nlogn)
思路:一路分分分,分到只有左边一个和右边一个的时候开始计算。分治区间左右两半分别求和放好(leftsum, rightsum),还有一个跨边界,把边界左边(整个数组第一个元素)和右边(整个数组最后一个元素)全加起来
分治区间:当前递归函数所计算的左右区间


代码:

————————————————
版权声明:图片为博主原创文章摘录
链接:https://blog.csdn.net/weixin_73523694/article/details/134515793
动态规划算法
类似前缀和思想,判断前一个数是否大于0,不是就不加,是就加,当前数+前一个数。以达到最大和的目的


时间复杂度O(n),空间复杂度O(n)
伪代码写成代码:
int MaxInterval(vector<int> a, int len) {
vector<int> dp(len);
int res = -INF;
dp[0] = a[0];
for(int i = 1; i < len; i ++ ) {
dp[i] = max(a[i], dp[i - 1] + a[i]);
res = max(res, dp[i]);
}
return res;
}贪心法:
4.3

最坏情况下的时间复杂度函数
主要设计思想、伪码、复杂度、实例求解
这是一个经典的区间覆盖问题,可以通过贪心算法来解决。我们的目标是用最少的基站覆盖所有房子,且每个房子都在至少一个基站的4千米范围内。
主要设计思想
1. 贪心策略:为了覆盖最多的房子,每次选择可以覆盖尚未被覆盖的房子中最远的那个房子的位置作为新基站的位置。这样可以确保每个新基站都能覆盖最多未被覆盖的房子。
2. 迭代过程:从房子A开始,依次考虑每个房子,如果当前房子不在已有基站的覆盖范围内,则在其位置设置新的基站。
3. 覆盖检查:对于每个房子,检查是否已经在任意基站的4千米范围内。如果是,则该房子已被覆盖;如果不是,则需要在新的位置设置基站。
伪码
输入:房子距离A的列表distances[1...n]
输出:基站位置列表base_stations
初始化基站位置列表base_stations为空
对房子距离A的列表进行升序排序
for i = 1 to n do
基站位置列表base_stations添加设置新基站位置distances[i]+4
rightpoint <- distances[i]+8
在房子距离A的列表distances中寻找大于rightpoint的点
end for
返回base_stations
时空复杂度分析
时间复杂度:最坏情况下,我们需要遍历所有的房子来检查是否已经被覆盖,因此时间复杂度为O(n),其中n是房子的数量。
空间复杂度:除了输入的距离列表,我们还需要存储基站位置列表,因此空间复杂度为O(n)。
实例求解
假设房子到A的距离分别是[0, 5, 10, 15]千米。按照上述算法:
1. 从房子A开始,设置基站1(位置0+4千米),覆盖范围[0, 8]千米。房子B(位置5千米)在覆盖范围内。
2. 房子C(位置10千米)不在覆盖范围内,设置基站2(位置10+4千米),覆盖范围[10, 18]千米。房子D(位置15千米)在覆盖范围内。
最终基站位置为[4,14]千米。
这个算法通过贪心策略确保了使用最少数量的基站来覆盖所有的房子,同时满足每个房子都在至少一个基站的4千米范围内。
4.4
题目:

主要设计思想、伪码、复杂度、实例求解
这是一个典型的区间覆盖问题,我们可以通过贪心算法来解决这个问题。算法步骤如下
设计思想
由于点已经按照从小到大的顺序排列,我们可以直接从最小的点开始,每次都尽可能选择包含更多未被覆盖的点的闭区间。具体步骤如下:
1. 初始化闭区间集合为空,当前覆盖的点集也为空。
2. 从未被覆盖的点中选择最小的一个作为新闭区间的左端点。
3. 向右扩展这个长度为1闭区间直到不能覆盖更多的点为止。
4. 将这个闭区间加入到闭区间集合中,记录个数和位置,并将覆盖的点标记为已覆盖。
5. 重复步骤2-4,直到所有的点都被覆盖。
伪码
输入:点集x1, x2, ....., xn
输出:闭区间集合初始化闭区间集合S为空
for i=1 to n do
选择未被覆盖的最小点x_i
设置闭区间右端点right <- x_i + 1
while x_i+1 < right do
i <- i+1; (i++的意思)
将[x_i, right]添加到Send for
时空复杂度分析
时间复杂度:算法需要遍历所有的点来确定每个闭区间,因此时间复杂度为O(n),其中n是点的数量。
空间复杂度:除了输入的点集外,我们需要存储每个闭区间集合位置,因此空间复杂度也是O(n)。
实例求解
假设给定的点集为{1,2,3,7,8,9},按照上述算法:
- 对于点1,2,闭区间是[1, 2]
- 对于点3,闭区间是[3, 4]
- 对于点7,8,闭区间是[7, 8]
- 对于点9,闭区间是[9, 10]
最终得到的闭区间集合是{[1,2],[3,4],[7,8],[9,10]},闭区间个数4个。覆盖了所有的点。
这个算法确保了每个点都被一个长度为1的闭区间覆盖,满足了题目的要求。
4.16

主要设计思想、伪码、复杂度、实例求解
设计思想:双指针算法
算法的核心思想是利用两个指针分别遍历序列A和B。由于B是A的子序列,因此B中的每个元素都必须按顺序出现在A中。我们可以通过比较两个序列当前指针所指向的元素来检查这一点。如果B的当前元素与A的当前元素匹配,则将B的指针向前移动一位;无论是否匹配,A的指针都向前移动一位。如果B的指针移动到了序列末尾,说明B是A的子序列。
伪码:
算法4.16 IsSubsequence
输入:A、B两个序列
输出:如果B是A的子序列,输出True;否则返回False
i <- 0
j <- 0
while i < n and j < m do
if A[i] == B[j] then
j <- j+1
i <- i+1
if j == m then
Return True
else
Return False
时空复杂度分析:
时间复杂度为O(n),因为最坏的情况下,我们需要遍历整个A序列一次。
空间复杂度为O(1),因为我们只使用了常数个辅助变量。
实例求解:
假设A = [1, 2, 3, 4, 5],B = [2, 4]。
- 初始化i = 0, j = 0。
- 比较A[0]与B[0],不匹配,i = 1。
- 比较A[1]与B[0],匹配,i = 2, j = 1。
- 比较A[2]与B[1],不匹配,i = 3。
- 比较A[3]与B[1],匹配,i = 4, j = 2。
- 此时j已经等于B的size,说明B是A的子序列。
因此,算法判断B是A的子序列是正确的。
4.21
题目:

主要设计思想、伪码、复杂度、实例求解
设计思想:
这个问题可以通过求解所有集合的交集来找到最小的集合S,使得每个A$_{i}$至少含有S中的一个数。由于每个集合A$_{i}$是由连续的正整数构成的,我们可以通过比较相邻集合的边界来逐步缩小交集的范围,直到找到最小的满足条件的集合S。
伪码:
算法4.21 FindSmallestSet(A)
输入:n个集合A1,...,An。
输出:最小的满足条件的集合S。
对n个集合的右端点进行升序排序
for i <- 1 to n do
选一个集合A[i]作为一个交集,加入S
j <- i+1
while A[j]的左断点小于当前交集右端点 do
删除A[j]
j <- j+1
时空复杂度分析:
时间复杂度为O(nlogn),因为需要对集合进行排序。
空间复杂度为O(n),用于存储集合S。
实例求解:
假设有集合 A1 = [1, 3], A2 = [2, 6], A3 = [7, 10], A4 = [8, 9]。
- 对n个集合的右端点进行升序排序,A1,A2,A4,A3。
- 选择A1,加入S中。由于A2左端点小于A1右端点,所以删除A2
- 选择A4,加入S中。由于A3左端点小于A4右端点,所以删除A3
- 返回S = {A1, A4}作为最小集合,满足每个Ai至少含有S中的一个数。
活动安排问题实例求解
如果第二个活动的开始时间大于第一个活动的结束时间,就加入集合A

先按照起始时间排序

最小延迟调度问题实例求解
题目P91


回溯:
回溯算法的主要设计步骤

用回溯算法解决图的m着色问题

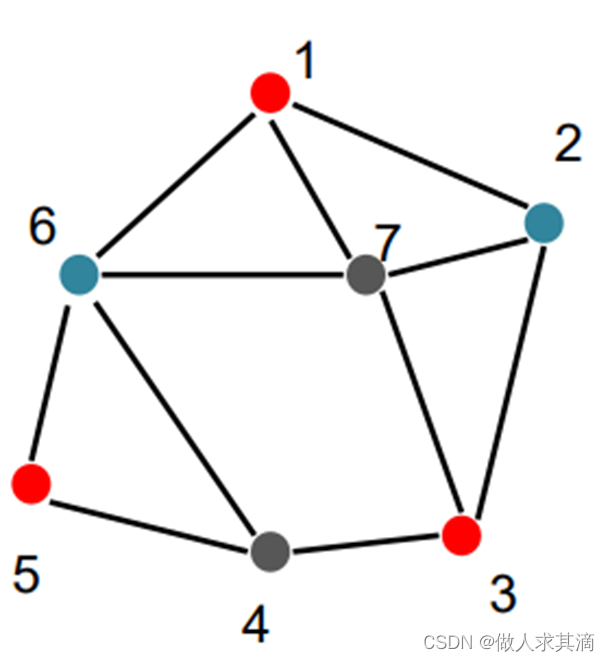
搜索策略:深度优先
时间复杂度O(n)
第一个解向量:< 1, 2, 1, 3, 1, 2, 3 >。根据对称性,只需搜索 1/3 的解空间. 当点1和点2确定, 即 以后,只有1个解,点2为根的子树中也只有1个解。由于3个子树的对称性,总共6个解。
对称性:3的地方换成2,2的地方换成3
货郎问题(TSP)旅行售货员问题
定义(题目)

解向量 & 约束条件 & 搜索空间(子结点排列规则)

【【北大公开课】 算法设计与分析 屈婉玲教授 (76p)】
太多不更了,看视频吧
分支限界
相关概念
目标函数(极大化或极小化)
约束条件(解满足的条件)
可行解: 搜索空间满足约束条件的解
最优解: 使得目标函数达到极大 (或极小)的可行解


用分支限界算法解决最大团问题
题目
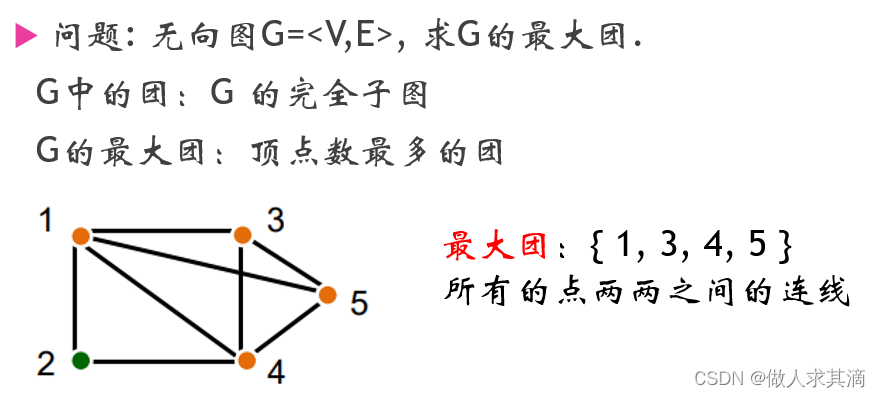
代价函数

实例

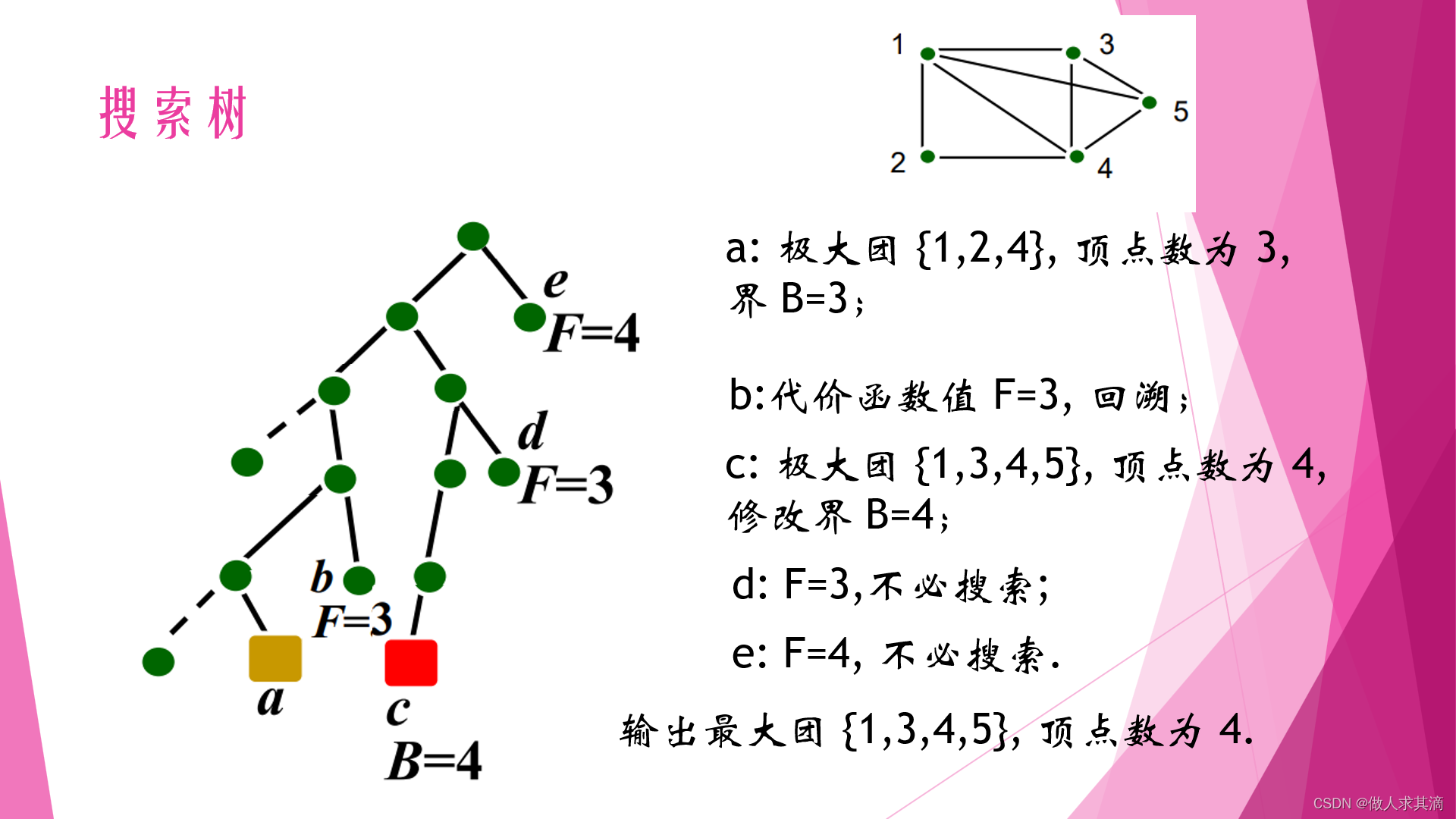
来不及就直接背吧
用分支限界算法解决背包问题
题目:


代价函数
是理想情况下,每一个小空隙都装第k+1件物品。实际情况是第k+1件物品塞不满这些空隙的

分支策略:深度优先
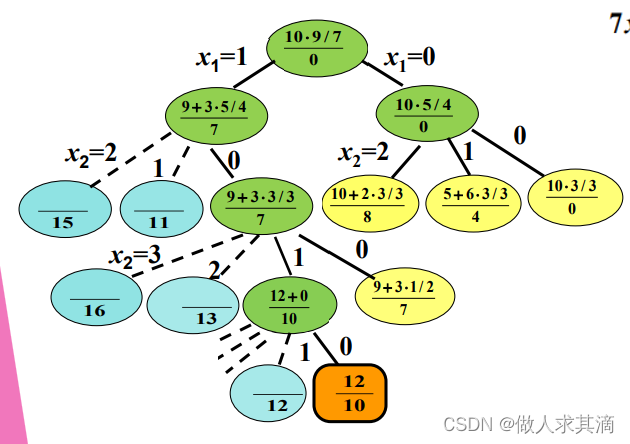
界函数
界函数初始值0,到达橙色框后得到了更好的可行解,就更新界函数的值为12。
之后的深度搜索中,当代价函数大于界函数时,继续向下搜索。当代价函数小于界函数时,就可以停止向前了,因为往下也得不到更好的,这已经是下面的叶子结点中最大的一个代价函数值