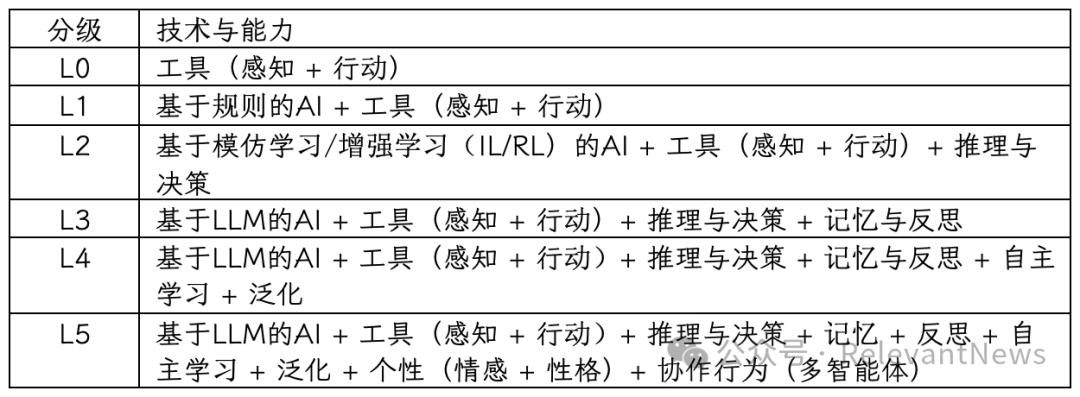
目录

固定效应

---

固定效应

为了方面后面更正式地讲述，让我们首先看一下我们拥有的数据。按照我们的例子，我们将尝试估计婚姻对收入的影响。我们的数据包含多年以来多个个体 (nr) 的这两个变量，married 和lwage。请注意，工资采用对数形式。除此之外，我们还有其他控制措施，例如当年的工作小时数、受教育年限等。

from linearmodels.datasets import wage_panel
data = wage_panel.load()
data.head()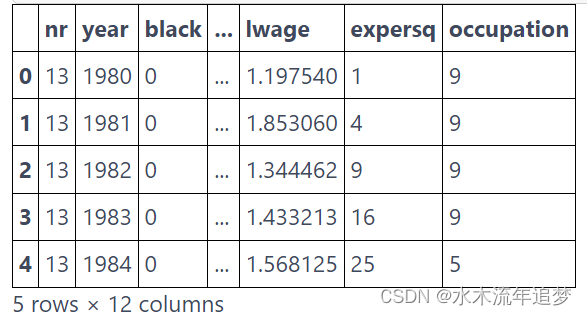

通常，固定效应模型定义为

其中 是个体 i 在时间 t 的结果， 是个体变量的向量i 在时间 t。  是单个 i 的一组不可观测值。请注意，这些不可观测值随着时间的推移是不变的，因此缺少时间下标。最后， 是错误项。对于教育示例， 是对数工资， 是随时间变化的可观察变量，例如婚姻和经验，是每个人没有观察到但不变的变量，例如美丽和智力。

现在，请记住我说过使用具有固定效果模型的面板数据就像为实体添加虚拟对象一样简单。这是真的，但在实践中，我们实际上并没有这样做。想象一个我们有 100 万客户的数据集。如果我们为它们中的每一个添加一个 dummy，我们最终会得到 100 万列，这可能不是一个好主意。相反，我们使用将线性回归划分为 2 个独立模型的技巧。我们以前见过这个，但现在是回顾它的好时机。假设您有一个线性回归模型，其中包含一组特征  和另一组特征 。

其中  和  是特征矩阵（每个特征一行，每个观察一列）和  和  是行向量。您可以通过执行获得完全相同的  参数

1. 在第二组特征  上回归结果 y
2. 在第二个  上回归第一组特征
3. 得到残差  和 
4. 将结果的残差回归到特征残差 

最后一次回归的参数将与使用所有特征运行回归完全相同。但这究竟对我们有什么帮助呢？好吧，我们可以将带有实体假人的模型的估计分解为 2。首先，我们使用假人来预测结果和特征。这些是上面的步骤 1 和 2。

现在，还记得在虚拟变量上运行回归是如何像估计该虚拟变量的平均值一样简单吗？如果你不这样做，让我们用我们的数据来证明这是真的。让我们运行一个模型，我们将工资预测为虚拟年份的函数。

mod = smf.ols("lwage ~ C(year)", data=data).fit()
mod.summary().tables[1]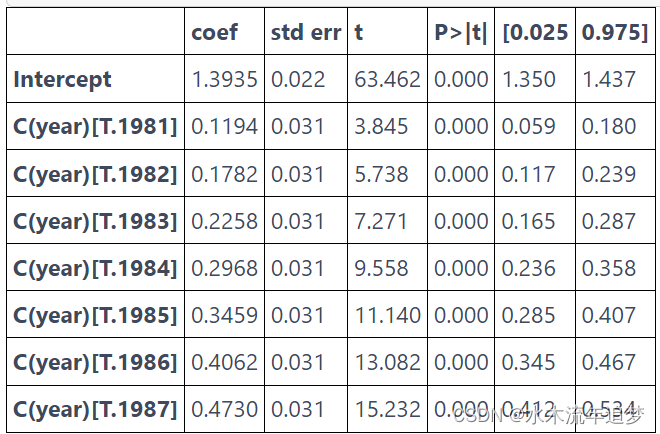

请注意该模型如何预测 1980 年的平均收入为 1.3935，1981 年的平均收入为 1.5129 (1.3935+0.1194) 等等。 现在，如果我们按年份计算平均值，我们会得到完全相同的结果。 （请记住，基准年 1980 是截距。因此，您必须将截距添加到其他年份的参数中才能获得该年的平均lwage）。

data.groupby("year")["lwage"].mean()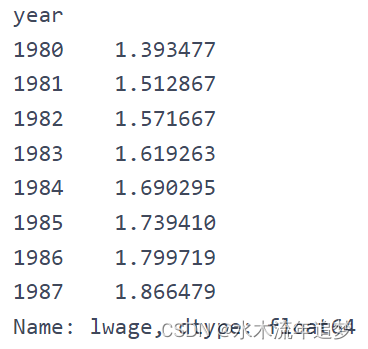

这意味着，如果我们得到面板中每个人的平均值，我们基本上是在对其他变量进行个体虚拟回归。这激发了以下估计过程：

1. 通过减去个人的平均值来创建时间贬损变量：

2. 在 上回归上回归

请注意，当我们这样做时，未观察到的  消失了。由于  在时间上是恒定的，所以我们有 。如果我们有以下两个方程组

我们从另一个中减去一个，我们得到

它消除了所有未观察到的随时间不变的事物。老实说，不仅未观察到的变量消失了。这发生在所有时间不变的变量上。因此，您不能包含任何随时间保持不变的变量，因为它们将是虚拟变量的线性组合，并且模型不会运行。

要检查哪些变量是这些变量，我们可以按个体对数据进行分组并获得标准差的总和。如果它为零，则意味着对于任何个人来说，变量都不会随时间变化。

data.groupby("nr").std().sum()
year            1334.971910
black              0.000000
exper           1334.971910
hisp               0.000000
hours         203098.215649
married          140.372801
educ               0.000000
union            106.512445
lwage            173.929670
expersq        17608.242825
occupation       739.222281
dtype: float64

对于我们的数据，我们需要删除实体假人，black和hisp，因为它们对于个人来说是恒定的。 此外，我们需要取消教育。 我们也不会使用职业，因为这可能会调节婚姻对工资的影响（可能是单身男性能够承担更多时间要求更高的职位）。 选择了我们将使用的功能后，是时候估计这个模型了。

要运行我们的固定效应模型，首先，让我们获取平均数据。 我们可以通过按个人对所有内容进行分组并取平均值来实现这一点。

Y = "lwage"
T = "married"
X = [T, "expersq", "union", "hours"]

mean_data = data.groupby("nr")[X+[Y]].mean()
mean_data.head()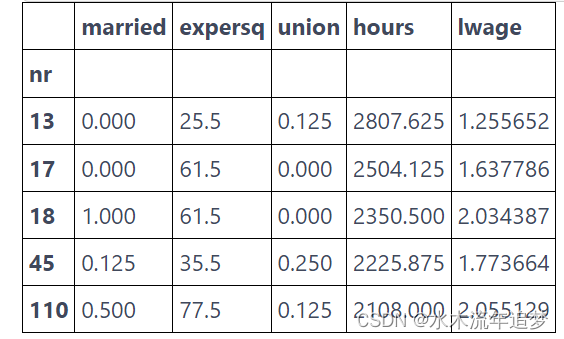

为了将数据围绕均值标准化（demean），我们需要将原始数据的索引设置为个体标识符，nr。 然后，我们可以简单地从一个数据集中减去对应的数据均值的数据集。

demeaned_data = (data
               .set_index("nr") # set the index as the person indicator
               [X+[Y]]
               - mean_data) # subtract the mean data

demeaned_data.head()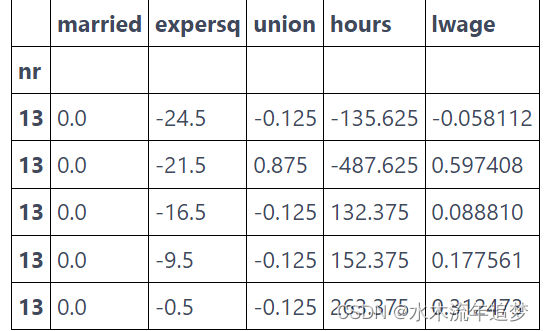

mod = smf.ols(f"{Y} ~ {'+'.join(X)}", data=demeaned_data).fit()
mod.summary().tables[1]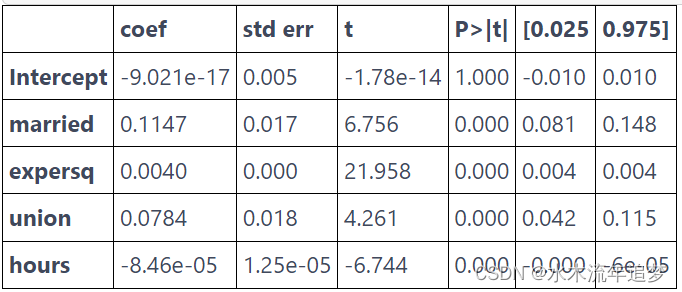

如果我们相信固定效应消除了所有遗漏的变量偏差，那么这个模型告诉我们婚姻使男人的工资增加了 11%。 这个结果非常显着。 这里的一个细节是，对于固定效应模型，需要对标准误差进行聚类。 因此，我们可以使用库 linearmodels 并将参数 cluster_entity 设置为 True，而不是手动进行所有估计（这只是出于教学原因）。

from linearmodels.panel import PanelOLS
mod = PanelOLS.from_formula("lwage ~ expersq+union+married+hours+EntityEffects",
                            data=data.set_index(["nr", "year"]))

result = mod.fit(cov_type='clustered', cluster_entity=True)
result.summary.tables[1]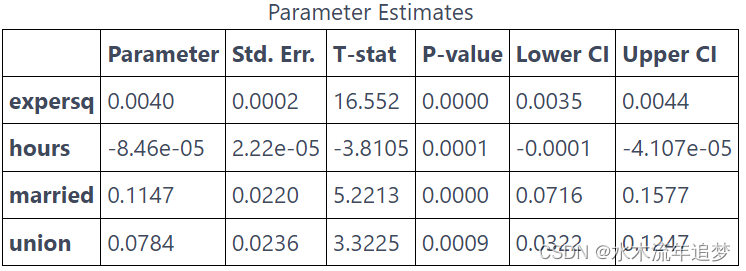

mod = smf.ols("lwage ~ expersq+union+married+hours+black+hisp+educ", data=data).fit()
mod.summary().tables[1]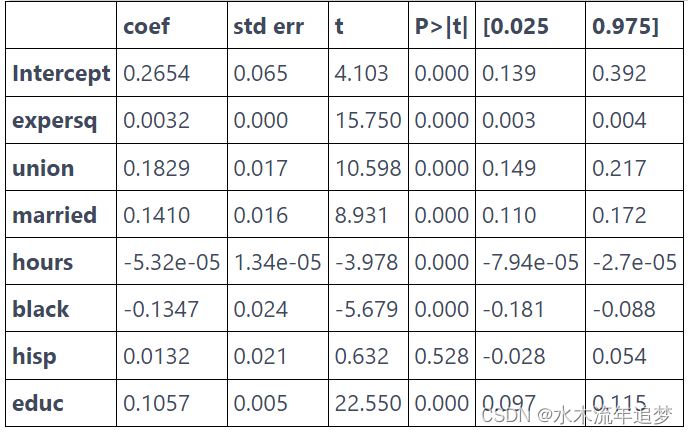

这个模型是说婚姻使男人的工资增加了 14%。 比我们在固定效应模型中发现的效应要大一些。 这表明由于固定的个体因素（如智力和美貌）没有被添加到模型中，结果存在一些省略变量偏差。