引言
多重背包,相对于01背包来说,多重背包是每个物品会有相应的个数,最多可以选那么多个,因而对于朴素多重背包,需要在01背包的基础上,再加一层物品的循环
朴素多重背包例题
P2347 [NOIP1996 提高组] 砝码称重

题意,就是说有六种砝码每种砝码有自己的个数,问你能达到的重量搭配是多少
题解:标准的多重背包,我们可以用dp[ j ]去表示 j 重量能否达到,如果能达到就是1,如果不能打达到就是0,最后遍历一遍dp数组去判断有多少个1即可
#include<bits/stdc++.h>
using namespace std;
int a[7];
int w[7]={0,1,2,3,5,10,20};
int dp[1050];
int main()
{
for(int i=1;i<=6;i++)
cin>>a[i];
dp[0]=1;
for(int i=1;i<=6;i++)
{
for(int j=1050;j>=0;j--)
{
for(int k=0;k<=a[i];k++)//遍历第i个物品选的个数
{
if(dp[j]==1)
{
dp[j+k*w[i]]=1;
}
}
}
}
int sum=0;
for(int i=1;i<=1000;i++)
if(dp[i]!=0)
sum++;
cout<<"Total="<<sum;
return 0;
}P6771 [USACO05MAR] Space Elevator 太空电梯
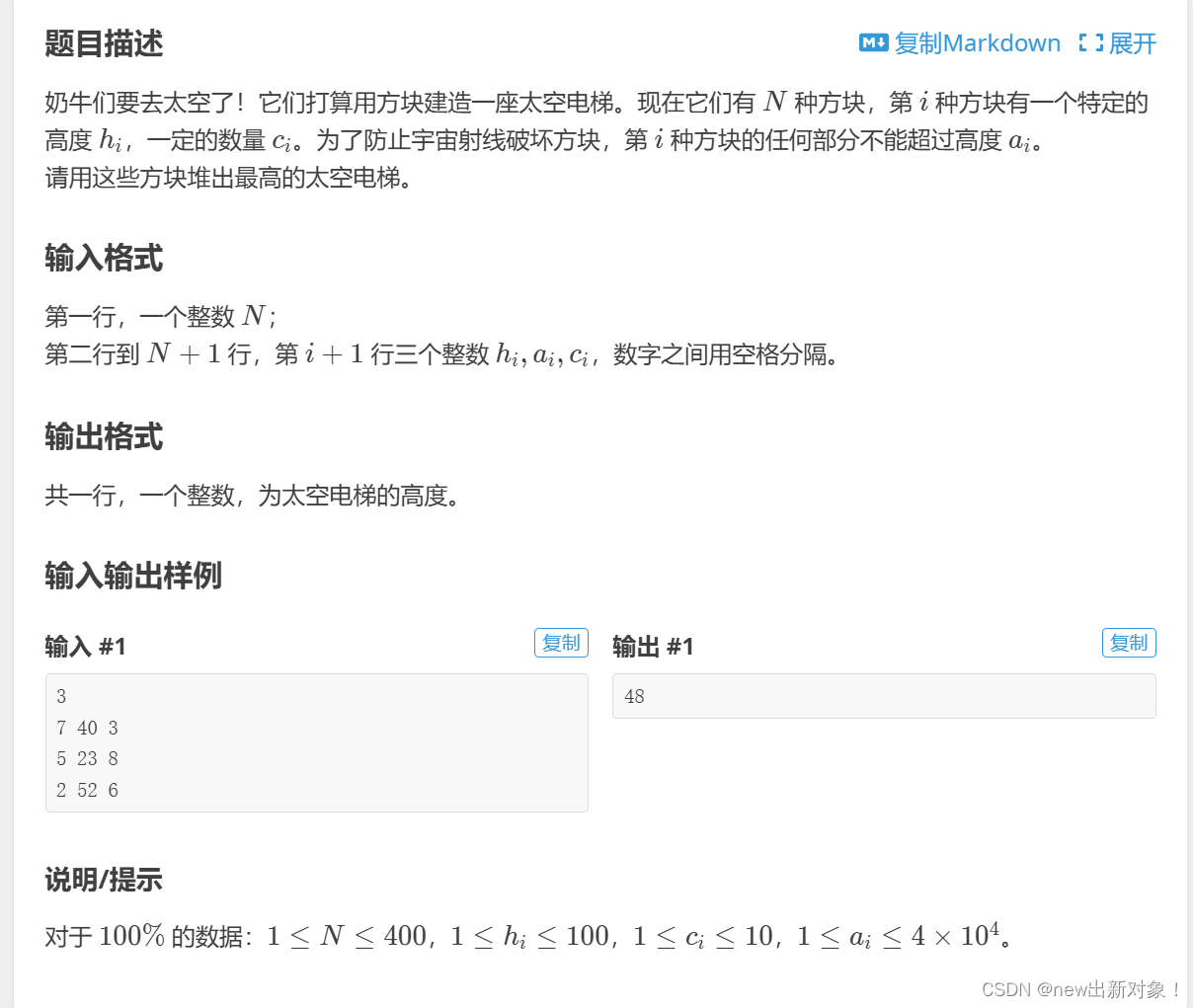
题意,就是说给你n中方块,每个方块有自己的高度,和最大搭建的限制(在某个高度以后不能用这种方块),还有方块的数量
思路:这是一个变式,我们需要将其组装成一个结构体,然后对a数组进行排序,从小到大进行排序,然后进行多重背包即可
#include<bits/stdc++.h>
using namespace std;
int n;
struct node{
int h;
int limit;
int num;
}a[405];
int dp[40005];//能否达到高度为j,能达到为1,不能为0
bool cmp(node a,node b)
{
return a.limit<b.limit;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i].h>>a[i].limit>>a[i].num;
dp[0]=1;
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++)
{
for(int j=a[i].limit;j>=0;j--)
{
for(int k=0;k<=a[i].num&&j+k*a[i].h<=a[i].limit;k++)
{
if(dp[j]==1)
{
dp[j+k*a[i].h]=1;
}
}
}
}
for(int i=a[n].limit;i>=0;i--)
{
if(dp[i]==1)
{
cout<<i;
return 0;
}
}
return 0;
} P5365 [SNOI2017] 英雄联盟

题意:有n个英雄,每个英雄有k个皮肤,对于一个英雄的所有皮肤都是一个价格c,但是我又想要m中搭配,正常的求法是算出m个搭配至少要多少钱,但是这题m的数据太大了,只能通过对于一定的钱,其搭配数是多少
思路:dp数组表示的是对于j元,总共有多少的搭配数,然后判断这个搭配数是否大于m从前向后遍历,找到第一个大于m种搭配的位置,那个下标就是最小花费
//英雄联盟
//这题皮肤搭配数量太大了,肯定不能当数组,要换成j个q币能搞得最大皮肤搭配
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
int num[135];
int w[135];
int dp[270005];
signed main()
{
cin>>n>>m;
int sum=0;//计算总金额
for(int i=1;i<=n;i++)
{
cin>>num[i];
}
for(int i=1;i<=n;i++)
{
cin>>w[i];
sum+=num[i]*w[i];
}
dp[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=sum;j>=0;j--)
{
for(int k=0;k<=num[i]&&k*w[i]<=j;k++)
{
dp[j]=max(dp[j],dp[j-k*w[i]]*k);
}
}
}
for(int i=1;i<=sum;i++)
{
if(dp[i]>=m)
{
cout<<i;
return 0;
}
}
return 0;
}二进制优化
用到的是二进制拆分思想
比如说对于50这个数,我们用二进制拆分可以分为 1,2,4,8,16,19,这五个数,我们这五个数搭配可以组成50以内的所有自然数,所以我们二进制优化也是通过拆分每个物品的个数从而降低时间复杂度,从而形成完全的01背包问题
二进制优化例题
P1776 宝物筛选

一看这道题,如果用正常的多重背包,时间复杂度为100*40000*100000肯定会爆数据的,所以我们要用二进制优化,将时间复杂度变为4e6*log2(100000),这样就大大降低的时间的复杂度
将物品数量进行二进制拆分
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
int v[1405];
int w[1405];
int dp[40005];
signed main()
{
cin>>n>>m;
int vv,ww,mm;
int cnt=0;
for(int i=1;i<=n;i++)
{
cin>>vv>>ww>>mm;
for(int j=1;j<=mm;j<<=1)
{
cnt++;
v[cnt]=j*vv;
w[cnt]=j*ww;
mm-=j;
}
if(mm)
{
cnt++;
v[cnt]=mm*vv;
w[cnt]=mm*ww;
}
}
for(int i=1;i<=cnt;i++)
{
for(int j=m;j>=w[i];j--)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout<<dp[m];
return 0;
}