个人主页：仍有未知等待探索-CSDN博客

专题分栏：C++

目录

一、概念

性质

二、操作 

插入

情况一：cur为红、p为红、g为黑，如果u存在且为红

步骤：

情况二：cur为红、p为红、g为黑，如果u不存在或者u存在且为黑 

情况a步骤：

情况b步骤：

情况三：cur为红、p为红、g为黑，如果u不存在或者u存在且为黑 

步骤：

 三、总代码

---

一、概念

红黑树是一颗特殊的二叉搜索树。红黑树虽然不要求是平衡的，但是该树的最长路径不超过最短路径的二倍。

红黑树避免了过多的旋转问题。

性质

1、每个节点的颜色不是红色就是黑色。

2、根节点的颜色是黑色。

3、如果一个节点的颜色是红色，则该节点的左右孩子节点都是黑色。

4、对于每个结点，从该结点到其所有后代叶结点的简单路径上，均 包含相同数目的黑色结点。

5、每个叶子节点（这里的叶子节点指的是null节点）的颜色都是黑色的。

二、操作 

插入

插入一个新节点之后，会遇到几种情况，需要我们自己对红黑树进行调整，来保证其性质的正确。

新插入节点的颜色为红色。如果为黑色的话，性质4可能会不满足，相较于性质3来说，调整起来会比较麻烦。

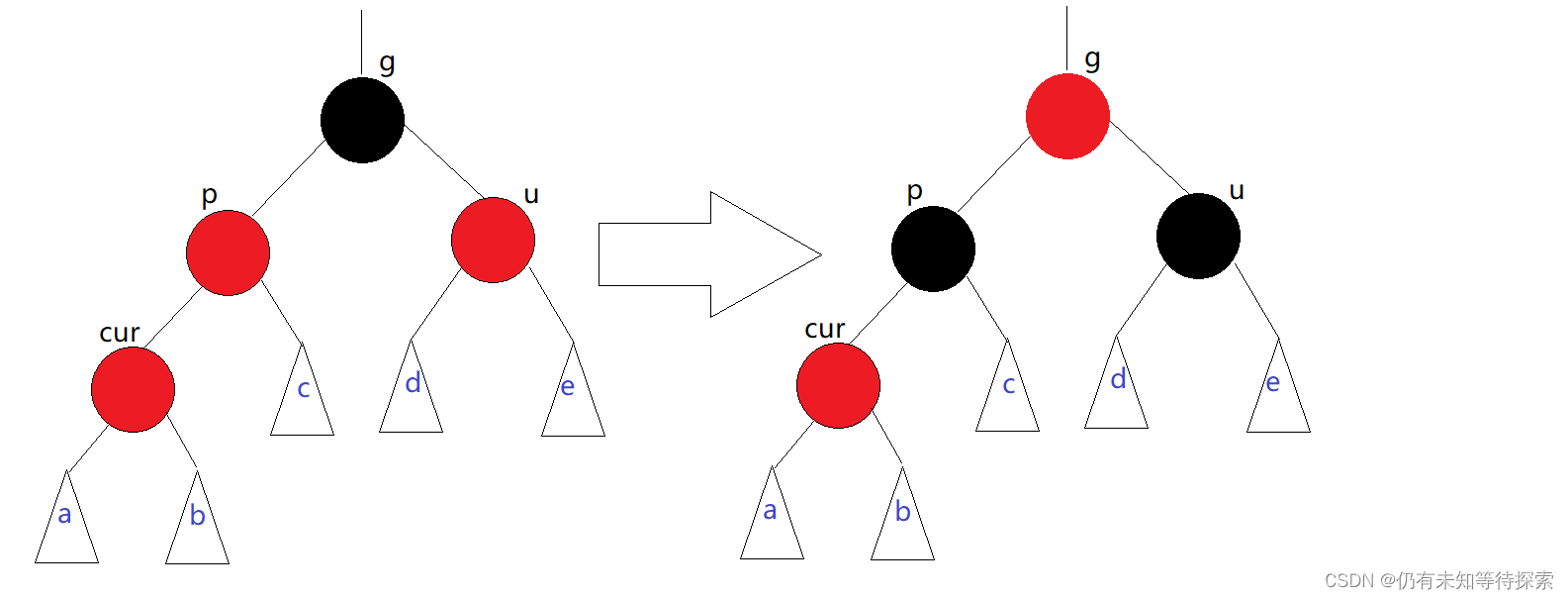
情况一：cur为红、p为红、g为黑，如果u存在且为红

步骤：

1. 将 p、u 变成黑色，g 变成红色。
2. 如果 g 为整个树的根节点，则将 g 变成黑色。
3. 如果 g 不是根节点，且双亲结点为红色的话，继续向上进行变换。
4. 如果 g 不是根节点，且双亲结点为黑色的话，则结束。

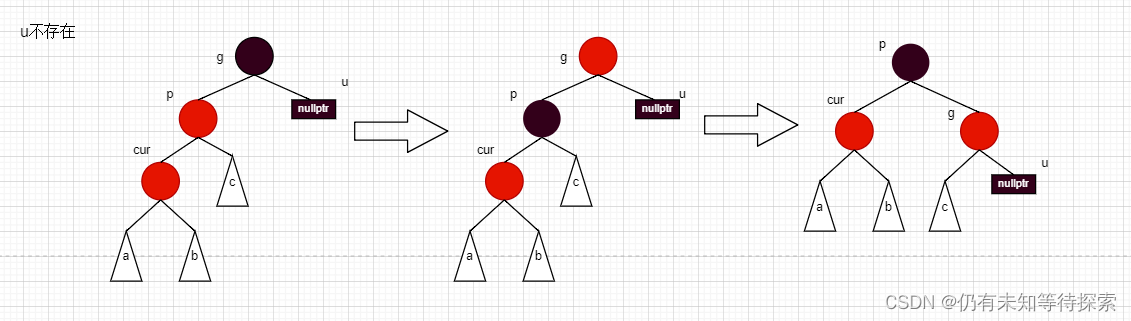
情况二：cur为红、p为红、g为黑，如果u不存在或者u存在且为黑 

对于这个情况二，还有两种不同的情况。注：p 节点一定是 cur 节点的双亲结点。

情况a：cur 为 p 的左孩子，p 为 g 的左孩子。

情况b：cur 为 p 的右孩子、p 为 g 的右孩子。

情况a步骤：

1. 将 p 变成黑色，g 变成红色。
2. 以 g 为旋转点，进行右单旋。

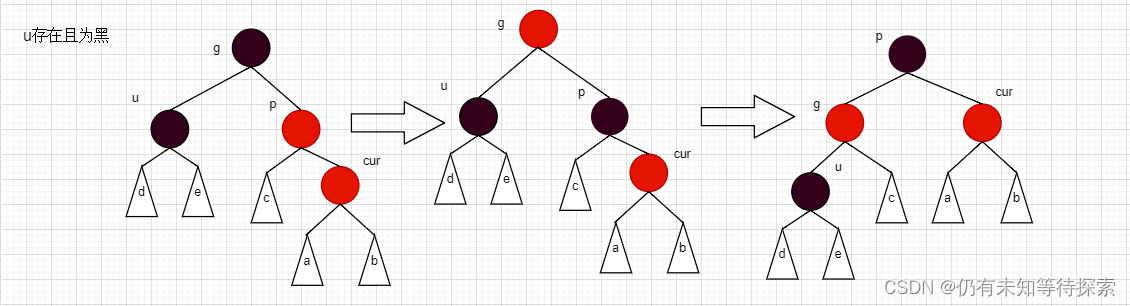
情况b步骤：

1. 将 p 变成黑色，g 变成红色。
2. 然后以 g 为旋转点，进行左单旋。

另外一种情况，u 不存在，就需要自己去琢磨咯。

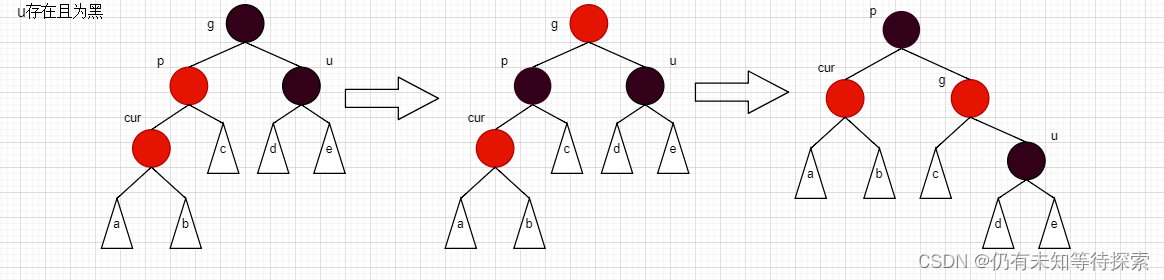
情况三：cur为红、p为红、g为黑，如果u不存在或者u存在且为黑 

情况三是情况二的补充。对于情况二，我们只讲了上述的两种情况。剩余的情况则在这里进行解释。

情况a：cur 为 p 的左孩子，p 为 g 的右孩子。

情况b：cur 为 p 的右孩子、p 为 g 的左孩子。

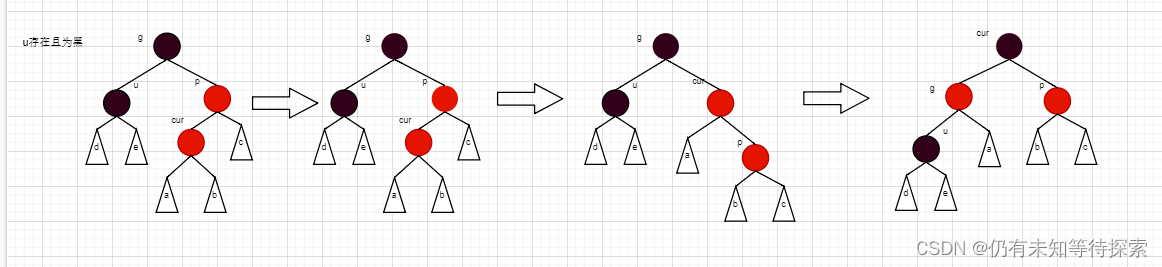
对于上述情况，想必大概也能猜测出来，这种情况要对红黑树进行双旋处理了。这里仅对情况a 且 u 存在进行画图分析。

步骤：

1. 先以 p 为旋转点进行右单旋，然后再以 g 为旋转点进行左单旋。
2. 然后将 cur 变成黑色，g 变成红色。

 三、总代码

#include <iostream>
#include <assert.h>
#include <vector>
using namespace std;

enum color
{
	Red,
	Black
};
template <class K, class V>
struct RBTreeNode
{
	typedef pair<K, V> PKV;

	RBTreeNode(const PKV& e = PKV())
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_col(Red)
		,_val(e)
	{}

	struct RBTreeNode<K, V>* _left;
	struct RBTreeNode<K, V>* _right;
	struct RBTreeNode<K, V>* _parent;
	int _col;
	PKV _val;
};

template<class K, class V>
class RBTree
{
public:
	typedef RBTreeNode<K, V> node;
	typedef pair<K, V> PKV;

	RBTree()
		:_root(nullptr)
	{}

	void insert(const PKV& e)
	{
		// 根据二叉搜索树插入的方式进行插入
		node* cur = _root;
		node* parent = cur;

		while (cur)
		{
			parent = cur;
			if (cur->_val.first > e.first)
			{
				cur = cur->_left;
			}
			else
			{
				cur = cur->_right;
			}
		}
		cur = new node(e);
		if (parent == nullptr)
		{
			_root = cur;
		}
		else
		{
			if (parent->_val.first > cur->_val.first)
			{
				parent->_left = cur;
			}
			else
			{
				parent->_right = cur;
			}
			cur->_parent = parent;
		}

		// 更新，对于不同的情况，进行不同的调整
		// parent 为黑、不存在，结束
		node* p = parent;
		while (p && p->_col == Red)
		{
			node* g = p->_parent;
			
			if (g->_left == p)
			{
				node* u = g->_right;
				// 叔叔存在且为红
				if (u && u->_col == Red)
				{
					p->_col = u->_col = Black;
					g->_col = Red;

					// 继续往上处理
					cur = g;
					p = cur->_parent;
				}
				// 叔叔不存在且为黑
				else 
				{
					//    g
					//  p   u
					// c
					if (cur == p->_left)
					{
						// 右单旋
						RotateR(g);

						// 变色
						g->_col = Red;
						p->_col = Black;

					}
					//    g
					//  p   u
					//    c
					else 
					{
						// 左右双旋
						RotateL(p);
						RotateR(g);

						// 变色
						cur->_col = Black;
						g->_col = Red;
					}
					// 叔叔不存在或者存在且为黑调整完，就不需要继续进行调整了
					break;
				}
			}
			else
			{
				node* u = g->_left;

				if (u && u->_col == Red)
				{
					p->_col = u->_col = Black;
					g->_col = Red;

					// 继续往上处理
					cur = g;
					p = cur->_parent;
				}
				else 
				{
					//    g
					//  u   p
					//        c
					if (cur == p->_right)
					{
						// 左单旋
						RotateL(g);

						// 变色
						g->_col = Red;
						p->_col = Black;

					}
					//    g
					//  u   p
					//    c
					else 
					{
						// 左右双旋
						RotateR(p);
						RotateL(g);

						// 变色
						cur->_col = Black;
						g->_col = Red;
					}
					// 叔叔不存在或者存在且为黑调整完，就不需要继续进行调整了
					break;
				}
			}
			
		}
		
		_root->_col = Black;
	}
	void inorder()
	{
		_inorder(_root);
	}
private:
	void _inorder(node* root)
	{
		if (root == nullptr) return;

		_inorder(root->_left);
		cout << root->_val.first << " ";
		_inorder(root->_right);
	}
	void RotateR(node* parent)
	{
		node* subl = parent->_left;
		node* sublr = subl->_right;

		node* grandfather = parent->_parent;

		parent->_left = sublr;
		if (sublr)
		{
			sublr->_parent = parent;
		}

		subl->_right = parent;
		parent->_parent = subl;

		subl ->_parent = grandfather;

		if (_root == parent)
		{
			if (grandfather->_left == parent)
			{
				grandfather->_left = subl;
			}
			else
			{
				grandfather->_right = subl;
			}
		}
		else
		{
			_root = subl;
		}
	}
	void RotateL(node* parent)
	{
		node* subr = parent->_right;
		node* subrl = subr->_left;

		node* grandfather = parent->_parent;

		parent->_right = subrl;
		if (subrl)
		{
			subrl->_parent = parent;
		}

		subr->_left = parent;
		parent->_parent = subr;

		subr ->_parent = grandfather;

		if (_root != parent)
		{
			if (grandfather->_left == parent)
			{
				grandfather->_left = subr;
			}
			else
			{
				grandfather->_right = subr;
			}
		}
		else
		{
			_root = subr;
		}
	}

protected:
	node* _root;
};